Случай нескольких функций

Соответствующий функционал имеет вид

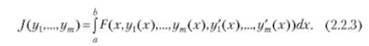
Относительно функций У) = У](х),] 1,2,...," предполагается, что все они заданы и непрерывно дифференцируемы на одном и том же промежутке [а, Ь], причем на концах этого промежутка у^а)-А^у^(Ь) для ^сех } = ,2,...,т. Обозначим множество таких функций через Ш'". Введем вектор-функцию у(х)=(у(х),„.1ут(х)). В этом случае простейшая задача вариационного исчисления состоит в отыскании вектор функции у(х) е Уту для которой функционал Лу) принимал бы наименьшее для всех у е V/'" значение.

Аналогом уравнения Эйлера здесь будет система дифференциальных уравнений

с соответствующими краевыми условиями yj(a) = Aj, Uj(b) Bj. Естественно, предполагается существование и непрерывность всех входящих в (2.2.4) производных. Подчеркнем еще раз, что условия (2.2.4) являются лишь необходимыми, но отнюдь не достаточными для того, чтобы соответствующие решения у(х) системы (2.2.4) были экстремалями функционала (2.2.3). Для проверки "экстремальности" соответствующих решений требуется дополнительное исследование (эта проблема аналогична задаче отыскания точек экстремума "обычной" функции в математическом анализе).

У. Гамильтон обратил внимание на следующее замечательное следствие вышеизложенной задачи, которое впоследствии дало толчок к развитию так называемых вариационных принципов механики. Рассмотрим находящуюся под действием потенциальных сил систему материальных точек с голономными (геометрическими) связями. Пусть обобщенные координаты системы будут о,, q2, q„; L = L(t, о,, qiv qv...,q„) — соответствующая функция Лагранжа. Здесь, как обычно, t — время, qj = qj(t), q} = ^"У/О. j 1.2,п = Т - П,

где Т— кинетическая, а П — потенциальная энергия системы. Как известно, кинетическая энергия 7'является квадратичной функцией обобщенных скоростей qj с коэффициентами, зависящими от времени и обобщенных координат, а потенциальная энергия П — функцией времени и обобщенных координат q^ Уравнения Лагранжа второго рода для такой системы имеют вид

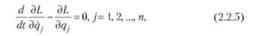
что, с точностью до обозначений, совпадает с системой уравнений Эйлера (2.2.4). Соответствующий функционал, порождающий систему уравнений (2.2.5), имеет вид

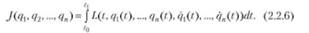
Функционал (2.2.6) называется действием по Гамильтону. Здесь наборы переменных с$ = ц$0),а% <72(го)> ~

= "Д*о) и <А=4(к)><А Я(Ч)>-Пп=Яп(Ч) залают начальное (¿ = ¿0) и конечное (¿ = ¿1) состояния системы соответственно.

Принцип Гамильтона (принцип наименьшего, или стационарного, действия) гласит, что голономная система материальных точек, находящаяся под действием потенциальных сил, движется таким образом, что функционал действия (2.2.6) достигает наименьшего (точнее, стационарного) значения на истинных траекториях материальных точек, составляющих систему.

Таким образом, принцип Гамильтона может быть положен в основу классической механики, а задачу решения уравнений Лагранжа (2.2.5) (соответственно, уравнений Эйлера (2.2.4)) можно заменить задачей непосредственного нахождения стационарных точек функционала (2.2.6) (соответственно, функционала (2.2.3)). Методы, позволяющие это делать, носят название прямых методов вариационного исчисления. К таким методам, в частности, относится ряд численных методов вариационного исчисления.

Аналогия простейшей задачи вариационного исчисления с классической механикой прослеживается и в гак называемой задаче Лагранжа, или задаче нахождения условного экстремума функционала (2.2.3). Поставим задачу отыскания экстремума функционала (2.2.3) при дополнительном условии у(1)е, /се[а, Ь], где I — гладкое многообразие, определяемое £ условиями

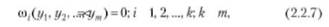
где все соу(г/,, //2. = 0 — непрерывно дифференцируемые функции, и матрица Якоби этих функций имеет ранг, равный к (по числу функций ©,):

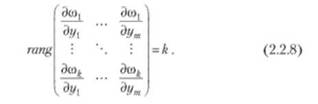
Условие (2.2.7) позволяет из системы уравнений (2.2.5) выделить п = т £-независимых переменных г/7 , 5 = 1,2,и, через которые могут быть выражены остальные & переменных г/,-. Если обозначить эти независимые переменные у-} через <7Х,$ = 1,2,..., п, то наша задача сведется к простейшей ("безусловной") задаче вариационного исчисления для функционала типа (2.2.6). Ясно, что все стационарные точки соответствующего функционала будут удовлетворять условию (2.2.7)'.

Частным случаем является так называемая задача о геодезических: среди всех гладких кривых, лежащих на многообразии X и соединяющих две заданные точки, найти кривую наименьшей длины. Такие кривые называются геодезическими. В частности, эта задача тесно связана с задачей о распространении света в общей теории относительности.