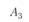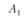Симплекс-метод с искусственным базисом (М-метод)
Применяется в тех случаях, когда затруднительно найти первоначальный опорный план исходной задачи ЛП, записанной в канонической форме.
М-метод заключается в применении правил симплекс- метода к так называемой М-задаче. Она получается из исходной добавлением к левой части системы уравнений в канонической форме исходной ЗЛП таких искусственных единичных векторов с соответствующими неотрицательными искусственными переменными, чтобы вновь полученная матрица содержала систему единичных линейно-независимых векторов. В линейную форму исходной задачи добавляется в случае ее максимизации слагаемое, представляющее собой произведение числа (-М) на сумму искусственных переменных, где М – достаточно большое положительное число.
В полученной задаче первоначальный опорный план очевиден. При применении к этой задаче симплекс-метода оценки 
теперь будет зависеть "от буквы М". Для сравнения оценок нужно помнить, что М – достаточно большое положительное число, поэтому из базиса будут выводиться в первую очередь искусственные переменные.
В процессе решения М-задачи следует вычеркивать в симплекс-таблице искусственные векторы по мере их выхода из базиса. Если все искусственные векторы вышли из базиса, то получаем исходную задачу. Если оптимальное решение М-задачи содержит искусственные векторы или М-задача неразрешима, то исходная задача также неразрешима.
Путем преобразований число вводимых переменных, составляющих искусственный базис, может быть уменьшено до одной.
Пример 2.8. Найти максимум целевой функции: 
при условиях
Решение. Матрица условий содержит только один единичный вектор, добавим еще один искусственный вектор (искусственную неотрицательную переменную 
в первое ограничение):
Получим следующую М-задачу: найти максимум целевой функции 
при условиях
М-задачу решаем симплекс-методом. Начальный опорный план (0, 0, 6, 8), решение проводим в симплекс-таблицах (табл. 2.3).
В начальной таблице наименьшее 
соответствует вектору 
– он вводится в базис, а искусственный вектор
из базиса выводится, так как ему отвечает наименьшее Q. Столбец, соответствующий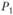
, из дальнейших симплексных таблиц вычеркивается.
Таблица 2.3
Решение М-задачи в симплекс-таблицах
|
Номер симплекс- таблицы |
Базис |
|
План В |
3 |
2 |
1 |
-M |
Q |
|
|
|
|
|
|||||
|
|
-М |
8 |
2 |
1 |
0 |
1 |
4 |
|
|
0 |
|
1 |
6 |
1 |
1 |
1 |
0 |
6 |
|
|
- |
-8М+6 |
-2М-2 |
-М-1 |
0 |
0 |
- |
|
|
|
3 |
4 |
1 |
0,5 |
0 |
|
||
|
1 |
|
1 |
2 |
0 |
0,5 |
1 |
||
|
|
- |
14 |
0 |
0 |
0 |
Полученный новый опорный план является опорным планом исходной задачи. Для него все 
, поэтому он является и оптимальным. Таким образом, получен оптимальный план исходной задачи (4, 0, 2) и максимальное значение целевой функции 
Пример 2.9. Решить ЗЛП:
Решение. Приведем ЗЛП к каноническому виду, перейдя к задаче "на максимум":
Для нахождения опорного плана переходим к М-задаче:
Дальнейшее решение проводим в симплекс-таблицах (табл. 2.4).
Таблица 2.4
Решение ЗЛП М-методом
|
Номер симплекс-таблицы |
Базис |
|
В |
-10 |
5 |
0 |
0 |
0 |
-M |
-M |
Q |
|
|
|
|
|
|
|
|
|||||
|
0 |
|
–М |
3 |
2 |
-1 |
-1 |
0 |
0 |
1 |
0 |
3/2 |
|
|
–М |
2 |
1 |
1 |
0 |
-1 |
0 |
0 |
1 |
2 |
|
|
|
0 |
1 |
-1 |
-2 |
0 |
0 |
1 |
0 |
0 |
||
|
– |
|
- |
-5М |
-3М+ + 10 |
-5 |
M |
М |
0 |
0 |
0 |
– |
|
|
-10 |
3/2 |
1 |
-1/2 |
-1/2 |
0 |
0 |
|
0 |
– |
|
|
I |
|
-M |
1/2 |
0 |
3/2 |
1/2 |
-1 |
0 |
1 |
1/3 |
|
|
|
0 |
5/2 |
0 |
-5/2 |
-1/2 |
0 |
1 |
0 |
– |
||
|
– |
|
- |
-М/ 2- -15 |
0 |
-3М/2 |
-М/2+ +5 |
M |
0 |
0 |
– |
|
|
|
-10 |
5/3 |
1 |
0 |
-1/3 |
-1/3 |
0 |
|
|
– |
|
|
II |
|
5 |
1/3 |
0 |
1 |
1/3 |
-2/3 |
0 |
– |
||
|
|
0 |
10/3 |
0 |
0 |
0 |
-5/3 |
1 |
– |
|||
|
– |
|
– |
-15 |
0 |
0 |
5 |
0 |
0 |
– |
В симплекс-таблице II получен опорный план исходной ЗЛП; поскольку все симплекс-разности 
, то этот план является и оптимальным, т.е.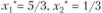 
(исходные переменные), 
(дополнительные переменные), при этом 
.
При рассмотрении графического метода выделялись три особых случая решения ЗЛП. В симплекс-методе эти случаи определяются следующим образом.
1. Если найден оптимальный план и оценки всех свободных переменных строго больше нуля, то оптимальный план является единственным; если оценки некоторых свободных переменных в оптимальном плане равны нулю, то этот план будет неединственным, так как ввод этих переменных в базис не нарушает критерия оптимальности и не меняет оптимальное значение целевой функции. В соответствии с этим оптимальный план в табл. 2.2 является единственным, а в табл. 2.3 и 2.4 – неединственным (первый особый случай).
2. Если в процессе решения ЗЛП М-методом искусственные переменные не выводятся из базиса, это является свидетельством того, что область определения исходной ЗЛП является пустым множеством: в этом случае ЗЛП не имеет решения ввиду противоречивости системы ограничений (второй особый случай).
3. Если в направляющем столбце все элементы aik неположительны (см. 2.23), то это свидетельствует о незамкнутости области определения ЗЛП; в этом случае ЗЛП не имеет решения ввиду неограниченности целевой функции (третий особый случай).
Для автоматизации решения задач линейного программирования могут быть использованы стандартные офисные средства Microsoft Excel – надстройка Поиск решения, использующая симплексный метод (линейная оптимизация с помощью надстройки Поиск решения подробно рассмотрена, например, в литературе[1]).
Однако для корректного и эффективного использования программных средств необходимо знать основы линейного программирования, изложенные выше в данной главе.