Сетевые модели в географии

Надо заниматься сетью как таковой, а не тем, к чему она относится.

Л. Витгенштейн

Разнообразные линейные формы традиционно применяют в области физической и экономической географии: для исследования рек, железных дорог, административных границ с точки зрения основных геометрических свойств. Исследуем их для общего класса "географических сетей". Соотношения между сетями представлены на рис. 11.3.

Геометрия трасс. Первый (простейший) класс географической сети – отдельная линия, или трасса. Рассмотрим простые задачи о трассах оптимальных путей и форме блуждающих путей. В обоих случаях подход, рассматриваемый П. Хаггетом, скорее иллюстративный, чем строго аналитический (рис. 11.4).

Оптимальные пути (задача о прокладке трассы). Элементарная основополагающая посылка, что прямая является кратчайшим расстоянием между двумя точками на плоскости, затушевывает реальную сложность задач о трассах путей, соединяющих точки.

Простая задача о соединении трех точек на плоскости кратчайшим путем занимала еще геометров Древней Греции. Например, возникал вопрос о том, как проложить кратчайшую трассу между двумя приречными деревнями таким образом, чтобы по пути можно было набрать воды, было получено два решения: 1) для прямолинейного русла – это путь светового луча, отраженного зеркалом; 2) для русла неправильной формы положение оптимального пункта забора воды – это место, где самый маленький эллипс, фокусами которого будут обе деревни, коснется берега реки.

Вопрос о прокладке пути через систему точек рассматривался также в связи со строительством железных дорог. Практическая задача, решаемая при этом, состоит в том, чтобы добиться оптимального соотношения между суммарной длиной пути (проектируемой железной дороги) и числом соединенных им точек (городов).

При исследовании трасс решаются следующие задачи:

– определение кратчайшего маршрута;

– отыскание пути максимального потока;

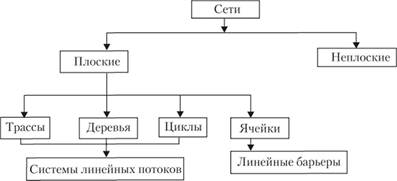
Рис. 11.3. Топологическая классификация сетей

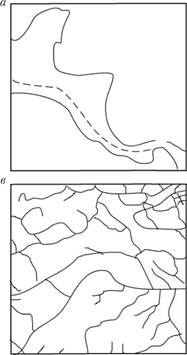
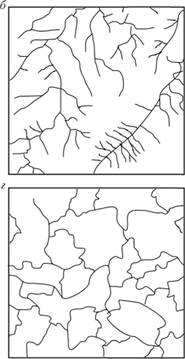
Рис. 11.4. Географические примеры сетей разных топологических классов:

а – трассы – трассы автомагистралей; б – деревья – русла водотоков; в – циклы – дорожная сеть; г – ячейки – административные подразделения

– нахождение пути, обеспечивающего минимальные издержки в пути.

Блуждающие пути (анализ формы). Дороги или русла рек являются примерами изменчивых, или блуждающих, путей, которые как бы "избегают" прямой трассы от места их видимого начала к месту видимого назначения.

Афоризм "природа избегает прямых путей" мало помогает объяснению меандрирующей формы рек. Многочисленные пики в полученных спектрах меандров (устойчивых колебаний), по мнению Спайджата, позволяют сделать вывод о том, что "реку, подобно музыкальному инструменту, можно рассматривать как резонирующую колебательную систему, однако с тем существенным отличием, что колебания отражают здесь случайную периодичность пространственного, а не временного характера". Колебания системы требуют энергии, и ясно, что для рек главным ее источником будет потенциал, обусловленный высотой водотока над базисом эрозии. Коль скоро в речной системе возникает устойчивое колебание, оно, по-видимому, само поддерживает свое существование, а такие факторы, как подмыв берегов, способствуют по принципу обратной связи возвращению энергии колебаний в систему.

Геометрия деревьев. Второй класс географических сетей образуют древовидные структуры. Они представляют собой множество связанных линий без замкнутых контуров и в топологии носят название связных графов без циклов (рис. 11.5, а – д), или просто деревьев. При их исследовании делается акцент не на трассе и форме, а на структуре и росте.

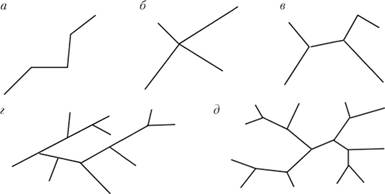
Рис. 11.5. Разные геометрические формы топологических деревьев

Геометрия сетей с замкнутыми контурами. Третий класс географических сетей образуют системы с замкнутыми контурами, или циклами. Самые распространенные циклические системы образуют запутанные сети безрельсовых и железных дорог.

Геометрия ячеек. Четвертый класс географических сетей значительно отличаются от остальных. Если в рассмотренных выше сетях потоки различной сложности перемещались вдоль линий, то ячеистую сеть образуют барьерные линии, пересекаемые потоками в поперечном направлении. В природе примером ячеистых сетей может служить замкнутый контур водоразделов, ограничивающий бассейн стока, а в географии человека – замкнутые границы политико-административных подразделений.

Некоторые особенности моделей стационарных ячеистых сетей, например сочленение трех ребер у вершины или одинаковый размер ячеек, трудно обнаружить в реальной действительности. Так, при анализе сети торговых точек географическая поверхность с обычными мерами расстояния преобразуется в поверхность доходов, где расстояния измеряются с учетом доходов населения. Впрочем, при построении стационарных моделей возникает еще более серьезное затруднение, так как в их основу заложено наличие состояния равновесия и нс учитываются отдельные этапы его достижения, т.е. таким образом модели отражают как бы мгновенно сложившуюся ситуацию. Но такой подход часто оказывается бесполезным, так как ячеистые сети обычно складываются в ходе итеративного, поэтапно повторяющегося процесса и границы, сложившиеся на ранних стадиях развития, не обязательно соответствуют условиям, возникшим позднее. Фактически время релаксации многих географических систем так велико, что однажды установленные границы затем уже и сами по себе образуют важные опорные линии, поэтому новые рубежи проводятся с учетом этих ранее установленных границ.

Некоторые идеи, весьма полезные для моделирования итеративного процесса деления ячеек, можно извлечь из детальных исследований, посвященных физике процессов разрыва в твердых телах. Аналогия заключается в следующем соображении:

1) можно ожидать, что в плоской пластине частотное распределение структурных дефектов материала (ослабленные точки, линии и участки) асимметрично, т.е. крупные дефекты будут встречаться реже, а мелкие – чаще. Если мы допустим, что дефекты размещены в материале случайно, то крупные дефекты в среднем будут разделены большим расстоянием, чем мелкие;

2) каждая трещина на нашей условной пластине приведет к появлению вокруг нее буферной зоны определенной ширины. В пределах этой зоны образование новой трещины маловероятно, так как предыдущий разрыв привел к ослаблению упругих напряжений поблизости от него. Кроме того, прочность поверхности, не затронутой разрывом, увеличивается благодаря исчезновению наиболее слабых мест.

Преобразование сетей опирается на алгоритм их классификации, состоящий из ряда этапов (стадий).

1. Установление полюсов. В любой циклической сети можно выделить их и классифицировать эти вершины по значениям какого-либо параметра, начиная от самого большого полюса и кончая наименьшим.

2. Обособление полярной сети. При анализе циклических сетей понятие "полярная сеть" аналогично понятию "бассейн стока". При этом плоские графы отождествляют с понятием об областях Дирихле на плоскости. Области Дирихле (их называют также полигонами Вороного и полигонами Тиссена) представляют собой сопряженные с некой системой узлов многоугольники, внутри которых все точки находятся ближе к узлу данного многоугольника, чем к любому другому узлу.

3. Определение иерархии сетей. Можно считать, что небольшие бассейны стока математически сгруппируются в более крупные бассейны. Такого рода "гнездование" наблюдается и в системе транспортных потоков.

4. Расчленение циклов.

5. Классификация трасс.

Основной вопрос всегда стоит о структуре сети, т.е. о конфигурации образующих ее линий, их взаимосвязях и зависимости от внешних сил, воздействующих на сеть.