Ряды распределения маркетинговой информации

При анализе маркетинговой информации различают два вида рядов распределения: атрибутивный и вариационный.

Под атрибутивным рядом понимается ряд распределения по атрибутивному признаку, не имеющему количественной меры, например, пол потребителя, социальное положение, товар. Пример атрибутивного ряда распределения представлен в табл. 5.12.

Таблица 5.12

Группировка товаров в магазине по признаку "ассортимент"

Категория	Частота	Частость, %
Товар 1	65	73,86
Товар 2	8	9,09
Товар 3	12	13,63
Товар 4	3	3,42
Товар 5	88	100

Частота — это количество элементов совокупности, которые имеют данное значение признака, а частость — отношение частоты к общему количеству исследуемых элементов, т.е. к объему совокупности.

Вариационный ряд (вариация — колеблемость) — это ранжированный (упорядоченный) в порядке возрастания или убывания ряд статистических частот (частостей); подразделяется на ранжированный, дискретный и интервальный ряды. Ранжированный ряд — это распределение отдельных единиц совокупности в порядке возрастания или убывания исследуемого признака. Дискретный ряд — это ряд, в основу построения которого положены дискретные признаки (табл. 5.13). В интервальном ряду значение признака представляется в виде интервалов (табл. 5.14).

Таблица 5.13

Дискретный ряд распределения качества продаваемого товара

Оценка качества	Частота	Частость, %
Отличное	7	15,9
Хорошее	24	54,54
Удовлетворительное	12	27,27
Неудовлетворительное	1	2,29
Итого	44	100

Таблица 5.14

Интервальный ряд распределения цен на товар в регионе

Цена товара, руб.	Частота	Частость, %
1200-1250	37	31,89
1250-1300	58	50
1300-1350	21	18,11
Итого	116	100

В качестве основного показателя интервала используется середина интервала, вычисляемая по формуле

Для графического изображения интервальных вариационных рядов применяется гистограмма (рис. 5.4). Она строиться так: на оси абсцисс откладываются равные отрезки, которые в принятом масштабе соответствуют величине интервалов вариационного ряда. На отрезках строят прямоугольники, площади которых пропорциональны частотам интервала.

Рис. 5.4. Гистограмма

Гистограмма может быть преобразована в полигон распределения, если середины верхних сторон прямоугольников соединяются отрезками прямых. Две крайние точки прямоугольников замыкаются по оси абсцисс на середины интервалов, в которых частоты равны нулю.

В целях наглядного представления временного ряда используются линейные диаграммы (полигон, кумулята), на которых ряд точек соединен непрерывной линией (рис. 5.5).

Полигон — это ломаная кривая, строящаяся в прямоугольной системе координат, когда по оси X откладывается значение признака, а по оси У — частоты (см. рис. 5.5, а). Кумулята — ломаная кривая, строящаяся в декартовой системе координат, когда по оси X откладываются значения признака, а по оси Y — накопленные частоты (см. рис. 5.5, б). При этом для дискретных рядов на оси X откладываются сами значения признаков, а для интервальных — середины интервалов.

Иногда при исследовании вариационных рядов маркетологов интересует параллельное изменение нарастающих долей единиц совокупности и нарастающих долей значений признака в общем объеме. Такая задача возникает при изучении концентрации какого-либо признака в тех или иных группах совокупности. В этих случаях для анализа концентрации строят так называемую кривую Лоренца. По оси X откладываются накопленные частости, характеризующие распределение единиц совокупности, по оси У — кумулятивные доли значений признака в общем объеме. Чем больше кривая Лоренца отклоняется от диагонали, тем выше степень неравномерности распределения признака в совокупности. Эта степень неравномерности выражается в виде площади, заключенной между диагональю квадрата и кривой Лоренца. Например, по данным табл. 5.15 строится кривая Лоренца (см. рис. 5.5, в).

Рис. 5.5. Виды графических изображений вариационного ряда исследуемых значений:

а — полигон распределения; б — кумулятивная кривая; в — график Лоренца

Таблица 5.15

Расчетная таблица

Цена товара	Середина интервала хi	Глубина ассортимента mi	Частота fi	Частость pi, %		Накопления qi	Кумулятивные доли qi • 100%
120-125	122,5	3	17	22,97	0,11	0,11	11
125-130	127,5	8	21	28,37	0,3	0,41	41
130-135	132,5	15	36	48,66	0,59	1,0	100
Итого	-	26	74	100	1,0	-	-

Вариационные ряды имеют графическое представление в виде частотной, линейчатой и круговой диаграмм.

Рассмотрим средние величины в статистическом понимании маркетинговых исследований. Это обобщающие показатели совокупности однотипных явлений по какому-либо количественному признаку.

Цель определения средних величин — ослабить влияние случайных факторов на изучаемый показатель; получить сводный показатель, описывающий данную совокупность в целом.

Средние величины подразделяют на математические и структурные. К математическим средним относят среднеарифметические, среднегеометрические и гармонические средние; к структурным — моду и медиану.

Среднеарифметическая простая равна простой сумме значений усредняемого признака, деленной на общее число этих значений:

где Xi — варианты значений признака; п — число единиц совокупности.

Среднеарифметическая взвешенная исчисляется для сгруппированных данных по формуле

где f — частоты;

где N — объем совокупности.

Пусть, например, имеются данные покупательной способности домохозяек дома N (табл. 5.16).

Таблица 5.16

Покупательная способность домохозяек

Месячный объем покупок Хi, тыс. руб.	Число домохозяек fi	fiXi
1,10	2	2,20
1,30	6	7,80
1,60	16	25,60
1,90	12	22,80
2,20	14	30,80
Итого	50	89,20

Средняя покупательная способность этих домохозяек составляет:

Среднее геометрическое определяют по формуле

Средняя геометрическая применяется в тех случаях, когда индивидуальные значения признака представляют собой относительные величины динамики, построенные в виде цепных величин, как отношение к предыдущему уровню каждого уровня в ряду динамики, т.е. характеризует средний коэффициент роста. Этот показатель используется при расчете индексов, определения средних темпов изменения в рядах динамики, а также в рядах распределения.

Средняя гармоническая величина обратна средней арифметической из обратных значений признака:

где Мi — объемное значение признака; Xi — его варианты.

Средняя гармоническая применяется в тех случаях, когда известны варианты признака, его объемное значение, но не известны частоты.

Пусть, например, известна средняя цена товара на трех локальных рынках (табл. 5.17).

Таблица 5.17

Расчетная таблица

Номер рынка	Стоимость 1 м2 площади	Цена единицы товара, тыс. руб.
1	200	2,0
2	460	2,3
3	110	2,2

Средняя цена товара по трем рынкам составит:

Хi= (200 + 460+ 110) / (200 / 2,0 + 460 /2,3 + 110/2,2) = 770 / / 345,6 = 2,228 тыс. руб.

Мода — наиболее типичное, чаще всего встречаемое значение признака. В случаях интервальных рядов с неравными интервалами модальным интервалом считается интервал с наибольшей плотностью, а при равных интервалах — интервал с наибольшей частотой. При неравных интервалах расчет моды выполняется с помощью табл. 5.18.

Таблица 5.18

Образец построения

Интервал

группировки

Интервальная разность

Частота

Частость

Плотность

Δi

. ..

Значение моды в этом случае определяют по формуле

где Хн — значение нижней границы модального интервала; а1, а2 — параметры, определяемые следующим образом:

где X1, Х2, X3 — границы трех интервалов, полученные после приведения нижней границы модального интервала к нулю (путем вычитания ее фактической величины из всех границ фактических, интервалов; при этом X1 — нижняя граница предмодального интервала; Х2 — верхняя граница модального интервала; Х3 — верхняя граница постмодального интервала); φ1, φ2, φ3 — частости этих трех интервалов.

Моду интервального вариационного ряда с равными интервалами рассчитывают но формуле

где Хm — нижняя граница модального интервала; im — величина модального интервала; fт — частота модального интервала; fm-1 — частота предмодального интервала; fт+1 — частота послемодального интервала.

Медиана — значение варьирующего признака, приходящееся на середину ранжированной совокупности. При исчислении медианы интервального ряда сначала находят интервал, содержащий медиану. Медианному интервалу соответствует первый из интервалов, для которых накопленная сумма частот превышает половину общей совокупности наблюдений. Внутри найденного интервала расчет медианы производят по следующей формуле:

где Хтн нижняя граница медианного интервала; di — величина интервала разбиения; N — число наблюдений; Fi-1 — накопленная частота интервала; fi — частота медианного интервала.

Медиана делит вариационный ряд пополам по вероятности. Определяют еще квартили, которые делят вариационный ряд на четыре равновеликие по вероятности части, и децили, делящие ряд на 10 равновеликих но вероятности частей.

Различие индивидуальных значений признака внутри изучаемой совокупности называется вариацией признака. Рассмотрим показатели вариации (колеблемости) признака.

Показателями линейной вариации выступают размах, среднее линейное отклонение, среднее относительное отклонение. К показателям квадратического отклонения относятся сумма квадратов отклонений, дисперсия, среднеквадратическое отклонение, коэффициент вариации.

Для характеристики совокупностей и исчисленных средних величин важно знать, какая вариация изучаемого признака скрывается за средними. Основа показателей общая — оценка отклонений значений показателей элементов совокупности от средней.

Размах представляет собой разность между максимальной и минимальной величиной признака:

Среднее линейное отклонение определяют по формуле

где xi — значение показателя; X — среднее арифметическое значение.

Среднее линейное отклонение в "чистом" виде для анализа не применяют, используя как составляющую для вычисления среднего относительного отклонения

Сумма квадратов отклонений является основой для вычисления относительного показателя — дисперсии•.

или для интервальных рядов

Среднее квадратическое отклонение находят по следующей формуле: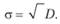

Среднеквадратическое отклонение показывает, как расположена основная масса единиц совокупности относительно среднеарифметической. В соответствии с теоремой П. Л. Чебышева независимо от формы распределения 75% значений признака попадут в интервал X ± 2 σ, а по крайней мере 89% всех значений попадут в интервал X ± 3 σ.

Коэффициент вариации определяют по формуле

По величине коэффициента вариации можно судить о степени вариации (колеблемости) признаков совокупности. Чем больше его величина, тем больше разброс значений вокруг средней, тем менее однородна совокупность по своему составу и тем менее представительна средняя. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений близких к нормальному). Коэффициент вариации важен и в тех случаях, когда нужно сравнивать средние квадратические отклонения, выраженные в разных единицах измерения.

Для удобства расчетов представлена технология заполнения (табл. 5.19).

Таблица 5.19

Исходная таблица

Интервал группировки	Частота	Центр интервала	Произведение	Произведение
i	fi	xi	fixi	fi2xi

Средняя ошибка выборки маркетинговых исследований показывает среднюю величину всех возможных расхождений выборочной и генеральной средней. Величина средней квадратической стандартной ошибки простой случайной повторной выборки может быть определена по формуле

Предельная ошибка выборки рассчитывается по формуле

где t — коэффициент доверия, зависящий от вероятности Р.

Значения t при заданной вероятности Р определяются по таблице значений функции φ(ί), которая выражается интегральной формулой Лапласа и отражает зависимость между t и вероятностью Р.

В оценке вариационного ряда данных рынка чаще других рассчитываются следующие показатели:

• абсолютные цепные приросты

• абсолютные базисные приросты

где ув — значение показателя, принятое за базисное;

• темпы роста цепные

темпы роста базисные

темпы прироста цепные

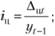
темны роста базисные

Сводной, обобщающей характеристикой интенсивности изменения уровней ряда динамики является средний темп роста, показывающий, во сколько раз в среднем за единицу времени изменился уровень ряда. Средний темп роста находится как знаменатель геометрической прогрессии:

Средний темп прироста вычисляют по формуле

Анализ динамики социально-экономических явлений следует проводить, используя все показатели. Пренебрежение каким-либо показателем приводит к неполному одностороннему анализу.