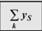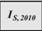Ретроспективный и прогнозный анализ

Ретроспективный анализ основан на изучении рядов динамики. Анализ динамических рядов позволяет получить информацию о значимых изменениях в динамике экономических показателей. Кроме того, такой анализ позволяет определить моменты времени, в которые произошли эти изменения. Изменчивость хозяйственной деятельности определяется целым рядом взаимосвязанных и взаимозависимых факторов. Поэтому при изучении динамического ряда выделяют четыре уровня факторов.

1. Долговременные факторы, формирующие основную тенденцию развития признака, или тренд (Т).

2. Циклические факторы (С), которые формируют колебания анализируемого признака, обусловленные действием циклов экономической природы более одного года.

3. Сезонные факторы (S), которые определяют колебания в течение календарного года, и такие колебания повторяются из года в год. Сезонные колебания связываются с ежегодными циклами.

4. Случайные факторы (ε), появление которых невозможно предвидеть, а степень воздействия сложно измерить из-за их кратковременности. Этот компонент ряда времени связан с рисками, сопровождающими хозяйственную деятельность, и поэтому является непредсказуемым.

Совершенно не обязательно, чтобы в процессе формирования значений временного ряда участвовали одновременно факторы всех четырех типов. В одних случаях значения временного ряда могут формироваться под воздействием факторов (Т), (S) и (ε), в других – под воздействием факторов (Т), (С) и (ε).

В экономическом анализе более востребованной является модель, выраженная функцией

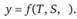
Взаимосвязь этих компонент выражается аддитивной (1) или мультипликативной (2) моделью:

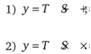
Аддитивная модель используется тогда, когда сезонные колебания значений изучаемых показателей являются относительно постоянными за период наблюдения. Мультипликативная модель характеризуется постоянством колебаний только по отношению к тренду.

Рассмотрим методы моделирования компонентов динамического ряда.

Выделение тренда может быть произведено методами механического или аналитического сглаживания. Наиболее распространенным методом механического сглаживания является метод скользящей средней.

Сглаживание ряда динамики с помощью скользящих средних заключается в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из такого же числа уровней ряда, начиная со второго, далее – с третьего и т.д. Период скользящей средней может быть четным и нечетным. Если принимается нечетный период, то скользящая относится к середине периода. Если для выравнивания ряда выбирается четный период, то дополнительно проводится центрирование, т.е. нахождение средней из средних для отнесения полученного уровня к определенной дате.

Так, скользящие средние с продолжительностью периода, равной трем, будут иметь вид:

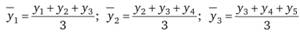и т.д.

Пример

Необходимо произвести сглаживание динамического ряда показателя объема продаж (млн руб.) методом скользящей средней.

Квартал	1	2	3	4	5	6	7	8	9	10	11	12
Объем продаж	9,7	9,9	11,4	12,9	14,9	12,1	11,0	9,8	7,9	8,2	9,9	12,0

Сглаживание с помощью трехквартальных скользящих средних:

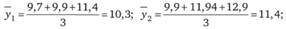
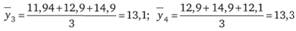и т.д.

Сглаживание с помощью четырехквартальных скользящих средних:

Поскольку для расчета был использован четный период (четыре квартала) производится центрирование данных:

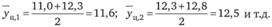
Результаты расчетов отражены в таблице.

Квартал	Объем продаж	Трехчленные скользящие средние	Четырехчленные скользящие средние
			нецентрированные	центрированные
1	9,7
2	9,9	10,3
3	11,4	11,4	11,0	11,6
4	12,9	13,1	12,3	12,5
5	14,9	13,3	12,8	12,7
6	12,1	12,7	12,7	12,3
7	11,0	11,0	11,9	11,0
8	9,8	9,6	10,2	9,7
9	7,9	8,6	9,2	9,0
10	8,2	8,7	8,9	9,2
11	9,9	10,0	9,5
12	12,0

С увеличением числа периодов скользящая средняя все более будет приближаться к прямой линии.

Целью аналитического сглаживания динамического ряда является определение аналитической или графической зависимости 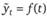при помощи регрессионного анализа. Функцию f(t) выбирают таким образом, чтобы она давала содержательное объяснение изучаемого процесса. При этом целесообразно воспользоваться сглаженными уровнями, в которых случайные колебания показателя погашены.

Для выделения тренда наиболее распространены следующие зависимости:

1) линейная форма тренда

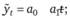
2) гиперболическая форма тренда

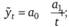
3) параболическая форма тренда

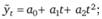
4) показательная форма тренда

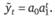
В аналитических исследованиях применяются и более сложные формы тренда, например полиномы третьей и четвертой степени, логистические и логарифмические зависимости, уравнение с применением рядов Фурье и другие.

(Системы нормальных уравнений для некоторых зависимостей и расчет параметров уравнений были рассмотрены в гл. 6.)

Пример

Требуется определить функции тренда объема продаж по данным предыдущего примера.

Построим линии тренда, используя линейную и параболическую зависимость. Для линейной формы тренда

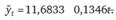
Для параболической формы тренда

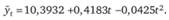
Для анализа сезонных колебаний можно использовать метод, сводящийся к расчету индексов сезонности, совокупность которых формирует сезонную волну:

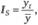
где 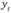– значение уровня ряда динамики, соответствующее интересующему нас интервалу времени;

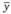– среднее значение уровней ряда динамики.

Пример

По данным приведенного выше примера необходимо вычислить индексы сезонности показателя.

Среднее значение 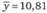. Результаты расчетов индексов сезонности представлены в таблице.

Месяц	1	2	3	4	5	6
	9,7	9,9	11,4	12,9	14,9	12,1
	0,90	0,91	1,05	1,19	1,38	1,12
Месяц	7	8	9	10	11	12
	11,0	9,8	7,9	8,2	9,9	12,0
	1,02	0,91	0,73	0,76	0,91	1,11

Результаты показывают, что пик сезонной волны приходится на пятый месяц года, а наибольший спад – на девятый месяц, что полностью совпадает с полученными ранее результатами. Эта информация может помочь руководству предприятия определить меры для сглаживания сезонных колебаний.

Изучение сезонных колебаний в пределах одного года не является надежным источником информации в силу влияния многочисленных случайных факторов на развитие хозяйственной деятельности. Более точную оценку дают индексы сезонности, рассчитанные по месячным данным за к лет. В этом случае индекс сезонности равен

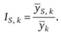
Представленные в формуле показатели рассчитываются следующим образом:

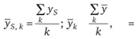
где 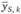– среднее значение уровня (сезона) за k лет;

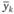– среднее значение средних уровней ряда динамики за k лет.

Пример

Требуется рассчитать индексы сезонности объема продаж (млн руб.) за три последних года при следующих исходных данных.

Объем продаж	Месяц
	1	2	3	4	5	6	7	8	9	10	11	12
2008	7,1	7,7	8,5	9,7	10,9	11,4	10,1	9,5	8,4	8,4	9,7	11,5
2009	7,9	8,9	9,3	10,8	12,1	11,5	10,5	10,0	9,2	9,5	10,3	10,9
2010	9,7	9,9	11,4	12,9	14,9	12,1	11,0	9,8	7,9	8,2	9,9	12,0

Расчет индексов сезонности приведен в таблице.

1	7,1	7,9	9,7	24,7	8,2	0,90	0,81
2	7,7	8,9	9,9	26,5	8,8	0,91	0,87
3	8,5	9,3	11,4	29,2	9,7	1,05	0,96
4	9,7	10,8	12,9	33,4	11,1	1,19	1,10
5	10,9	12,1	14,9	37,9	12,6	1,38	1,25
6	11,4	11,5	12,1	35,0	11,7	1,12	1,15
7	10,1	10,5	11,0	31,6	10,53	1,02	1,04
8	9,5	10,0	9,8	29,3	9,8	0,91	0,96
9	8,4	9,2	7,9	25,5	8,5	0,73	0,84
10	8,4	9,5	8,2	26,1	8,7	0,76	0,86
11	9,7	10,3	9,9	29,9	10,0	0,91	0,98
12	11,5	10,9	12,0	34,4	11,5	1,11	1,13
Ук	9,4	10,1	10,8	30,3	10,1	–	–

В примере индексы сезонности, рассчитанные за три года, указывают на те же периоды пика и "ямы", что и индексы сезонности за 2010 г., но являются более уточненными. Такой подход к анализу сезонных колебаний приводит к снижению ошибок при расчете прогнозных значений показателей деятельности предприятия.