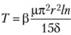Расход жидкости
Найдем расход жидкости, протекающей через данное сечение ламинарного потока. Выделим в потоке элементарное кольцо, ограниченное радиусами r и r + dr (рис. 6.9).
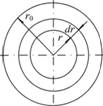
Рис. 6.9. Схема к выводу формулы для расхода жидкости
Элементарный расход составит
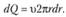
Полный расход будет
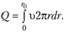(6.6)
Подставляя выражение (6.5) в формулу (6.6), получаем
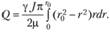
Вычисляя интеграл, будем иметь
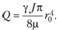(6.7)
Найдем среднюю по сечению скорость:
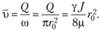(6.8)
Отношение средней скорости к максимальной будет
откуда
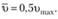
Выведем формулы для гидравлического уклона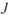 
.
Из уравнения для расхода (6.7), учитывая, что 
, получаем
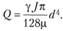
Отсюда
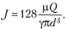(6.9)
Так как
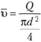и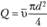 
,
то
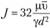(6.10)
Формулы (6.9) и (6.10) называются формулами Гагена – Пуазейля.
Из формулы (6.9) очевидно, что при одном и том же расходе гидравлический уклон обратно пропорционален диаметру в 4-й степени. Из формулы (6.10) следует, что гидравлический уклон прямо пропорционален средней скорости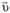
Коэффициент линейных потерь при ламинарном движении жидкости
Зная закон распределения скорости в поперечном сечении, можно вывести теоретические формулы для определения расхода жидкости, потери напора на трение, а также коэффициента линейных потерь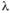
при ламинарном режиме течения.
Средняя по сечению скорость согласно формуле (6.8) равна
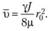
Учитывая, что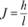 
и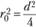 
, получаем
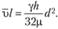
Отсюда
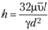, или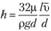 
После некоторых преобразований найдем
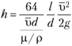
Отсюда получим
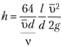
Сравнивая с формулой Дарси – Вейсбаха
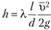
находим
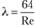
Последнее соотношение представляет формулу Пуазейля для определения коэффициента трения
(коэффициента линейных потерь).
Логарифмируя формулу Пуазейля, получаем
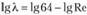
Из последнего соотношения следует, что зависимость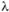
от Re будет выражаться в логарифмических координатах прямой линией с углом наклона к оси абсцисс, равным 45° (рис. 6.10).
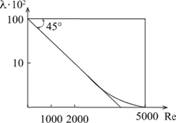
Рис. 6.10. График зависимости коэффициента гидравлического сопротивления от числа Рейнольдса
Многочисленные эксперименты полностью подтверждают правильность полученных теоретических выводов для ламинарного изотермического потока. Тем самым подтверждается и правильность закона Ньютона для внутреннего трения, положенного в основу этих выводов. При Re ≥ 2320, т.е. при турбулентном режиме, формула Пуазейля неприменима.
Основы гидродинамической теории смазки
Создателем гидродинамической теории смазки является профессор Н. П. Петров. До него считали, что в подшипниках скольжения происходит трение одного тела (вала) о другое (вкладыш).
Н. П. Петров показал, что при вращении вал увлекает за собой смазочную жидкость, направляя ее в зазор между валом и вкладышем в нижней части (рис. 6.11, а). От этого давление в зазоре между валом и вкладышем возрастает. Образуется своего рода масляный клин, вытесняющий вал вверх и влево (рис. 6.11, б). При увеличении числа оборотов п вал "всплывает". Таким образом, трения вала о вкладыш не происходит – сухое трение заменяется жидкостным. При увеличении числа оборотов вал стремится встать в центре отверстия во вкладыше (центр вала О1 совпадает с центром подшипника О – рис. 6.11, в).
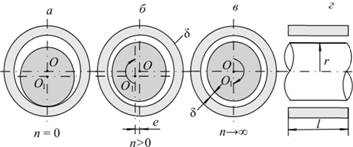
Рис. 6.11. Схема к выводу формулы Петрова
Вывод формулы Петрова для силы трения основывается на следующем. При одинаковой толщине слоя смазки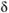
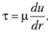
где и – окружная скорость.
При радиусе вата r и длине вкладыша l (рис. 6.11, г) полная поверхность, по которой происходит трение:
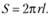
Тогда сила трения будет
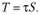
Так как
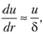
то
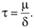
Отсюда
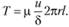
Учитывая, что
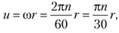
где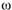
– угловая скорость; п – число оборотов вала, получаем
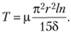
Так как слой смазки неодинаков по толщине, то всегда имеет место эксцентриситет е, учитываемый поправочным коэффициентом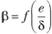 
Окончательно формула Петрова принимает вид
