фазы деформаций грунта под фундаментом

Закономерности распределения напряжений в грунте

в рамках общей темы

«Напряженное состояние грунтов в допредельном и предельном состояниях»

 

 

Решение задачи определения напряжений в грунте необходимо для установления условий прочности и устойчивости грунтов и определения их деформаций (например, осадок). При решении вопроса о распределении напряжений в грунтах в Механике грунтов применяют теорию линейно-деформируемых тел. То есть для определения напряжений могут быть применены уравнения и зависимости теории упругости, базирующиеся на линейной зависимости между напряжениями и деформациями (закон Гука). Однако при применении закона Гука для грунтов необходимо условиться об ограничениях, поскольку в грунтах возникают не только упругие, но значительные остаточные деформации.

 

общая зависимость между деформациями и напряжениями. Принцип линейной деформируемости

В основу теории распределения напряжений в грунтах кладётся зависимость между относительными деформациями и нормальными напряжениями .

В общем случае (согласно опытам) зависимость между деформациями и напряжениями для грунтов будет нелинейной:

 

 

 

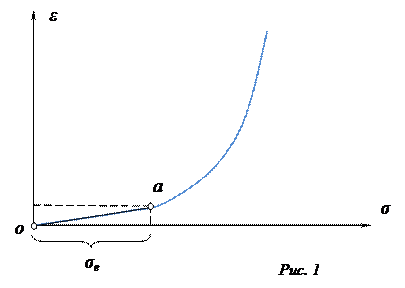
Однако в определенном интервале напряжений (при не очень больших изменениях внешних давлений – порядка 1÷3 кг/см2) с достаточной для практических целей точностью зависимость между деформациями и нормальными напряжениями может приниматься линейной (спрямлённый участок оа на кривой, рис. 1).

Сформулируем принцип линейной деформируемости для грунтов: при небольших изменениях давлений грунты можно рассматривать как линейно-деформируемые тела, то есть зависимость между общими деформациями и напряжениями для грунтов может быть принята линейной: = Е · .

 

напряжение, передаваемое грунту по подошве фундамента

Это напряжение не остается по глубине постоянным, а в некоторой области грунтовой толщи рассеивается. Для решения задач о распределении напряжений применяют уравнения теории упругости, рассматривая грунты как тела однородные, изотропные и линейно-деформируемые, подчиняющиеся закону Гука. Для оснований гражданских и промышленных зданий назначают такую величину допустимых напряжений, при которой в грунте не возникают пластические (остаточные) деформации.

Рассмотрим случай плоской задачи: фундаменты передают на грунт сплошную, распределенную полосовую нагрузку:

 
 

 

 


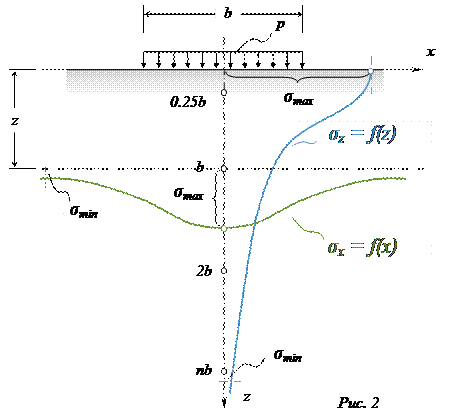Изменение напряжений по различным вертикальным (z) и горизонтальным (x) сечениям характеризуется эпюрами z и x (рис. 2). Как видно из рисунка, напряжения в грунтовой толще изменяются, как непрерывные функции от max до min как по вертикальному, так и по горизонтальному направлению.

В напряженной зоне грунта имеются точки с одинаковыми напряжениями, через которые можно провести линии (т.н. кривые равных напряжений). Например, линии, проходящие через точки с одинаковым вертикальным напряжением z, называются изобарами. В сжимаемой толще можно провести какое угодно число изобар (в зависимости от того, какие по величине напряжения соединяются линиями). Например, если к поверхности грунта приложена распределенная полосовая нагрузка интенсивностью p, то семейство изобар будет выглядеть следующим образом:

 
 

 

 


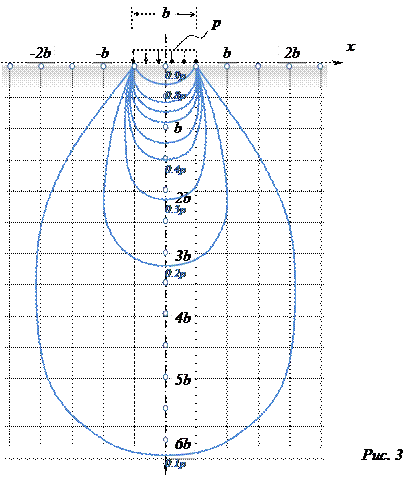Семейство изобар принято называть «луковицей напряжений». Построение «луковиц напряжений» полезно при оценке напряженного состояния в основаниях сооружений: подобное изображение наглядно иллюстрирует изменение напряжений в грунте под нагрузкой.

Фазы деформаций грунта под фундаментом

2
Закономерность нарастания осадок с постепенным увеличением статической нагрузки характеризуется графиком:

 
 

 

 


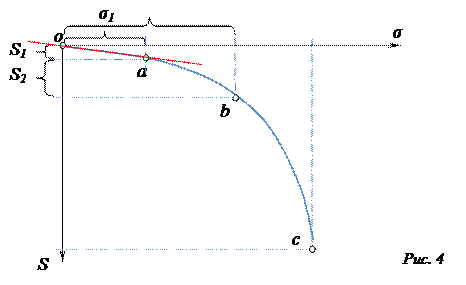Этот график имеет три характерных участка (oa, ab и bc на графике, рис. 4).

Начальный участок оа имеет пологое очертание и согласно принципу линейной деформируемости может быть заменён прямой. Деформация на участке прямой называется фазой уплотнения (рис. 5).

В фазе уплотнения происходит более плотная укладка частиц грунта за счёт уменьшения объёма пор. Ни в одной точке основания касательные напряжения по своей величине не превосходят сил внутреннего сопротивления грунта сдвигу, то есть повсюду существует состояние устойчивого равновесия грунта ( < пр).

Второй участок ab графика характерен значительной кривизной, где линейная зависимость – S нарушается. Здесь темп нарастания деформаций значительно опережает темп нарастания нагрузок. Обусловлено это тем, что как только нагрузка преодолеет значение 1 (рис. 4), в некоторых зонах «1» (рис. 6) возникнут напряжения, характеризуемые состоянием предельного равновесия ( = пр), возникнут пластические, остаточные деформации. По мере дальнейшего возрастания нагрузки области пластических деформаций расширяются, образуя зоны «2». Когда нагрузка достигает некоторого значения 2 (рис. 4), пластические деформации распространяются на всю область основания (зоны «3»). Деформация на участке ab называется фазой сдвигов (рис. 6).

 

 


Конечный участок bc соответствует моменту нарушения равновесия грунта ( > пр) и выпирания его из-под фундамента. Деформация на участке bc называется фазой выпирания (рис. 7).

 

       
 
 
   
Рис. 7. Фаза выпирания

 


Таким образом, при возрастании нагрузки на грунт необходимо различать две характерные её величины, при достижении которых резко меняется поведение грунта:

- первую, соответствующую началу перехода фазы уплотнения в фазу сдвигов – то есть фазу зарождения и развития зон предельного напряженного состояния;

- и вторую, когда исчерпывается несущая способность грунтового основания и наблюдается полное развитие зон предельного равновесия, при котором даже весьма незначительное увеличение нагрузки приводит грунт к потере прочности и устойчивости (к разрушению).

Список литературы, использованной при подготовке лекции:

 

1. Бартоломей А.А. Механика грунтов: Учеб. издание/ АСВ, Москва, 2004;

2. Малышев М.В., Болдырев Г.Г. Механика грунтов. Основания и фундаменты (в вопросах и ответах) / Учебное пособие. – М.: Издательство Ассоциации строительных вузов, 2004;

3. Тер-Мартиросян З.Г. Механика грунтов/ Учебное пособие. – М.: Издательство Ассоциации строительных вузов, 2005;

4. Цытович Н.А. Механика грунтов (краткий курс): Учебник для строит. вузов. – М.: Высш. шк., 1983.

5. Проектирование фундаментов зданий и подземных сооружений: Учеб. пособие/ Под ред. Б.И. Далматова; 2-е изд. – М.: Изд-во АСВ; СПб.: СПбГАСУ, 2001.

 

Список литературы, рекомендуемой студентам по данной теме:

 

1. Далматов Б.И. Механика грунтов, основания и фундаменты. – М.: Стройиздат, 1988;

2. Цытович Н.А. Механика грунтов (краткий курс): Учебник для строит. вузов. – М.: Высш. шк., 1983;

3. Бартоломей А.А. Механика грунтов: Учеб. издание/ АСВ, Москва, 2004;

4. К.З. Игнатенко, Т.Н. Пронкина. Механика грунтов. Методические указания к изучению дисциплины. Владивосток, ДВГТУ, 1997;

5. К.З. Игнатенко, Т.Н. Пронкина. Механика грунтов. Методические указания к выполнению лабораторных работ. Владивосток, ДВГТУ, 1998.