Воронеж 2008
В.М. Пачевский А.Н. Осинцев М.Н. Краснова
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ
И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ: ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО КОМПЛЕКСУ ДИСЦИПЛИН
Учебное пособие
Воронеж 2008
ГОУВПО «Воронежский государственный
технический университет»
В.М. Пачевский А.Н. Осинцев М.Н. Краснова
МЕТРОЛОГИЯ, СТАНДАРТИЗАЦИЯ
И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ: ЛАБОРАТОРНЫЙ ПРАКТИКУМ
ПО КОМПЛЕКСУ ДИСЦИПЛИН
Издание второе, переработанное и дополненное
Утверждено Редакционно-издательским советом
университета в качестве учебного пособия
Воронеж 2008
| |
УДК 621.02.01.2
Пачевский В.М. Метрология, стандартизация и технические измерения: лабораторный практикум по комплексу дисциплин: учеб. пособие / В.М. Пачевский, А.Н. Осинцев, М.Н. Краснова. 2-е изд., перераб. и доп. Воронеж: ГОУВПО «Воронежский государственный технический университет», 2008. 180 с.
Лабораторный практикум составлен в соответствии с программой курсов «Метрология, стандартизация и сертификация» (специальности 151001 «Технология машиностроения», 151002 «Металлообрабатывающие станки и комплексы», 150201 «Машины и технология обработки металлов давлением»), «Нормирование точности» (специальности 151002 «Металлообрабатывающие станки и комплексы») и «Взаимозаменяемость» (специальность 200503 «Стандартизация и сертификация») и содержит краткое изложение учебного материала, задания на лабораторные работы, объяснения по их выполнению.
Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлениям 151000 «Конструкторско-технологическое обеспечение автоматизированных машиностроительных производств», 150200 «Машиностроительные технологии и оборудование» и 200500 «Метрология, стандартизация и сертификация».
Предназначено для студентов очной и очно-заочной форм обучения.
Учебное пособие подготовлено в электронном виде в текстовом редакторе MS Word XP и содержится в файле Метр, станд. и техн. измер.: ЛП.doc.
Табл. 19. Ил. 76. Библиогр.: 5 назв.
Научный редактор д-р техн. наук, проф. М.И. Чижов
Рецензенты: кафедра начертательной геометрии и графики
Воронежского государственного
архитектурно-строительного университета
(зав. кафедрой д-р техн. наук, проф. Ю.А. Цеханов);
д-р техн. наук, проф. Ю.С. Ткаченко
© Пачевский В.М., Осинцев А.Н.,
Краснова М.Н., 2008
© Оформление. ГОУВПО
 «Воронежский государственный
«Воронежский государственный
технический университет», 2008
ВВЕДЕНИЕ
Современное машиностроение характеризуется широким внедрением современных, надежных и эффективных машин высокого качества. Непрерывно совершенствуются конструкции машин и других изделий, технология и средства их производства и контроля. Широко используются такие методы повышения технологичности изделий, как унификация и стандартизация изделий, их агрегатов и деталей; шире используются методы комплексной, и опережающей стандартизации; внедряются системы управления качеством продукции, система технологической подготовки производства. Увеличилась доля изделий высшей категории качества в общем объеме их производства.
Большое значение для развития машиностроения имеет организация производства машин и других изделий на основе взаимозаменяемости, создание и применение надежных средств технических измерений и контроля.
Комплекс дисциплин «Метрология, стандартизация и технические измерения», дает студенту знания, которые входят в основу обязательных знаний абсолютно для всех специалистов, работающих в любой отрасли машиностроения. Эти обязательные знания должны быть усвоены будущими специалистами. Этими знаниями специалист будет пользоваться все время, пока он будет работать в области машиностроения.
Эти знания, т.е. как нормируется точность в машиностроении и что это такое, какими параметрами нормируется точность, какими знаками и как эти требования должны обозначаться на чертежах, как и каким инструментарием производятся технические измерения, студент должен знать и владеть в совершенстве.
Важным элементом учебного процесса является лабораторный практикум. Выполнение лабораторных работ по дисциплине не только позволяет студентам закрепить теоретические знания, но и самостоятельно их применять на практике, хотя бы в рамках учебной задачи. Такой подход к лабораторным работам обязывает индивидуализировать задания, вносить в них элементы неожиданного, требующего творческого решения. При выполнении лабораторной работы студенты овладевают методами организации, подготовки и проведения эксперимента, анализом его результатов. В каждой лабораторной работе должна быть поставлена цель, только достижение ее служит основанием для окончания данной работы и ее защиты.
Методика проведения лабораторных занятий может существенно различаться для разных дисциплин, но форма их проведения должна быть активной. Студент должен на занятиях интенсивно работать. Очень важно, чтобы студенты имели четкое представление о том, какое отношение предлагаемые им задачи имеют или будут иметь к их будущей профессии.
В данном учебном пособии представлено 8 лабораторных работ, что превышает требования учебного курса. Выбор той или иной лабораторной работы диктуется количеством часов учебного плана, возможностями кафедры, ведущей данную дисциплину, требованиями производственных предприятий данного региона.
1. ОБЩИЕ ПОЛОЖЕНИЯ И УКАЗАНИЯ
К САМОСТОЯТЕЛЬНОЙ РАБОТЕ СТУДЕНТОВ
Учебное пособие разработано для проведения восьми лабораторных работ, связанных с изучением технических измерений и особенностями их практического применения.
Цель работ: закрепление теоретических знаний и приобретение практических навыков в подборе оптимальных методов измерения и измерительных средств для заданных поверхностей и проведение измерений в реальных условиях.
Время выполнения одной работы - 4 часа.
Не позднее, чем за две недели до проведения лабораторной работы студент должен знать номер той работы, которую он должен выполнять на следующем занятии. За это время студент знакомится с описанием лабораторной работы, изучает теоретические вопросы, продумывает возможные варианты выполнения работы.
Отчет по лабораторным работам оформляется в отдельной тетради. Он проводится в виде зашиты. Студент отчитывается в присутствии всей подгруппы. Каждый присутствующий может задавать вопросы и высказывать свое мнение по поводу выполненной работы.
В описании каждой лабораторной работе представлена информация по особенностям отчета.
2. МЕТРОЛОГИЯ И ТЕХНИЧЕСКИЕ ИЗМЕРЕНИЯ
2.1. Теоретическая часть
2.1.1. Основные понятия
Основными единицами физических величин в СИ являются: длины — метр (м), массы — килограмм (кг), времени — секунда (с), силы электрического тока — ампер (А), термодинамической температуры — кельвин (К), силы света — кандела (кд), количества вещества — моль (моль). Дополнительные единицы СИ: радиан (рад) и стерадиан (ср) — для измерения плоского и телесного углов соответственно.
Производные единицы СИ получены из основных с помощью уравнений связи между физическими величинами. Так, единицей силы является ньютон: 1Н = 1 кг∙м∙с-2, единицей давления — паскаль: 1 Па = 1 кг∙м–1 ∙с-2 и т. д. В СИ для обозначения десятичных кратных (умноженных на 10 в положительной степени) и дольных (умноженных на 10 в отрицательной степени) приняты следующие приставки: экса (Э) - 1018, пета (П) - 1015, тера (Т) - 1012, гига (Г) - 109, мега (М) - 106, кило (к) - 103, гекто (г) - 102, дека (да) - 101, деци (д) - 10 -1, санти (с) - 10 -2, милли (м) - 10 -3, микро (мк) - 10-6, нано (н) - 10-9, пико (п) - 10-12, фемто (ф) - 10-15, атто (а) - 10-18. Так, в соответствии с СИ тысячная доля миллиметра (микрометр) 0,001 мм = 1 мкм.
Средства измерений. Технические средства, используемые при измерениях и имеющие нормированные метрологические свойства, называют средствами измерения.
Эталоны — средства измерений, официально утвержденные и обеспечивающие воспроизведение и (или) хранение единицы физической величины с целью передачи ее размера нижестоящим по поверочной схеме средствам измерений.
Меры — средства измерений, предназначенные для воспроизведения заданного размера физической величины. В технике часто используют наборы мер, например, гирь, плоскопараллельных концевых мер длины (плиток), конденсаторов и т. п.
Образцовые средства измерений — меры, измерительные приборы или преобразователи, утвержденные в качестве образцовых для поверки по ним других средств измерений. Рабочие средства применяют для измерений, не связанных с передачей размера единиц.
Порядок передачи размера единиц физической величины от эталона или исходного образцового средства к средствам более низких разрядов (вплоть до рабочих) устанавливают в соответствии с поверочной схемой. Так, по одной из поверочных схем передача единицы длины путем последовательного лабораторного сличения и поверок производится от рабочего эталона к образцовым мерам высшего разряда, от них образцовым мерам низших разрядов, а от последних к рабочим средствам измерения (оптиметрам, измерительным машинам, контрольным автоматам и т. п.).
Методы измерений. При измерениях используют разнообразные методы (ГОСТ 16263—70), представляющие собой совокупность приемов использования различных физических принципов и средств. При прямых измерениях значения физической величины находят из опытных данных, при косвенных — на основании известной зависимости от величин, подвергаемых прямым измерениям. Так, диаметр детали можно непосредственно измерить как расстояние между диаметрально противоположными точками (прямое измерение) либо определить из зависимости, связывающей этот диаметр, длину дуги и стягивающую ее хорду, измерив непосредственно последние величины (косвенное измерение).
Абсолютные измерения основаны на прямых измерениях основных величин и использовании значений физических констант (например, измерение длины штангенциркулем). При относительных измерениях величину сравнивают c одноименной, играющей роль единицы или принятой за исходную. Примером относительного измерения является измерение диаметра вращающейся детали по числу оборотов соприкасающегося с ней аттестованного ролика.
При методе непосредственной оценки значение физической величины определяют непосредственно по отсчетному устройству прибора прямого действия (например, измерение давления пружинным манометром), при методе сравнения с мерой измеряемую величину сравнивают с мерой. Например, с помощью гирь уравновешивают на рычажных весах измеряемую массу детали. Разновидностью метода сравнения с мерой является метод противопоставления, при котором измеряемая величина и величина, воспроизводимая мерой, одновременно воздействуют на прибор сравнения, позволяющий установить соотношение между этими величинами (например, измерение сопротивления по мостовой схеме с включением в диагональ моста показывающего прибора).
2.1.2. Методы планирования измерений
При планировании измерений выбирают оптимальное число точек или кривых измерения, поскольку слишком большое число измерений приводит к удорожанию и усложнению эксперимента и может не дать новых сведений, а заниженное число измерений не позволяет надежно оценить выбранную точность метода или средства измерений. Используя математическое доказательство подобия, правомерность сравнения и моделирование процессов измерения и число предварительных наблюдений, заведомо меньшее, чем требуемое, можем вычислить необходимое число наблюдений.
Определение наименьшего числа измерений для достижения заданной точности измерения проводится в следующем порядке:
1. Выполнить четыре измерения заданного преподавателем размера детали (например, наружного диаметра вала).
2. Исключить из результатов измерений известные систематические погрешности (например, отклонения от нуля у средства измерения).
3. Вычислить среднее арифметическое исправленных результатов измерений
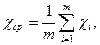 (2.1)
(2.1)
где χср - среднее арифметическое,
χi - результаты измерений,
m - количество измерений.
4. Вычислить m абсолютных отклонений от среднего
 (2.2)
(2.2)
5. Вычислить величину среднеквадратического отклонения результатов измерений по формуле:
 (2.3)
(2.3)
6. Определить наименьшее число наблюдений n для достижения требуемой точности измерения по формуле:
 (2.4)
(2.4)
где n - оптимальное число наблюдений;
m - предварительное число наблюдений;
Sm - среднеквадратическое отклонение;
tm-1 - табличный коэффициент Стьюдента (tm-1 = 4,3 для доверительной вероятности P = 0,95 и числа наблюдений
m = 4);- погрешность измерения.
При дифференциальном методе измеряемую величину сравнивают с известной величиной, воспроизводимой мерой. Этим методом, например, определяют отклонение контролируемого диаметра детали на оптиметре после его настройки на ноль по блоку концевых мер длины. Нулевой метод — также разновидность метода сравнения с мерой, при котором результирующий эффект воздействия величин на прибор сравнения доводят до нуля. Подобным методом измеряют электрическое сопротивление по схеме моста с полным его уравновешиванием. При методе совпадений разность между измеряемой величиной и величиной, воспроизводимой мерой, определяют, используя совпадения отметок шкал или периодических сигналов (например, при измерении штангенциркулем используют совпадение отметок основной и нониусной шкал). Поэлементный метод характеризуется измерением каждого параметра изделия в отдельности (например, эксцентриситета, овальности, огранки цилиндрического вала). Комплексный метод характеризуется измерением суммарного показателя качества, на который оказывают влияния отдельные его составляющие (например, измерение радиального биения цилиндрической детали, на которое влияют эксцентриситет, овальность и др.; контроль положения профиля по предельным контурам и т. п.).
2.1.3. Универсальные средства измерений
Основные параметры средств измерений. Длина деления шкалы (рис. 2.1) – расстояние между осями (центрами) двух соседних отметок шкал, измеренное вдоль воображаемой линии, проходящей через середины самых коротких отметок шкалы. Цена деления шкалы – разность значений величины, соответствующих двум соседним отметкам шкал (1 мкм для оптиметра, длиномера и т.п.).
Градуированная характеристика — зависимость между значениями величин, на выходе и входе средства измерений. Градуировочную характеристику снимают для уточнения результатов измерений.
Диапазон показаний — область значений шкалы, ограниченная конечным и начальным значениями шкалы, т. е. наибольшим и наименьшим значениями измеряемой величины. Например, для оптиметра типа ИКВ-3 диапазон показаний составляет ± 0,1 мм.
Диапазон измерений — область значений измеряемой величины с нормированными допускаемыми погрешностями средства измерений.

Рис. 2.1. Схема, поясняющая основные параметры
средств измерений
Отсчет показаний измерительного средства выполняют в соответствии с уравнением:
 (2.5)
(2.5)
где А — значение отсчета;
М — размер меры, по которому отсчетное устройство установлено на ноль;
n — число целых делений, отсчитываемое по шкалам отсчетного устройства;
i — цена деления шкалы;
k — номер шкалы,
m — доля деления шкалы с наименьшей ценой деления, оцененная визуально.
Влияющая физическая величина — физическая величина, не измеряемая данным средством, но оказывающая влияние на результаты измеряемой величины (например, температура, оказывающая влияние на результат измерения линейного размера).
Нормальные (рабочие) условия применения средств измерений — условия их применения, при которых влияющие величины имеют нормальные значения или находятся в пределах нормальной (рабочей) области значений.
Чувствительность измерительного прибора - отношение изменения сигнала на выходе измерительного приборам вызывающему его изменению измеряемой величины. Так, если при измерении диаметра вала с номинальным размером χ = 100 мм изменение измеряемой величины Δχ = 0,01 мм вызвало перемещение стрелки показывающего устройства на Δl = 10 мм, абсолютная чувствительность прибора составляет
S = Δl / Δχ; = 10/0,01 = 1000, относительная чувствительность
So = Δl (Δχ / χ) = 10 (0,01/100) = 10 000. (2.6)
Для шкальных измерительных приборов абсолютная чувствительность численно равна передаточному отношению. С изменением цены деления шкалы чувствительность прибора остается неизменной. На разных участках шкалы часто чувствительность может быть различной. Стабильность средства измерений — свойство, выражающее неизменность во времени его метрологических характеристик (показаний).
Измерительные приборы бывают контактные (существует механический контакт с поверхностью контролируемого изделия) и бесконтактные (непосредственного соприкосновения измерительного наконечника с поверхностью контролируемого изделия нет). К последним, например, относятся оптические, радиоизотопные, индуктивные. Важной характеристикой контактных приборов является измерительное усилие, создаваемое в месте контакта измерительного наконечника с поверхностью контролируемого изделия и направленное по линии измерения.
В соответствии с техническим регламентом геометрический объект контроля содержит одну или несколько контрольных точек. Введем дополнительные термины, необходимые для оценки результатов контроля (измерений). Зона контроля (измерения) — область взаимодействия средства контроля (измерения) с объектом контроля (измерения). Контролируемая (измеряемая) поверхность — поверхность объекта контроля (измерения), на которой расположена одна или несколько контрольных точек. Линия контроля (измерения) — прямая, проходящая через контролируемый (измеряемый) размер. Плоскость контроля (измерения) — плоскость, проходящая через линию контроля (измерения) и выбранную линию расположения контрольных точек.
В технических регламентах выделены следующие общие для средств измерений структурные элементы: преобразовательный и чувствительный элементы, измерительная цепь, измерительный механизм, отсчетное устройство со шкалой и указателем и регистрирующее устройство. Кроме того, контактные измерительные приборы обычно снабжены одним или несколькими наконечниками. Измерительный наконечник — элемент в измерительной цепи, находящийся в контакте с объектом контроля (измерения) в контрольной точке под непосредственным воздействием измеряемой величины. Базовый наконечник — элемент измерительной цепи, расположенный в плоскости измерения и служащий для определения длины линии измерения. Опорный наконечник — элемент, определяющий положение линии измерения в плоскости измерения. Координирующий наконечник - элемент, служащий для определения положения плоскости измерения на объекте контроля (измерения).
2.1.4. Критерии оценки погрешностей измерений
Погрешности измерения. Под погрешностью измерения подразумевают отклонение результата измерения от истинного значения измеряемой величины. Точность измерений — качество измерения, отражающее близость их результатов к истинному значению измеряемой величины. Количественно точность измерения может быть выражена обратной величиной модуля относительной погрешности. Абсолютная погрешность измерения — разность между значением величины, полученным при измерении, и ее истинным значением, выражаемая в единицах измеряемой величины. Относительная погрешность измерения — отношение абсолютной погрешности, измерения к истинному значению измеряемой величины. Систематическая погрешность измерения — составляющая погрешности измерения, остающаяся постоянной или изменяющаяся по определенному закону при повторных измерениях одной и той же величины; случайная погрешность — составляющая погрешности измерения, изменяющаяся при этих условиях случайным образом. Следует выделять также грубую погрешность измерения, существенно превышающую ожидаемую погрешность.
В зависимости от последовательности причины возник-новения различают следующие виды погрешностей. Инструментальная погрешность — составляющая погрешности измерения, зависящая от погрешностей применяемых средств (качества их изготовления). Погрешность метода измерения — составляющая погрешности измерения, вызванная несовершенством метода измерений. Погрешность настройки — составляющая погрешности измерения, возникающая из-за несовершенства осуществления процесса настройки. Погрешность отсчитывания — составляющая погрешности измерения, вызванная недостаточно точным отсчитыванием показаний средств измерений (например, погрешность параллакса). Погрешность поверки — погрешность измерений при поверке средств измерений. Таким образом, в зависимости от способа выявления следует различать поэлементные (составляющие) и суммарные погрешности измерения.
Результат наблюдения — значение величины, полученное при отдельном наблюдении; результат измерения — значение величины, найденное путем ее измерения, т. е. после обработки результатов наблюдения.
Поправка — значение величины, одноименной с измеряемой, прибавляемое к полученному при измерении значению величины с целью исключения систематической погрешности. Сходимость — качество измерений, отражающих близость результатов измерений, выполняемых в одинаковых условиях, воспроизводимость — то же, в различных условиях (в разное время, в различных местах, различными методами и средствами). Точность отражает близость к нулю случайных и систематических погрешностей средства измерения, правильность — систематических, сходимость — случайных. Для средств измерения различают статическую погрешность как отклонение постоянного значения измеряемой величины на выходе средства измерения от истинного ее значения в установившемся состоянии и динамическую погрешность как разность между погрешностью средства измерения в динамическом режиме (в неустановившемся состоянии) и его статической погрешностью, соответствующей значению величины в данный момент времени.
Погрешность средства измерения, возникающая при использовании его в нормальных условиях, когда влияющие величины находятся в пределах нормальной области значений, называют основной. Если значение влияющей величины выходит за пределы нормальной области значений, появляется дополнительная погрешность.
Обобщенной характеристикой средства измерений, определяемой пределами основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерения, является класс точности средства измерений. Класс точности характеризует свойства средства измерения, но не является показателем точности выполненных измерений, поскольку при определении погрешности измерения необходимо учитывать погрешности метода, настройки и др.
2.2. Лабораторные работы
2.2.1. Лабораторная работа № 1