МЕТОДОМ КРУТИЛЬНЫХ КОЛЕБАНИЙ
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛА
Методические указания к лабораторной работе №14 по физике
(Раздел «Механика»)
Ростов-на-Дону
Составители: А.А.Андрющенко, Н.Г.Последова
УДК 530.1
ОПРЕДЕЛЕНИЕ МОМЕНТА ИНЕРЦИИ ТЕЛ МЕТОДОМ
КРУТИЛЬНЫХ КОЛЕБАНИЙ
Метод. указания. - Ростов н/Д:
Издательский центр ДГТУ, 2009. - 11 с.
Указания содержат описание рабочей установки и методики определения момента инерции тел методом крутильных колебаний.
Методические указания предназначены для студентов инженерных специальностей всех форм обучения в лабораторном практикуме по физике (раздел «Механика и молекулярная физика»).
Печатается по решению методической комиссии факультета «Нанотехнологии и композиционные материалы»
Научный редактор проф., д.т.н. В.С.Кунаков
© Издательский центр ДГТУ, 2009
I. Цель работы: определение момента инерции тела методом крутильных
колебаний.
II. Приборы и принадлежности: экспериментальная установка, секундомер, штангенциркуль, измерительная линейка.
III. Теоретическая часть.
При изучении вращательного, либо колебательного движений твердого тела используют понятие момента инерции. Моментом инерции твердого тела (либо системы тел) относительно некоторой оси называется физическая величина, равная сумме произведения масс материальных точек системы на квадрат их расстояний до оси вращения:
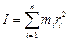 ,
,
где n – число материальных точек, составляющих тело, либо систему тел.
В случае непрерывного распределения масс момент инерции может быть определен интегралом: 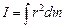 ,
,
где r – функция положения точки массой dm.
Момент инерции зависит от массы тела и формы распределения массы относительно оси вращения.
Гармоническим крутильным колебанием тела называется периодическое движение относительно оси, проходящей через центр тяжести этого тела, когда угол отклонения от положения равновесия изменяется по закону синуса или косинуса:
 , (1)
, (1)
где j – угловое смещение, j0 – максимальное угловое смещение,
 – циклическая частота, Т – период колебаний.
– циклическая частота, Т – период колебаний.
Угловое ускорение колебаний определяется как вторая производная от углового смещения по времени:
 (2)
(2)
С учетом (1) равенство (2) можно переписать в виде:
 (3)
(3)
Если твердое тело совершает крутильные колебания, то к нему может быть применен основной закон динамики вращательного движения:
 (4)
(4)
где M – вращающий момент (момент возвращающей силы) относитель-но оси ОО1 (Рис1), I – момент инерции тела относительно той же оси.
Знак « – » указывает на то, что возвращающий момент всегда направлен к положению равновесия. Закрученная нить создаёт противодействующий момент силы упругости Мупр., который при малых углах закручивания j по закону Гука пропорционален этому углу:
 (5)
(5)
где N – направляющий момент, зависящий только от материала нити, её длины и сечения и является величиной постоянной для данного лабораторного прибора.
Возвращающий момент M и момент силы упругости Мупр. равны между собой и приравнивая правые части уравнений (4) и (5), получим:
 (6)
(6)
При помещении на испытуемое тело (см. рис.1) двух одинаковых грузов цилиндрической формы массой m каждый, момент инерции системы, состоящей из испытуемого тела и грузов, будет равен:
 (7)
(7)
где I0 – момент инерции двух грузов относительно оси ОО1.
Согласно теореме Штейнера момент инерции двух цилиндров относительно оси ОО1 равен:
 (8)
(8)
где а – расстояние от оси вращения ОО1 до оси цилиндров,
r – радиус цилиндра.
Момент инерции испытуемого тела и двух цилиндров будет равен:
 (9)
(9)
В соответствии с равенством (6) для нагруженного тела также выполняется условие
 (10)
(10)
Приравнивая правые части уравнений (6) и (10), получаем:

откуда находим момент инерции испытуемого тела
 (11)
(11)
Учитывая, что  и
и  , получаем:
, получаем:
 (12)
(12)
где Т – период колебаний испытуемого тела без грузов,
Т1 – период колебаний испытуемого тела с грузами.
IV. Описание экспериментальной установки.
 |
На рис.1 показана принципиальная схема лабораторного прибора для определения момента инерции тела методом крутильных колебаний.
Исследуемое телоВ, выполненное в виде стержня прямоугольного сечении, подвешено на упругой металлической нити ОО1, жестко закрепленной в точках О и О1 .Точка О является центром масс стержня. При повороте стержня на небольшой угол j0 относительно оси ОО1, перпендикулярной к плоскости стержня и проходящей через его центр, он начинает совершать крутильные колебания в горизонтальной плоскости, период которых будет зависеть от момента инерции системы и направляющего момента.
V. Порядок выполнения работы.
1. Заставить исследуемое тело совершать крутильные колебания с малой амплитудой (10 ¸ 15 градусов). Секундомером измерить время t совершения n полных колебаний (n – задаётся преподавателем).
2. Определить период колебаний испытуемого тела без грузов
Т = t /n.
3. Установить два груза на одинаковом расстоянии аот оси ОО1 и
аналогично пункту 1 определить период колебаний испытуемого тела с грузами
Т1 = t 1/n.
4. Все измерения (пункты 1 – 2) провести несколько раз (число измерений задает преподаватель). Все значения занести в таблицу 1.
5. Штангенциркулем измерить радиус грузов, а линейкой – расстояние «а» между осями (см. рис.1). Массу грузов m (приведена в паспорте установки), радиус грузов и расстояние азанести в таблицу 3.
6. Произвести статистическую обработку результатов измерений
времени t и t1 (для примера см. таблицы 1 и 2).
7. По формуле (12) определить момент инерции испытуемого тела.
8. По формуле (6) определить направляющий момент

9. Вычислить относительные и абсолютные погрешности по формулам (13) – (14) и занести результаты в таблицу 3.
Абсолютная погрешность периода колебаний определяется следующим образом

 аналогично
аналогично 
 , (13)
, (13)
 . (14)
. (14)
Таблица 1
| №/№ п/п | ti | D ti | Dti2 | Sn | t(a,n) | D tсл | D tпр | D t | T | DT |
| с | c | с2 | С | - | с | c | c | c | c | |
| … | ||||||||||
| N | ||||||||||
| Среднее |
Таблица 2
| №/№ п/п | t1i | D t1i | Dt1i 2 | Sn | t(a,n) | D t 1cл | D tпр | D t1 | T1 | DT1 |
| с | c | с2 | с | - | с | c | c | c | с | |
| … | ||||||||||
| N | ||||||||||
| Среднее |
Таблица 3.
| m | a | r | I0 | N | |
| Среднее значение | … кг | … м | … м | … кг×м2 | … 
|
| Абсолютная погрешность | … кг | … м | … м | … кг×м2 | … 
|
| Относительная погрешность | … % | … % | … % | … % | … % |
| Доверительный интервал | … кг×м2 | … 
|
IV. Контрольные вопросы.
1. Запишите основной закон динамики вращательного движения.
2. Каков физический смысл момента инерции?
3. Чему равен момент инерции материальной точки и твердого тела?
4. Запишите моменты инерции тел простейшей формы относительно оси, проходящей через центр инерции.
5. Запишите наименование и размерность момента инерции.
6. Дайте формулировку теоремы Штейнера и поясните её рисунком.
7. Дайте определение гармонических крутильных колебаний, запишите его уравнение и поясните физический смысл входящих в него величин.
8. Исходя из уравнения гармонических колебаний, определите угловое ускорение. Как определяется направление углового ускорения?
9. Дайте определение периода, частоты, циклической частоты
колебаний и покажите, как они связаны между собой.
10. Дайте формулировку закона Гука и поясните смысл входящих в него параметров.
11. Укажите условия выполнения закона Гука.
Рекомендуемая литература
1. Савельев И.В. Курс общей физики (т.1). М.: Наука, СПб.: Лань, 2006.
2. Трофимова Т.И. Курс физики. М.: Высш. шк., 2004.
3. Справочное руководство по физике. Ч.1. Механика, молекулярная физика, электричество, магнетизм: Учеб.-метод. пособие.-Ростов н/Д: Издательский центр ДГТУ, 2008.
Техника безопасности
1. К работе с установкой допускаются лица, ознакомленные с её устройством и принципом действия.
2. Нельзя сильно натягивать нить во избежание ее обрыва.
Составители: А.А.Андрющенко, Н.Г.Последова