Множество действительных (вещественных) чисел, .

ПП 10. Функции. Непрерывность

ОСНОВНЫЕ ОПРЕДЕЛЕНИЯ И ФОРМУЛЫ

Числовые множества

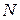– множество натуральных чисел ;

– множество целых чисел ;

– множество рациональных чисел вида ;

– множество иррациональных чисел .

множество действительных (вещественных) чисел, .

носится к установлению соответствия между элементами двух множеств.

Если задано правило , по которому каждому элементу из множества поставлен в соответствие единственный элемент из множества , то говорят, что на множестве задана функция , , . Множество называется областью определения функции (ООФ) и обозначается . Множество изменения функции называется областью значений функции (ОЗФ) и обозначается .

При нахождении области определения следует помнить, что:

; ; ;

; .

При аналитическом задании функция может быть определена:

1) явно - уравнением вида ;

2) неявно - уравнением вида ; Уравнение может определять не одну, а несколько функций вида . Так, уравнение определяет две функции: и .

3) параметрически – .

Функция с симметричной относительно нуля областью определения называется четной, если для любого выполняется равенство .

Из определения четной функции следует, что ее график симметричен относительно оси ординат. Например, функции , являются четными, их графики имеют вид:

Функция с областью определения называется нечетной, если для любого выполняется равенство .

График нечетной функции симметричен относительно начала координат. Например, функции и являются нечетными, их графики имеют вид:

Функция не является ни четной, ни нечетной, так как .

Функция называется периодической, если существует такое число , что для любого выполнены условия: 1) ;
2) .

Число называется периодомфункции.

Если – период, то тоже является периодом:

,

а также

, , .

Наименьший положительный период называется основнымпериодом данной периодической функции.

Основной период функций , равен , а функций , равен . Период функций и равен . Функция основногопериодане имеет, так как при любом , в том числе и при .

Функция называется ограниченной на множестве , если

.

Например, функция ограничена на всей числовой оси; ограничена на любом промежутке конечной длины, но не ограничена на всей области определения .

Функция называется ограниченной сверху (снизу) на множестве , если ; ( ).

Например, ограничена снизу на всей области определения .

Точная верхняя (нижняя) грань множества значений функции на называется точной верхней (нижней) гранью функции на и обозначается ( ).

Например, , .

Если число ( ) принадлежит множеству значений функции на , то оно называется наибольшим (наименьшим) значением на и обозначается ( ).

Например, , не существует.

Пусть определена на множестве и множество .

Если :

- возрастающая на ;

- неубывающая на ;

- убывающая на ;

- невозрастающая на .

Все четыре типа в совокупности называются монотонными на , а возрастающие и убывающие - строго монотонными на .

Обратная функция. Сложная функция

Функция , , обратима, если каждое свое значение она принимает один раз, то есть для каждого существует только одно значение такое, что .

Для нахождения обратной функции нужно:

1. выразить через ;

2. поменять местами и .

Множество значений обратной функции совпадает с областью определения функции , а область определения обратной функции совпадает с множеством значений функции .

Графики функций и симметричны относительно биссектрисы первого и третьего координатных углов, то есть прямой .

Если и - функции одного переменного, то функция , определенная соотношением на области , называется сложной функцией или суперпозицией (композицией) функций и и обозначается .

Основные элементарные функции

1. Степенные функции

1.1. .
1.2. , .
1.3. .
1.4. .

2. Трансцендентные функции

2.1. Показательная .	2.2. Логарифмическая .
3. Тригонометрические функции
3.1.	3.2.
3.3.	3.4. .

.

4. Обратные тригонометрические функции
4.1. . .	4.2. . .
4.3. , .	4.4. . .
, , .
5. Гиперболические функции
5.1. Гиперболический синус .	5.2. Гиперболический косинус .
5.3. Гиперболический тангенс .	5.4. Гиперболический котангенс .

, ,

, .

Непрерывность функции

Определение 1.

Пусть функция определена на множестве и пусть точка . Функция называется непрерывной в точке , если 1) , 2) , 3) .

Функция называется непрерывной в точке ,если по любому можно указать такое , что ,если .

Определение 2.

Функция называется непрерывной в точке , если функция определена в точке и при этом , то есть бесконечно малым приращениям аргумента соответствуют бесконечно малые приращения функции.

Определение 3.

Функция называется непрерывной в точке , если функция определена в точке , существуют односторонние пределы и при этом .

Функция называется непрерывной в точке слева, если функция определена в точке и существует односторонний предел и при этом .

Функция называется непрерывной в точке справа, если функция определена в точке и существует односторонний предел и при этом .

Функция, непрерывная в любой точке множества , называется непрерывной на множестве .

12
• Далее ⇒