Определение силовых и кинематических параметров привода
Числа оборотов валов и угловые скорости:
n1 = nдв = 950 об/мин w1 = 950π/30 = 99,5 рад/с
n2 = n1/u1 = 950/3,15 = 302 об/мин w2= 302π/30 = 31,6 рад/с
n3 = n2/u2 = 302/7,01 = 43 об/мин w3= 43π/30 = 4,50 рад/с
Фактическое значение скорости грузовой цепи
v = zpn3/6·104 = 9·100·43/6·104 = 0,645 м/с
Отклонение фактического значения от заданного
δ = (0,65 – 0,645)100/0,65 = 0,8 < 7%
Мощности передаваемые валами:
P1 = Pтрηмηпк = 3750·0,98·0,995 = 3656 Вт
P2 = P1ηзпηпк = 3656·0,96·0,995 =3493 Вт
P3 = P2ηопηпс = 3493·0,94·0,99 = 3250 Вт
Крутящие моменты:
Т1 = P1/w1 = 3656/99,5 = 36,7 Н·м
Т2 = 3493/31,6 =110,7 Н·м
Т3 = 3250/4,50 = 722,2 Н·м
 Результаты расчетов сводим в таблицу
Результаты расчетов сводим в таблицу
Таблица 2.1
Силовые и кинематические параметры привода
| Вал | Число оборотов об/мин | Угловая скорость рад/сек | Мощность кВт | Крутящий момент Н·м |
| Вал электродвигателя | 99,5 | 3,656 | 36,7 | |
| Ведомый редуктора | 31,6 | 3,493 | 110,7 | |
| Рабочий привода | 4,50 | 3,250 | 722,2 |
 3 Выбор материалов зубчатых передач и определение допускаемых напряжений
3 Выбор материалов зубчатых передач и определение допускаемых напряжений
Принимаем, согласно рекомендациям [1c.52], сталь 45:
шестерня: термообработка – улучшение – НВ235÷262 [1c.53],
колесо: термообработка – нормализация – НВ179÷207.
Средняя твердость зубьев:
НВ1ср = (235+262)/2 = 248; НВ2ср = (179+207)/2 = 193
Допускаемые контактные напряжения:
[σ]H = KHL[σ]H0,
где KHL – коэффициент долговечности
KHL = (NH0/N)1/6,
где NH0 = 1·107 [1c.55],
N = 573ωLh = 573·31,6·16,0·103 = 29·107.
Так как N > NH0, то КHL = 1.
[σ]H1 = 1,8HB+67 = 1,8·248+67 = 513 МПа.
[σ]H2 = 1,8HB+67 = 1,8·193+67 = 414 МПа.
[σ]H = 0,45([σ]H1 +[σ]H2) = 0,45(513+414) = 417 МПа.
Допускаемые напряжения изгиба:
[σ]F = KFL[σ]F0,
где KFL – коэффициент долговечности
Так как N > NF0 = 4·106, то КFL = 1.
[σ]F01 = 1,03HB1 = 1,03·248 = 255 МПа.
[σ]F02 = 1,03HB2 = 1,03·193 = 199 МПа.
[σ]F1 = 1·255 = 255 МПа; [σ]F2 = 1·199 = 199 МПа.
Таблица 3.1
Механические характеристики материалов зубчатой передачи
| Элемент передачи | Марка стали | Dпред | Термоо-бработка | НВср | σв | σ-1 | [σ]Н | [σ]F |
| Sпред | Н/мм2 | |||||||
| Шестерня | 125/80 | Улучш. | ||||||
| Колесо | - | Норм-ия |
 4 Расчет закрытой конической передачи
4 Расчет закрытой конической передачи
Внешний делительный диаметр колеса
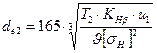 ,
,
где KHB = 1,1 – коэффициент, учитывающий распределение нагрузки по ширине венца для колес с круговыми зубьями
 = 1,85 – коэффициент вида конических колес
= 1,85 – коэффициент вида конических колес
de2 = 165×[(110,7×103×1,1×3,15)/(1,85·4172 )]1/3= 175 мм
Принимаем по ГОСТ 12289–766 de2 = 180 мм
Углы делительных конусов
сtgd1 = u1 = 3,15 ® d1 = 17,61°,
d2 = 90o – d1 = 90o – 17o36’ = 72,39o.
Внешнее конусное расстояние Re и длина зуба b
Re = de2/(2sinδ2) = 180/(2sin72,39°) = 94 мм,
b = bRRe
где bR = 0,285 – коэффициент ширины колеса
b = 0,28594 = 25 мм
Внешний окружной модуль
mte = 14T2KFβ /(  Fde2b[σ]F
Fde2b[σ]F
где  А = 1 – для колес с круговыми зубьями,
А = 1 – для колес с круговыми зубьями,
КFβ = 1,08 – для колес с круговыми зубьями
mte = 14·110,7·103·1,08/(1,0·180·25·199) = 1,87 мм.
Число зубьев колеса и шестерни
z2 = de2/mte = 180/1,87 = 96
z1 = z2/u1 = 96/3,15 = 31
Фактическое передаточное число конической передачи
u1 = z2/z1 = 96/31 = 3,10
Отклонение ∆ = (3,15 – 3,10)100/3,15 = 1,6% < 7%
 По таблице 4.6 [1c.68] находим коэффициент смещения для шестерни и колеса хn1 = 0,21; хn2 = -0,21
По таблице 4.6 [1c.68] находим коэффициент смещения для шестерни и колеса хn1 = 0,21; хn2 = -0,21
Диаметры шестерни и колеса
de1 = mtez1 = 1,87·31 = 57,97 мм
Диаметры вершин зубьев
dae1 = de1+ 1,64(1+xn1)mtecos δ1 =
= 57,97+1,64(1+0,21)1,87·cos17,61° = 61,51 мм
dae2 = de2 + 1,64(1 – xn2)mtecos δ2 =
= 180 + 1,64(1 + 0,21)1,87·cos72,39° =181,12 мм
Диаметры впадин зубьев
dfe1 = de1– 1,64(1,2–xn1)mtecos δ1 =
= 57,97– 1,64(1,2–0,21)1,87·cos17,61° = 55,08 мм
dfe2 = de2 – 1,64(1,2 + xn2)mtecos δ2 =
= 180 – 1,64(1,2 – 0,21)1,87·cos72,39° =179,08 мм
Средние делительные диаметры
d1 ≈ 0,857de1 = 0,857·57,97 = 49,68 мм
d2 ≈ 0,857de2 = 0,857·180 = 154,26 мм
Силы действующие в зацеплении:
окружная
Ft= 2T1/d1 = 236,7103/49,68 = 1478 Н
радиальная для шестерни, осевая для колеса
Fr1 = Fa2 = Ftγr = 1478·0,208 = 307 H
где γr – коэффициент радиальной силы
γr = (0,44cosδ1 – 0,7sinδ1) = 0,44cos17,61° – 0,7sin17,61° = 0,208
осевая для шестерни, радиальная для колеса
Fa1= Fr2 = Ftγa = 1478·0,80 =1182 H
где γа – коэффициент осевой силы
γа = (0,44sinδ1 + 0,7cosδ1) = 0,44sin17,61° + 0,7cos17,61° = 0,80
 Средняя окружная скорость.
Средняя окружная скорость.
V = ω2d2/2×103 = 31,6·154,26/2×103 = 2,4 м/с.
Принимаем 7 – ую степень точности.
Расчетное контактное напряжение

где КН – коэффициент нагрузки
KH = KHαKHβKHv =1,001,03·1,1 =1,133
KHα = 1,00 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]
KHβ = 1,1–коэффициент учитывающий неравномерность распределения нагрузки по ширине венца [1c.65]
KHv = 1,03 – динамический коэффициент [1c62]
σН = 470{1478×1,133[(3,102+1)]1/2/(1,85·25×180)}1/2 = 380 МПа
Недогрузка (417 – 380)100/417= 8,9 %
Допускаемая недогрузка 10%,
Проверяем напряжения изгиба зубьев шестерни и колеса
σF2 = YF2YβFtKFαKFβKFv/(  Fbmte)
Fbmte)
σF1 =σF2YF1/YF2
где YF – коэффициент формы зуба, зависящий от эквивалентного числа зубьев
zv= z/(cos·cos3β)
β = 35° - угол наклона зубьев
zv1 = 31/(cos17,61°·cos335°) = 59,2 → YF1 = 3,56
zv2 = 96/(cos72,39°·cos335°) = 577 → YF2 = 3,63
Yβ = 1 – коэффициент учитывающий наклон зуба
KFα = 1,0 – коэффициент учитывающий неравномерность распределения нагрузки между зубьями [1c.69]
 KFβ = 1,0 – для прирабатывающихся зубьев
KFβ = 1,0 – для прирабатывающихся зубьев
КFv = 1,07 – коэффициент динамичности [1c62]
σF2 = 3,63·1,0·1478·1,0·1,0·1,07/(1,0·25·1,87) = 123 МПа < [σ]F2
σF1 = 120·3,56/3,63 = 120 МПа < [σ]F1
Так как расчетные напряжения σH < [σH] и σF < [σ]F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.
 5 Расчет открытой цилиндрической передачи
5 Расчет открытой цилиндрической передачи
Выбор материалов передачи
Принимаем те же материалы, что и в закрытой передаче.
Межосевое расстояние
 ,
,
где Ка = 49,5 – для прямозубых передач [1c.58],
ψba = 0,20 – коэффициент ширины колеса,
КНβ = 1,0 – для прирабатывающихся колес.
аw = 49,5(7,01+1)[722,2·103·1,0/(4172·7,012·0,20)]1/3 = 298 мм
принимаем согласно ГОСТ 2185-66 [2 c.52] аw = 280 мм.
Модуль зацепления
m > 2KmT2/(d2b2[σ]F),
где Km = 6,8 – для прямозубых колес,
d4 – делительный диаметр колеса,
d4 = 2awu/(u+1) = 2·280·7,01/(7,01 +1) = 490 мм,
b4 – ширина колеса
b4 = ψbaaw = 0,20·280 = 56 мм.
m > 2·6,8·722,2·103/490·56·199 = 1,80 мм,
в открытых передачах расчетное значение модуля увеличивают на 30%, поэтому принимаем по ГОСТ 9563-60 m = 2,5 мм.
Основные геометрические размеры передачи
Суммарное число зубьев:
zc = 2aw/m = 2·280/2,5 = 224
Число зубьев шестерни:
z3 = zc/(u+1) = 224/(7,01+1) =28
Число зубьев колеса:
z4 = zc – z3 = 224 – 28 = 196
 Фактическое передаточное число:
Фактическое передаточное число:
u = z4/z3 = 196/28 = 7,0.
Фактическое межосевое расстояние:
aw = (z3+z4)m/2 = (196+28)·2,5/2 = 280 мм.
делительные диаметры
d3 = mz13 = 2,5·28 = 70 мм,
d4 = 2,5·196 = 490 мм,
диаметры выступов
da3 = d3+2m = 70+2·2,5 = 75 мм
da4 = 490+2·2,5 = 495 мм
диаметры впадин
df3 = d3 – 2,5m = 70 – 2,5·2,5 = 64 мм
df4 = 490 – 2,5·2,5 = 484 мм
ширина колеса
b4 = ybaaw = 0,20·280 = 56 мм
ширина шестерни
b3 = b4 + 5 = 56+5 = 61 мм
Окружная скорость
v = ω2d3/2000 = 31,6·70/2000 = 1,11 м/с
Принимаем 8-ую степень точности.
Силы действующие в зацеплении
- окружная
Ft2 = 2T2/d3 = 2·110,7·103/70 = 3162 H
- радиальная
Fr2 = Ft2tga = 3162tg20º = 1150 H
Расчетное контактное напряжение
 ,
,
где К = 436 – для прямозубых колес [1c.61],
 КНα = 1 – для прямозубых колес,
КНα = 1 – для прямозубых колес,
КНβ = 1,0 – для прирабатывающихся зубьев,
КНv = 1,04 – коэффициент динамической нагрузки [1c.62].
σH = 436[3162(7,00+1)1,0·1,0·1,04/(490·56)]1/2 = 427 МПа.
Перегрузка (427 – 417)100/417 = 2,4% допустимо 5%.
Расчетные напряжения изгиба
σF4 = YF4YβFtKFαKFβKFv/(mb2),
где YF4 – коэффициент формы зуба,
Yβ = 1 – для прямозубых колес,
KFα = 1,0 – для прямозубых колес,
KFβ = 1 – для прирабатывающихся зубьев
KFv = 1,13 – коэффициент динамической нагрузки [1c.64].
Коэффициент формы зуба:
при z3 = 28 → YF3 = 3,84,
при z4 = 196 → YF4 = 3,62.
σF4 = 3,62·1,0·3162·1,0·1,0·1,13/2,5·56 = 92 МПа < [σ]F4
σF3 = σF4YF3/YF4 = 92·3,84/3,62 = 98 МПа < [σ]F3.
Так как расчетные напряжения σH < [σH] и σF < [σ]F, то можно утверждать, что данная передача выдержит передаваемую нагрузку и будет стабильно работать в нормальных условиях весь срок службы.
6  Нагрузки валов редуктора
Нагрузки валов редуктора
Силы действующие в зацеплении конической передачи
окружная
Ft1 = Ft2 = 1478 Н
радиальная для шестерни, осевая для колеса
Fr1 = Fa2 = 307 H
осевая для шестерни, радиальная для колеса
Fa1= Fr2 = 1182 H
Консольная сила от муфты действующая на быстроходный вал
Fм = 100·Т11/2 = 100·36,71/2 = 606 Н
Консольные силы действующие на тихоходный вал
- окружная
Ft2 = 3162 H
- радиальная
Fr2 =1150 H

 Рис. 6.1 – Схема нагружения валов конического редуктора
Рис. 6.1 – Схема нагружения валов конического редуктора
7  Разработка чертежа общего вида редуктора.
Разработка чертежа общего вида редуктора.
Материал быстроходного вала – сталь 45,
термообработка – улучшение: σв = 780 МПа;
Допускаемое напряжение на кручение [τ]к = 10÷20 МПа
Диаметр быстроходного вала

где Т – передаваемый момент;
d1 = (16·36,7·103/π10)1/3 = 26 мм
Ведущий вал редуктора соединяется с помощью стандартной муфты с валом электродвигателя диаметром dдв= 32 мм,
d1 = (0,8¸1,2)dдв = (0,8¸1,2)32 = 25¸38 мм
принимаем диаметр выходного конца d1 = 28 мм;
длина выходного конца:
l1 = (1,0¸1,5)d1 = (1,0¸1,5)28 = 28¸42 мм,
принимаем l1 = 40 мм.
Диаметр вала под уплотнением:
d2 = d1+2t = 28+2×2,2 = 32,4 мм,
где t = 2,2 мм – высота буртика;
принимаем d2 = 35 мм:
длина вала под уплотнением:
l2 » 0,6d2 =0,6×35 = 21 мм.
Диаметр вала под подшипник:
d4 = d2 = 35 мм.
Вал выполнен заодно с шестерней
 Диаметр выходного конца тихоходного вала:
Диаметр выходного конца тихоходного вала:
d1 = (16·110,7·103/π20)1/3 = 30 мм
принимаем диаметр выходного конца d1 = 30 мм;
Диаметр вала под уплотнением:
d2 = d1+2t = 30+2×2,2 = 34,4 мм,
где t = 2,2 мм – высота буртика;
принимаем d2 = 35 мм .
Длина вала под уплотнением:
l2 » 1,25d2 =1,25×35 = 44 мм.
Диаметр вала под подшипник:
d4 = d2 = 35 мм.
Диаметр вала под колесом:
d3 = d2 + 3,2r = 35+3,2×2,5 = 43,0 мм,
принимаем d3 = 45 мм.
Выбор подшипников
Предварительно назначаем радиально-упорные роликоподшипники легкой серии №7207 для быстроходного вала и тихоходного вала.
| Условное обозначение подшипника | d мм | D мм | B мм | С кН | С0 кН | е | Y |
| №7207 | 48,4 | 32,5 | 0,37 | 1,62 |
Эскизная компоновка устанавливает положение колес редукторной пары, элемента открытой передачи и муфты относительно опор (подшипников); определяет расстояния lб и lт между точками приложения реакций подшипников быстроходного и тихоходного валов, а также точки приложения силы давления элемента открытой передачи и муфты на расстоянии lоп и lм от реакции смежного подшипника.
 Выбираем способ смазывания: зубчатое зацепление смазывается за счет окунания шестерни в масляную ванну; для подшипников пластичный смазочный материал. Камеры подшипников отделяем от внутренней полости мазеудерживающими кольцами.
Выбираем способ смазывания: зубчатое зацепление смазывается за счет окунания шестерни в масляную ванну; для подшипников пластичный смазочный материал. Камеры подшипников отделяем от внутренней полости мазеудерживающими кольцами.
Проводим горизонтальную осевую линию – ось ведущего вала; затем проводим вертикальную линию - ось ведомого вала. Из точки пересечения проводим под углом 17,61º осевые линии делительных конусов и откладываем на них отрезки Re = 94 мм.
Вычерчиваем шестерню и колесо, причем ступицу колеса располагаем несимметрично.
Вычерчиваем внутреннюю стенку корпуса:
- принимаем зазор между торцом ступицы и внутренней стенкой корпуса 10 мм;
- принимаем зазор между окружностью вершин зубьев колеса и внутренней стенкой корпуса 12 мм;
При установке радиально-упорных подшипников необходимо учитывать, что радиальные реакции считают приложенными к валу в точках пересечения нормалей, проведенных к серединам контактных площадок.
Для конических роликоподшипников поправка а:
а = В/2 + (d+D)e/6 = 17/2+(35+72)∙0,37/6 = 15 мм.
В результате этих построений получаем следующие размеры:
быстроходный вал: lм = 106 мм; lб = 95 мм: b = 48 мм;
тихоходный вал: с1 = 43 мм: с2 = 58 мм; lоп = 85 мм.
8  Расчетная схема валов редуктора
Расчетная схема валов редуктора
Быстроходный вал

Рис. 8.1 Расчетная схема быстроходного вала.
Горизонтальная плоскость:
åmA = 143Ft1 – 95RBx +106Fм = 0,
RВх = (106·606+143·1478)/95 = 2901 Н
 åmB= 48Ft1 + 201Fм – 95RAx = 0,
åmB= 48Ft1 + 201Fм – 95RAx = 0,
RAx = (201·606 + 48·1478)/95 = 2029 H
Проверка
ΣХ = 0; Fм + RBx – Ft – RAx = 606+2901 – 1478 – 2029 = 0
Изгибающие моменты в горизонтальной плоскости:
Mx1 =1478×48 = 70,9 H×м.
Mx2 = 606×106 = 64,2 H×м.
Вертикальная плоскость:
åmA = 143Fr – 95RBy – Fad1/2 = 0,
RBy = (143·307 – 1182·49,68/2)/95 =153 H,
åmB = 48Fr + 95RAy – Fad1/2 = 0,
RAy = (1182·49,68/2 – 48·307)/95 =154 H
Проверка
ΣY = 0; ; RAy – Fr + RBy = 154– 307 +153 = 0
Изгибающие моменты в вертикальной плоскости:
My1=154·95 =14,6 Н×м,
My2=154·143 +153·48 = 29,4 Н×м,
Суммарные реакции опор:
RА = (20292+1542)0,5 = 2035 H,
RВ = (29012+1532)0,5 = 2905 H,
 8.2 Тихоходный вал
8.2 Тихоходный вал
Силы действующие в зацеплении:
Ft1= 1478 H; Fr2=1182 H; Fa2=307 H.
Ft3=3162 H; Fr3=1150 H.

Рис. 8.2 Расчетная схема тихоходного вала.
 Горизонтальная плоскость:
Горизонтальная плоскость:
åmC = 58Ft2 – 85Ft3 + 101RDx = 0,
RDx = (3162·85 – 58·1478)/101 =1812 H,
åmD = 43Ft2 + 186Ft3 – 101RCx = 0,
RCx = (43·1478 + 186·3162)/101 = 6452 H
Проверка
ΣХ = 0; Ft2 + Ft3 – RCx + RDx = 1478+3162 – 6452 +1812 = 0
Изгибающие моменты в горизонтальной плоскости
Mx1 = 1812·43 = 77,9 H×м.
Mx2 = 3162×85 = 268,8 H×м.
Вертикальная плоскость:
åmC= 58Fr2 + 85Fr3 – 101RDy – Fr2d2/2 = 0,
RDy = (58·1182+85·1150– 307·154,26/2)/101 =1412 H,
åmD = 43Fr2 – 186Fr3 + 101RCy + Fr2d2/2 = 0,
RCy = (186·1150– 43·1182– 307·154,26/2)/101 =1380 H,
Проверка
ΣY = 0; Fr2 – Fr3 – RDy + RCy =1182 –1150 –1412 +1380 = 0
Изгибающие моменты в вертикальной плоскости
My1 =1412∙43 = 60,7 Н×м,
My2 = 1150×85 = 97,8 Н×м,
My3 = 1150×143 –1380·58 = 84,4 Н×м,
Суммарные реакции опор:
RC = (64522+13802)0,5 = 6598 H,
RD = (18122+14122)0,5 = 2297 H,
9  Проверочный расчет подшипников
Проверочный расчет подшипников
Быстроходный вал
Эквивалентная нагрузка
P = (XVFr + YFa)KбКТ
где Х – коэффициент радиальной нагрузки;
Y – коэффициент осевой нагрузки;
V = 1 – вращается внутреннее кольцо;
Kб = 1,3 – коэффициент безопасности при кратковременных перегрузках [c.133];
КТ = 1 – температурный коэффициент.
Осевые составляющие реакций опор:
SA = 0,83eRA = 0,83·0,37×2035 = 625 H,
SB = 0,83eRB = 0,83·0,37×2905 = 892 H.
Результирующие осевые нагрузки:
FaA = SA = 625 H,
FaB = SA + Fa = 625+1182 = 1807 H.
Проверяем наиболее нагруженный подшипник B.
Отношение Fa/Fr =1807/2905=0,63 > е; следовательно Х=0,40 Y=1,62
Р = (0,40×1,0×2905+1,62·1807)1,3×1,0 = 5316 Н.
Требуемая грузоподъемность подшипника:
Стр = Р(573wL/106)1/3333=
= 5316(573×99,5×16000/106)1/3333 = 41,1 кH < C = 48,4 кН
Условие Стр < C выполняется , значит намеченный подшипник №7207 подходит.
Расчетная долговечность подшипника.
 = 106(48,4×103 /5316)3,333/60×950 = 27627 часов, > [L]
= 106(48,4×103 /5316)3,333/60×950 = 27627 часов, > [L]
больше ресурса работы привода, равного 16000 часов.

Тихоходный вал
Эквивалентная нагрузка
Осевые составляющие реакций опор:
SC = 0,83eRC = 0,83×0,37×6598 = 2026 H,
SD = 0,83eRD = 0,83×0,37×2297 = 705 H.
Результирующие осевые нагрузки:
FaC = SC= 2026 H,
FaD = SC + Fa = 2026 + 307 = 2333 H.
Проверяем подшипник C.
Отношение Fa/Fr = 2026/6598= 0,31< e, следовательно Х=1,0; Y= 0
Р = (1,0×1,0×6598 +0)1,3×1,0 = 8577 Н.
Проверяем подшипник D.
Отношение Fa/Fr = 2333/2297= 1,03> e, следовательно Х=0,4; Y= 1,62
Р = (0,4×1,0×2297 +1,62·2333)1,3×1,0 = 6108 Н
Дальнейший расчет ведем по наиболее нагруженному подшипнику С
Требуемая грузоподъемность подшипника:
Стр = Р(573wL/106)1/3=
= 8577(573×31,6×16000/106)1/3,333 = 47,0 кH < C = 48,4 кН
Расчетная долговечность подшипника.
 = 106(48,4×103 /8577)3,333/60×302 = 17654 часов, > [L]
= 106(48,4×103 /8577)3,333/60×302 = 17654 часов, > [L]
больше ресурса работы привода, равного 16000 часов.
Условие Стр < C и Lh > L выполняется , значит намеченный подшипник №7207 подходит.