Суть і завдання дисперсійного аналізу
Тема 7.
Дисперсійний аналіз
Суть і завдання дисперсійного аналізу
Принципова схема дисперсійного аналізу.
Особливості дисперсійного аналізу соціально-економічних явищ.
Суть і завдання дисперсійного аналізу
В епоху бурхливого, і досить часто не прогнозованого, розвитку суспільства використання методів математичної статистики в соціально-економічних дослідженнях стає нагальною вимогою та необхідністю. Слід визнати, що останнім часом широкого застосування у багатофакторному аналізі набув кореляційно-регресійний метод. І в то й же час майже зовсім не використовується досить ефективний засіб статистико-математичної обробки даних дослідження – дисперсійний аналіз. Як і інші ймовірносно-статистичні методи, він набагато розширює можливості стратегів економічної сфери в аналізі соціально-економічних явищ та процесів та значно підвищує рівень наукових досліджень.
Дисперсійний аналіз розроблений та вперше введений в практику сільськогосподарських та біологічних досліджень англійським вченим Р.А. Фішером, який відкрив закон розподілу відношень середніх квадратів (дисперсій) і в подальшому суттєво доповнений працями Іейтса. У нашій країні перший опис основ дисперсійного аналізу здійснено у 1933 р. М.Ф. Деревицьким у додаткових розділах до підручника В. Іогансена "Елементи точного вчення про змінюваність та спадковість".
Дисперсія або варіанса (σ2, ms) – середній квадрат відхилень, відношення суми квадратів відхилень значень окремих варіантів від середньої для даного варіаційного ряду до числа ступенів свободи (n): 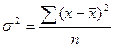 - проста, або зважена -
- проста, або зважена - 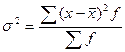 , (σ2 характеризує загальну мінливість вибірки за даною кількісною ознакою).
, (σ2 характеризує загальну мінливість вибірки за даною кількісною ознакою).
Отже, дисперсійний аналіз (аналіз варіанс) – математичний аналіз розсіювання (варіювання) даних, при якому встановлюється роль окремих факторів або їх взаємодія в мінливості (варіації) тієї або іншої враховуваної в спостереженні ознаки.
Дисперсійний аналіз широко використовується для планування досліду та статистичного аналізу отриманих даних. Якщо в недалекому минулому вважали. що роль математика в тім, щоб тільки в аналізі експериментальних даних, то праці Р.А. Фішера корінним чином змінили цю точку зору, і в даний час статистичне планування досліду в відповідності з вимогами дисперсійного аналізу і математична інтерпретація результатів - обов'язкові умови успішного отримання відповідей на питання. що цікавлять дослідника. Статистично обґрунтований план досліду визначає і метод математичного аналізу результатів. тому сучасний дослід неможливо вірно спланувати, не знаючи основ дисперсійного аналізу.
При дисперсійному аналізі одночасно обробляють дані декількох вибірок (варіантів), що складають єдиний статистичний комплекс, оформлений в вигляді спеціальної робочої таблиці. Структура статистичного комплексу та його послідуючий аналіз визначається схемою і методикою експерименту.
Головне призначення дисперсійного аналізу – статистично виявити вплив різних факторів на мінливість ознаки, що вивчається. Особливий інтерес являє використання цього методу в аналізі економічних процесів та явищ, коли мінливість результативної ознаки викликана одночасно дією кількох факторів, сила впливу яких різна. Зокрема з таким положенням ми зустрічаємося при аналізі результативних синтетичних показників економічної ефективності виробництва. Найкращий ефект тут дає одночасний дисперсійний аналіз всіх відібраних факторів – багатофакторний аналіз.
Можна, звичайно, зробити і попарне порівняння факторів, при якому всі інші фактори ігноруються. але такий підхід до розв'язання питання не дає можливості виявити існуючу в дійсності множинність ефектів взаємодії.
Прийняття на озброєння економістів дисперсійного методу дозволяє розв'язувати досить важливі завдання, виходячи з сучасних вимог до рівня економічного аналізу. У сфері соціально-економічних досліджень цей досить ефективний статистико-математичний засіб повинен зайняти одне з ключових місць комплексного факторного аналізу. перш за все тому, що використання дисперсійного методу може мати самостійне значення.
Суть дисперсійного аналізу полягає в розкладанні загальної суми квадратів відхилень і загального числа ступенів свободи на частини – компоненти, що відповідають структурі досліду і оцінці достовірності дії та взаємодії вивчаємих факторів за F – критерієм.
В основі цього методу лежать слідуючі властивості:
Ä замість індивідуальних помилок групових середніх, тобто середніх кожного варіанту, обчислюють одну усереднену помилку загальної вибірки, яку використовують для оцінки різниці між варіантами.
Ä середню помилку досліду знаходять шляхом розкладу загальної дисперсії (варіювання) всіх даних досліду на складові частини, що характеризують варіювання вивчаємих в досліді факторів і варіювання випадкове, джерелом якого являється не контролюєма дослідником багатогранність впливу зовнішніх умов на мінливість вивчаємих ознак і властивостей.