Общие сведения. Физические основы эксперимента
Лабораторная работа №1. ПРИМЕНЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ СКОРОСТИ ПОЛЕТА ПУЛИ
Цель работы: проведение экспериментального определения скорости полета пули с использованием законов сохраненияимпульса, механической энергии и момента импульса.
Вариант 1. Определение скорости полета пули на баллистическом маятнике
Описание лабораторной установки и оборудования
Баллистический маятник – это коробка 1, заполненная пластилином, подвешенная на четырех длинных нитях (на рисунке 1.1 нити изображены не в масштабе).
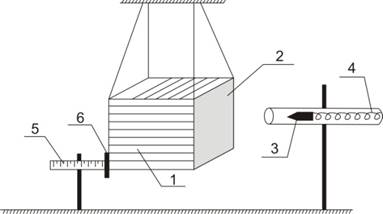
Рис.1.1
Боковая поверхность пластилина 2 открыта, так что там может застревать пуля 3, выстреливаемая из пружинного пистолета 4. После выстрела маятник вместе с пулей отклоняется на некоторый угол и передвигает движок 6, установленный на линейке 5. Масса пули значительно меньше массы маятника, поэтому угол отклонения мал. Массу маятника можно увеличивать, вкладывая в коробку металлические пластины известной массы.
Общие сведения. Физические основы эксперимента
Для описания физических процессов в данной лабораторной работе используются следующие законы:
1. Закон сохранения импульса: Если на систему тел не действуют внешние силы (такая система называется замкнутой) или их векторная сумма равна нулю, то суммарный импульс системы остается постоянным.
Если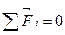 
, то 
.
Если сумма внешних сил не равна нулю, но равна нулю проекция всех сил на какое-либо направление, то сохраняется проекция суммарного импульса на это направление.
Если 
, то 
.
2. Закон сохранения механической энергии: Если в замкнутой системе между телами действуют только консервативные силы (силы упругости, тяжести, кулоновские), то полная механическая энергия системы (сумма кинетических и потенциальных энергий всех тел) остается постоянной.
Если в системе есть диссипативная сила (трение, пластическая деформация), то уменьшение полной механической энергии равно работе этой силы. Часть механической энергии, равная работе диссипативной силы, переходит при этом в тепловую энергию.
Далее мы покажем, как применить эти законы сохранения в данном лабораторном эксперименте, и как использовать полученные уравнения, для определения скорости полета пули.
Рис.1.2
На рисунке 1.2 показаны последовательные состояния системы «пуля + маятник» после выстрела:
2.1. Пружина пистолета сжата, пуля лежит в стволе. Полная механическая энергия 
равна потенциальной энергии 
сжатой пружины. Кинетическая энергия системы 
.
2.2. Пуля после выстрела летит к маятнику. Полная энергия системы равняется кинетической энергии пули:
.
Импульс системы равен импульсу пули:
.
где 
- масса пули,
- скорость пули.
В нашем рассмотрении мы пренебрегаем небольшой вертикальной составляющей скорости, возникающей из-за действия силы тяжести.
2.3. Пуля застряла в маятнике (неупругий удар). Маятник, получив удар, приобретает скорость 
и начинает отклоняться от положения равновесия. Часть кинетической энергии пули уходит на работу по деформации пластилина. Полная механическая энергия уменьшилась и стала равной:
.
Импульс системы:
,
где 
- масса маятника;
- скорость маятника сразу после удара пули.
2.4. Маятник с пулей отклонился на угол 
, центр тяжести поднялся на высоту 
. Кинетическая энергия в верхней точке равна нулю. Полная энергия состоит только из потенциальной:
.
Из рисунке 2.4 : 
, 
.
При малых углях 
можно считать: 
,
Тогда
(1.1)
Рассмотрим состояния 2.2 и 2.3 (до и после удара). Полная энергия при переходе от 2.2 к 2.3 не сохраняется, однако сохраняется импульс системы в проекции на горизонтальное направление, т.к. проекции силы тяжести и силы натяжения нити (внешние силы) на это направление равны нулю:
или 
,
отсюда
. (1. 2)
Рассмотрим состояние 2.3 и 2.4. Поскольку сила трения на маятник не действует, то по закону сохранения энергии 
,
или
.
Отсюда
. (1.3)
Подставив (1.1) в (1.3) и (1. 3) в (1.2) получим:
. (1. 4)
Формула (1.4) используется для экспериментального определения скорости полета пули в данной лабораторной работе.