For the period of oscillations of scope without loads have

ВСТУП

 

Основна спрямованість методичних вказівок з предмету фізика - дати можливість студентам за допомогою досліду вивчити важливі фізичні явища. Опис лабораторних робіт не претендує на те, щоб створити у студентів повне уявлення про явища, які вивчаються. Таке уявлення може виникнути лише внаслідок опрацювання лекцій та підручників.

Велика увага в методичних вказівках з фізики для студентів технічних спеціальностей приділяється обробленню результатів вимірювання. Для успішного виконання робіт необхідна попередня самостійна підготовка, в першу чергу теоретична.

Кожна лабораторна ро­бота розрахована на дві академічні години занять у лабораторії. Перед заняттям студент повинен підготувати протокол ла­бораторної роботи, вивчивши відповідний теоретичний матері­ал.

Під час заняття студенти проводять необхідні виміри, виконують розрахунки, доводять звіт до висновку. Результати вимірювання обговорюються з викладачем і затверджуються.

Повністю оформлений звіт по лабораторній роботі потрібно подати виклада­чу до кінця заняття. Він повинен містити: титульний лист, номер лаборато­рної роботи та її назву, перелік приладів і приладдя, мету робо­ти, схему установки, розрахункові формули, таблицю результа­тів вимірів і розрахунки, висновки за результатами роботи. Графіки повинні бути виконані на мі­ліметровому папері.

Якщо студент не встигає захистити лабораторну роботу до кінця заняття, дозволяється оформити звіт (графіки) з використанням комп’ютерних програм (Excel, Origin) до наступного заняття.

Лабораторна робота вважається виконаною після успішно проведеного захисту шляхом співбесіди студента з викладачем (захист звіту + оцінка за теоретичний матеріал).

Захист звіту: мета роботи + експериментальна методика + висновки.

Теоретичний матеріал: знання фізичних явищ, які вивчалися у даній лабораторній роботі (закони, формули).

INTRODUCTION

 

Basic goal of the laboratory work manual on Physics is to enable students to learn important physical phenomena by experience. Laboratory work description does not try to give students a complete picture of the studied phenomena. Such presentation can only be achieved as a result of study of lectures and textbooks.

Large attention in the laboratory work manual on Physics for the students of technical professions is devoted to the handling of the measured results. Prior independent preparation, above all theoretical, is needed for successful completion of the work.

Every laboratory work is supposed to take two academic hours. Before the class a student must prepare a protocol of laboratory work and learn appropriate theoretical material.

During the class students do the necessary measurements, execute calculations and take the report to the conclusion. Measured results are discussed with a teacher and confirmed.

Fully designed report on laboratory work should be given to the teacher before the end of the class. It must include: title sheet, laboratory work number and name, list of devices and installations, purpose of work, drawing of the setting, calculation formulae, table of the measurement results and calculations, conclusions, as the result of the work. Graphs must be done on a millimeter`s paper.

If a student does not have time to support the laboratory work before the end of the class, he/she is allowed to design a report (graph) with the use of the computer programs (Excel, Origin) for the next class.

Laboratory work is considered done after the successful speech in support in front of a teacher (report explanation + mark for theoretical material).

Support of report: purpose of work + experimental method + conclusions.

Theoretical material: knowledge of the physical phenomena, which was studied in this laboratory work (laws, formulas).

ЛАБОРАТОРНА РОБОТА № 43.5

Крутильний маятник

Мета роботи:Вивчення законів коливаннякрутильного маятника.

Завдання:а) перевірити залежність періоду вільних коливань

крутильного маят­ника від його моменту інерції.

б) перевірити формулу для моменту інерції кулі (стержня).

Прилади і обладнання: крутильний маятник, штангенциркуль, набір циліндрів або стержнів, куля.

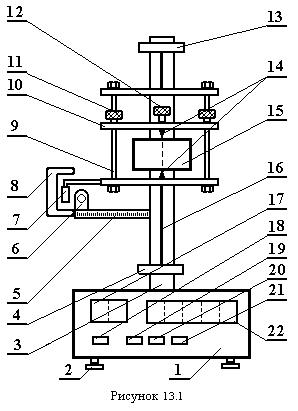Експериментальна установка (рис.13.1) складається із основи 1, вирівню­вання якої здійснюється ніжками 2. В основі закріплена стійка 3, на якій фік­сується нижній кронштейн 4 і верхній 13. На цих кронштейнах на стальному дроті 16 підвішена рамка 9, яка має ру­хому планку 10 з двома фіксуючими цанговими гайками 11. В рамці на двох центруючих штиф­тах 14 кріпиться досліджуване тіло 15 (циліндр, сте­р­жень, куб, куля) і затискується

гвинтом 12. До рамки прикріплений прапо­рець 7, який, перетинаючи світловий промінь фо­то­електричного датчика 8, вмикає електронну систему підрахунку кі­лькості коливань (індикатор 17) та секундомір (індикатор 22). За допо­могою цього прапорця рамка фіксу­ється у початковому положенні елект­ромагнітом 6 при певному куті повороту, який вимірюється по шкалі 5. На передній панелі приладу знаходяться: вимикачі 18 – “СЕТЬ”, 19 – “СБРОС”, 20 “ПУСК” 21 – “СТОП”.

Теоретична частина

Крутильний маятник (рис.13.2) – це тіло, яке може обертатись відносно довільної осі під дією пружної сили, що виникає при деформації кручення дроту, на якому закріплене тіло. Запишемо основне рівняння динаміки обертального руху ,(13.1)

деI- момент інерції тіла, – кутове

 

прискорення. При деформації кручення дроту момент

 

сили пропорційний куту закручування, тобто

(13.2)

Знак мінус враховує, що момент сили зменшує кут повороту α.Одержуємо диференціальне рівняння коливань крутильного маятника

. (13.3)

Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань , (13.4)

одержуємо циклічну частоту та період коливань крутильного маятника

. (13.5)

Для виконання першого пункту завдання необхідно змінювати момент інерції маятника. Це здійснюється заміною тіл, які закріплюються в рамці 9. Для цього використовується комплект вантажів з різними геометричними розмірами, але з однаковою масою.

Момент інерції циліндра відносно його осі

. (13.7)

Момент інерції стержня відносно осі, яка перпендикулярна до нього і проходить через його середину

. (13.8)

Момент інерції кулі відносно діаметра

. (13.9)

Підстановка цих виразів у формулу (13.5), з урахуванням моменту інерції рамки Ip та адитивності моменту інерції, дає можливість обчислити періоди коливань:

циліндра , (13.10)

стержня , (13.11)

 

кулі . (13.12)

Піднісши вирази (13.10), (13.11) і (13.12) до квадрату, одержуємо:

 

~ R2, (13.13)

 

~L2, (13.14)

 

~ R2, (13.15)

Із формул (13.13) ÷ (13.15) видно, що квадрати періодів коливань пропорційні квадратам відповідних характерних геометричних розмірів тіл (радіусу, довжини).

Для періоду коливань рамки без вантажів маємо

. (13.16)

Замінюючи у виразах (13.13) - (13.15) перші доданки виразом (13.16), одержуємо

, (13.17)

 

~ L2, (13.18)

 

~ R2. (13.19)

Таким чином, залежності квадратів періодів від квадратів відповідних характерних розмірів за теорією повинні бути лінійними. Причому відрізок, який відсікає графік на осі ординат (квадратів періодів) дорівнює квадрату періоду коливань вільної рамки, а тангенс кута нахилу графіків залежить від коефіцієнта пропорційності k між обертаючим моментом та кутом α (див. формулу (13.2)). Експериментально досліджується залежність між періодом коливань Т крутильного маятника та радіусом циліндрів (довжиною стержнів). Будується графік в координатах Т2 = f(R2) для циліндрів, чи Т2 = f(L2) для стержнів. Якщо графік буде прямолінійний, то це якісно підтверджує справедливість теоретичних формул (13.17) і (13.18), а співпадання значень, які відсікають ці графіки на осі ординат, з квадратом періоду рамки кількісно підтверджують справедливість цих формул. Крім цього, по тангенсу кута нахилу вказаних графіків можна знайти коефіцієнт k, а точніше відношення m/k2, і за формулою (13.19) розрахувати період коливань Тк. Якщо це розрахункове значення буде близьким до безпосередньо виміряного, це підтвердить справедливість теоретичних формул, і зокрема, формули (13.9).

 

Практична частина

 

1. Увімкнути вилку живлення в мережу 220 В і натиснути вимикач „СЕТЬ”.

2. Натиснути вимикач “СБРОС”. Обережно повернути рамку до її фіксації за рахунок протягування прапорця 7 електромагнітом 6.

3. Натиснути вимикач „ПУСК”. Електромагніт відпустить рамку, і вона почне здійснювати крутильні коливання. Електронний блок буде відраховувати кількість повних коливань та час коливань.

4. Коли на індикаторі кількості коливань з’явиться цифра 9, натиснути вимикач “СТОП”. Після закінчення 10-го коливання секундомір зу­пи­ниться.

5. Визначити період коливань, поділивши час на кількість коливань, тобто на 10.

6. Відтиснути вимикач “ПУСК”. Виконати вимірювання періоду коливань Тр згідно з пунктами 2 ÷ 5 три рази. Результати занести в таблицю 13.1.

 

Таблиця 13.1

№ п/п Трі, с ΔТрі, с (ΔТрі)2, с2
     
     
     
  =   ∑(ΔТрі)2=

 

7. Виміряти штангенциркулем діаметри циліндра (довжину стержня) і кулі. Обережно, щоб не перервати дріт, закріпити вантаж у рамці. Для цього відпустити цангові гайки 11, перемістити планку 10 вверх, чи вниз, щоб центруючі штифти 14 потрапили в отвори на вантажі. Закрутити цангові гайки і затиснути вантаж гвинтом 12. Циліндр кріпити вздовж його осі, стержень - перпендикулярно до площини рамки.

8. Аналогічно пунктам 2 ÷ 5 виміряти період коливань по одному разу для всіх вантажів, у тому числі і для кулі. Результати вимірів занести в таблицю 13.2.

 

Таблиця 13.2

№ п/п R (L), мм Т, с Т2, с2 R2 (L2), мм2
       
       
       
       
       
Куля        

 

9. Побудувати графік залежності T2 = f(R2), або T2 = f(L2). Продовжити графік до перетину з віссю ординат і по відрізку, який відсікається на ній, визначити квадрат періоду коливань вільної рамки .

10. На прямолінійній частині графіка (рис.13.3) подалі од­на від другої вибрати дві точки 1 і 2. Визначити їх координати по осям, але не із таблиці. Знайти тангенс кута φ нахилу графіка за формулою

 

, (13.20)

 

або . (13.21)

11. За формулами (13.17), (13.20) для циліндрів, або (13.18), (13.21) для стержнів розрахувати числове значення

. (13.22)

12. Підставивши одержане значення, а також середнє значення із таблиці 1 у формулу (13.19), розрахувати квадрат періоду коливань кулі і порівняти його з безпосередньо виміряним (див. таблицю 13.2).

13. Визначити значення ординати, яку відсікає графік T2 = f(R2). Порівняти це значення з квадратом періоду коливань рамки .

14. Зробити висновок що до виконання законів коливань крутильного маятника, а також про справедливість формул для моментів інерції циліндра, стержня, кулі.

 

Контрольні запитання

 

1. Що таке крутильний маятник?

2. Складіть та запишіть диференціальне рівняння вільних гармонічних коливань крутильного маятника.

3. Запишіть рівняння коливань, яке є рішенням диференціального рівнян­ня гармонічних коливань. Накресліть графік цього рівняння.

4. Як називають величини, що входять в рівняння коливань крутиль­ного маятника. Які розмірності цих величин?

5. Запишіть формули для періоду та циклічної частоти коливань крутильного маятника.

 

Література

 

1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.

2. Лапотинський І.Е., Зачек І.Р. Фізика для інженерів.- Львів: Афіша, 2003.-С.

3. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.

4. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.

 

Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К.

 

 

LABORATORY WORK № 43.5

TORSION PENDULUM

 

Purpose of work is to study of laws of oscillations of the torsion pendulum.

Task: check up dependence of period of free oscillations torsion pendulum from its moment of inertia; check up a formula for the moment of inertia of ball (peg).

Devices and equipments: torsion pendulum, set of cylinders or pegs, balls.

 

Figure 14.1

 

The experimental setting (fig.14.1) consists of basis 1. In basis a peg is fastened 3, on what fix lower bracket 4 and overhead 13. On these brackets on a steel wire 16 the suspended scope 9, which has a moving slat 10 with two fixative nuts 11. In a scope on two centrings dowels 14 the probed body is fastened 15 (cylinder, peg, cube, ball) and it is compressed spirally 12. On a scope small flag is fastened 7, which, crossing the light ray of photoelectric sensor 8, includes the electronic system of count of amount oscillations (indicator 17) and stop-watch (indicator 22). After help of this small flag a scope of fix is in initial position of electromagnet 6 at certain corner of turn which is measured on a scale 5. On the front panel of device are: switches 18 – “Сеть'”, 19 – “Срос”, 20 “Пуск” 21 – “FEET”.

 

Theoretical part

 

A turning pendulum is a body, which can be revolved in relation to an arbitrary axis under the action of resilient force, which arises up during deformation of twisting of wire, which the fastened body is on. Write down the fundamental equation of the rotational motion dynamics

(14.1)

where I is a moment of inertia of body, is an angular acceleration. During deformation of twisting of wire the moment of force is proportional the corner of rollup, that

(14.2).

Figure 14.2

 

A sign does minus take into account, that the moment of force is diminished by the corner of turn α. Get differential equation of oscillations of the turning pendulum

. (14.3)

Comparing this equation to general equation of undamped harmonic oscillations

, (14.4)

get cyclic frequency and period of oscillation of the turning pendulum

. (14.5)

For implementation of the first point of task it is necessary to change the moment of inertia of pendulum. It is carried out replacement of bodies which are fastened in a scope 9. For this purpose the complete set of loads is used with different geometrical sizes, but with identical mass. A moment of inertia of cylinder is in relation to its axis

(14.18).

Moment of inertia of peg in relation to an axis, what perpendicular to it and passes through his middle

(14.8).

A moment of inertia of ball is in relation to a diameter

(14.9).

The substitution of this expressions in a formula (14.5), taking into account the moment of inertia of scope of Ip and additivity of moment of inertia, enables to calculate the periods of oscillations:

cylinder , (14.10)

 

peg , (14.11)

 

balls . (14.12)

Bringing expressions (14.10), (14.11) and (14.12) to the square, get:

 

~ R2 (14.13)

 

~ L2 (14.14)

 

~ R2 (14.15)

 

From formulas (14.13) - (14.15) evidently, that the squares of periods of oscillations are proportional the squares of the proper characteristic geometrical sizes of bodies (radius, length).

For the period of oscillations of scope without loads have

. (14.16)

Replacing in expressions (14.13) are (14.15) the first elements by expression (14.16), get

, (14.17)

 

~ L2 (14.18)

 

~ R2. (14.19)

Thus, dependences of squares of periods on the squares of the proper characteristic sizes after a theory must be linear. Thus segment which chops off a chart on wasp of ordinates (squares of periods) equals the square of period of oscillations of free scope, and does the tangent of angle of slope of graph depend on the coefficient of proportion k between a rotary-type moment and corner α (wonders formula (14.2)). Dependence is experimentally probed between the period of oscillations of T of turning pendulum and radius of cylinders (long pegs). A chart is built in the co-ordinates of T2 = f(R2) for cylinders, whether T2 = f(L2) for pegs. If a graphic will be lineal, then it high-quality confirms justice of theoretical formulas (14.17) and (14.18), and coinciding of values, which chop off this graphic on wasp of ordinates, with the square of period of scope in number confirm justice of these formulas. Except for it, on the tangent of angle of slope of the indicated graph it is possible to find a coefficient k, and more precisely relation of m/k2, and after a formula (14.19) to calculate the period of oscillations of Tk. If it a calculation value will be near to directly measured, it will confirm justice of theoretical formulas, and in particular, formulas (14.9).

 

Practical part

 

1.To plug a device in a network 220 V and to press the switch of „СЕТЬ '”.

2. To press the switch of “СБРОС”. Carefully to turn a scope to its fixing due to reaching of small flag by a 7 electromagnet 6.

3. To press a switch „ПУСК”. An electromagnet will release a scope, and it will begin to carry out turning oscillations. An electronic block will deduct the amount of full oscillations and time of oscillations.

4. When a number 9 will appear on the indicator of amount of oscillations, to press a switch “СТОП”. Upon termination of 10th oscillation stop-watch of stop.

5. To define the period of oscillations, dividing time into the amount of oscillations, that on 10.

6. To push back a switch “ПУСК”. To execute measuring of period of oscillations of Tr in obedience to points 2 ÷ 5 three times. To add results to the table 14.1.

 

Table 14.1

№ T, s   ΔT, s   (ΔT)2, s2  
     
     
     
  =   ∑(ΔТрі)2=

 

Measure a Vernier calipers the diameters of cylinder (length of peg) and ball. Carefully, not to cut a wire short, fasten a load in a scope. For this purpose to release nuts 11, to move a slat 10 up, how downward, that centrings dowels 14.

7. Got in openings on a load. To twirl nuts and clutch a load spirally 12. To fasten a cylinder along his axis, peg - athwart to the plane of scope.

8. Like points 2 ÷ 5 to measure the period of oscillations on once for all loads, including for a ball. To add the results of measurings to the table 14.2.

 

 

Table 14.2.

№ R (L), mm Т, s Т2, s2 R2 (L2), mm2
       
       
       
       
       
Ball          

 

9. To build the chart of dependence of T2 = f(R2), or T2 = f(L2). To continue a chart to crossing with the axis of ordinates and on a segment which is chopped off on it, to define the square of period of oscillations of free scope .

10. On lineal part of graphic (fig.14.2) a little rather one from the second to choose two points 1 and 2. To define their co-ordinates for to the axes, but not from a table. To find the tangent of corner φ to inclination of graphic by formula

 

, (14.20)

 

or . (14.21)

11. After formulas (14.17), (14.20) for cylinders, or (14.18), (14.21) for pegs to calculate a numerical value

. (14.22)

12. Putting the got value, and also mean value , from a table 1 in a formula (14.19), calculate the square of period of oscillations of ball and compare it to directly measured (see a table 14.2).

13. To define the value of ordinate which is chopped off by the graphic T2 = f(R2). To compare this value to the square of period of oscillations of scope.

14. Draw conclusion that to implementation of laws of oscillations of the turning pendulum, and also about justice of formulas for the moments of inertia of cylinder, peg, ball.

 

Figure 14.3

 

Control questions

 

1. What is turning pendulum?

2. Make and write down differential equation of free harmonic oscillations of the turning pendulum.

3. Write down equation of oscillations, which is the decision of differential equation of harmonic oscillations. Draw the graph of this equation.

4. Write down formulas for a period and cyclic frequency of oscillations of the turning pendulum.

 

Literature

 

1. 1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.

2. Лапотинський І.Е., Зачек І.Р. Фізика для інженерів.- Львів: Афіша, 2003.- С.

3. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.

4. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.

 

 

Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.

Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.

 

Approved by the chair of physics. Protocol № 6 from 30.03.2009 .

 

 

ЛАБОРАТОРНА РОБОТА № 43.6

КОЛИВАННЯ ОБРУЧА

Мета роботи: вивчення законів коливанняфізичного маятника. Перевірити формулу періоду коливань фізичного маятника.

Завдання:а) експериментально виміряти період коливань обруча відносно точки підвісу О, яка знаходиться на ньому (рис.15.1);

б) розрахувати теоретичне значення періоду.

Прилади і обладнання: обруч (фізичний маятник), секундомір, лінійка.

Експериментальна установка:на кронштейні 1 підвішений обруч 2.

 

Теоретична частина

Фізичний маятник – це тіло, яке може обертатись відно­сно довільної горизонтальної осі, що не прохо­дить через центр маси. Під дією моменту сили тяжіння mg, плече якої дорівнює L·sinα, тіло обертається навколо точки підвісу О (рис.15.2).L – відстань від точки О обертан­ня (точки підвісу) до точки С - центра маси тіла. Записуємо основне рівняння динаміки обер­тального руху

,(15.1)

 

де I- момент інерції тіла, - кутове прискорення. Знак мінус враховує, що момент сили mg зменшує кут α.Таким чином, одержуємо диференціальне рівняння незатухаючих коливань фізичного маятника

. (15.2)

 

При малих кутах α (менших 5о) можна вважити, що sinα = α. Одержуємо (15.3)

Порівнюючи це рівняння із загальним рівнянням незатухаючих гармонічних коливань , (15.4)

одержуємо циклічну частоту та період коливань фізичного маятника

(15.5)

Таким чином, період коливань фізичного маятника залежить від положення точки підвісу О і форми тіла, тобто його моменту інерції відносно цієї точки. У нашому випадку для обруча L = R, а момент інерції з врахуванням теореми Штейнера дорівнює

. (15.6)

Таким чином період коливання обруча

. (15.7)

Практична частина

1. Привести обруч у коливання, відхиливши його на кут не більший, ніж 5о.

2. У момент, коли обруч знаходиться в одному із крайніх положень, увімкнути секундомір і виміряти час t двадцяти (N=20) коливань.

3. Повторити експеримент згідно з пп. 1 ÷ 2 ще 4 рази (всього 5). Результати занести в таблицю 15.1.

Таблиця 15.1

і , с ,с D,см Tексп,с Tтеор,с
           
     
     
     
     
   

4. Розрахувати середнє значення часу та похибку його вимірювання як прямого 5-ти кратного вимірювання.

5. За формулою знайти експериментальне значення періоду, та його похибку.

6. Зняти обруч із кронштейна і виміряти лінійкою його середній діаметр D.

7. За формулою (15.7) розрахувати теоретичне значення періоду .

8. Співставити одержані значення періодів та зробити висновок.

 

Контрольні запитання

 

1. Що таке фізичний маятник?

2. Складіть та запишіть диференціальне рівняння вільних гармонічних коливань фізичного маятника.

3. Запишіть рівняння коливань, яке є рішенням диференціального рівнян­ня фізичного маятника. Накресліть графік цього рівняння.

4. Як називають величини, що входять в рівняння коливань фізич­ного маятника? Які розмірності цих величин?

5. Запишіть формули для періоду та циклічної частоти коливань фізичного маятника.

6. Сформулюйте теорему Штейнера.

7. Одержати період коливань обруча відносно осі, яка перпендикулярна до його площини проходить через нього.

 

Література

 

1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.

2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.

3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.

 

Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К.

LABORATORY WORK № 43.6

OSCILLATION OF HOOP

 

Purpose of work: study of laws of swing of the physical pendulum. To check up the formula of period of oscillations of the physical pendulum.

Task: 1) experimentally to measure the period of oscillations of hoop in relation to the point of hang up O, which is on it (fig 16.1);

2) calculate the theoretical value of period.

Figure 16.1

 

Devices and equipments: hoop (physical pendulum), stop-watch, line.

Experimental setting: on a bracket a 1 suspended hoop 2.

 

Theoretical part

 

A physical pendulum is a body which can be revolved relatively of arbitrary horizontal axis, that not go through the center of mass. Under the action of moment of force mg, the arm of which is evened L·sinα, a body is revolved round the point of hang up O (fig 16.2). L is distance from a point O rotation (points of hang up) to the point of C - center of mass of body. Write down the fundamental equation of the rotational motion dynamics

, (16.1)

I is a moment of inertia of body, is an angular acceleration. A sign does minus take into account, that the moment of force of mg is diminished by a corner α. Thus, get differential equation of undamped oscillations physical pendulum

(16.2)

At small corners α (less 5о) is it possible, that sin α = α. Get

(16.3)

Comparing this equation to general equation of undamped harmonic oscillations (16.4) get cyclic frequency and period of oscillations of the physical pendulum

(16.5)

Thus, the period of oscillations of the physical pendulum depends on position of point of hang up O and forms of body, that to his moment of inertia in relation to this point. In our case for the hoop of L = R, and the moment of inertia taking into account the theorem of Steiner is evened

. (16.6)

Thus period of oscillation of hoop

. (16.7)

Figure 16.2

Practical part

 

1. To drive a hoop to oscillation, declining him on a corner not greater, than 5о.

2. In moment, when a hoop is in one of extreme positions, to include a stop-watch and measure time of t of twenty (N=20) oscillations.

3. To repeat an experiment in obedience to 1-2 yet 4 times (in all 5). To add results to the table 16.1.

 

Table 16.1

  , s   ,s   D, sm   T, s   T, c  
           
     
     
     
     
   

 

4. Calculate the mean value of time and error of his measuring as direct 5-th multiple measuring.

5. After a formula to find the experimental value of period, and his error.

6. To take off a hoop from a bracket and measure the line of him the middle diameter of D.

7. By formula (16.7) to calculate the theoretical value of period

8. Draw conclusion.

 

Control questions

 

8. What is physical pendulum?

9. Make and write down differential equation of free harmonic oscillations of the physical pendulum.

10. Write down equation of oscillations, which is the decision of differential equation of physical pendulum. Draw the graph of this equation.

11. How does name sizes which are included in equation of oscillations of the physical pendulum? What to the dimension of these sizes?

12. Write down formulas for a period and cyclic frequency of oscillations of the physical pendulum.

13. Formulate the theorem of Steiner.

14. To get the period of oscillations of hoop in relation to an axis, the what perpendicular to his plane passes through it.

 

Literature

 

1. Чолпан П.П. Фізика.- К.: Вища школа, 2003.- С.77-80.

2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.196-199.

3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.222-223.

 

 

Translator: S.P. Lushchin, the reader, candidate of physical and mathematical sciences.

Reviewer: S.V. Loskutov, professor, doctor of physical and mathematical sciences.

 

Approved by the chair of physics. Protocol № 6 from 30.03.2009 .

 

17 ЛАБОРАТОРНА РОБОТА № 44

ЗАТУХАЮЧІ МЕХАНІЧНІ КОЛИВАННЯ

Мета роботи:вивчення характеристик затухаючих коливань.

Завдання: дослідити залежність коефіцієнта затухання пружин­ного маятника від маси тягарця. Методом лінеаризації графіка, пока­зати, що коефіцієнт затухання обернено пропорційний масі тіла.

Прилади і обладнання:пружина, секундомір, лінійка, на­бір тягарців,

диск.

Експериментальна установка(рис.17.1) складається з кронштейна 1, на якому закріплена пружина 2 з державкою 6 для тягарців 4. Деформація пружини вимірюється лінійкою 7, а час коливань маятника –секундоміром 3. На державку 6 підвішується диск 5, який за рахунок опору повітря забезпечує затухання коливань.

 

Теоретична частина

 

Затухаючими називаються такі коливання, амплітуда яких зменшу­ється з часом. Енергія коливальної системи теж зменшується.

Затухаючі коливання описуються диференціальним рівнянням:

, (17.1)

 

де: - зміщення, - коефіцієнт затухання, - циклічна частота незатухаючих вільних коливань, - жорсткість пружини, - маса тягарця, - коефіцієнт опору.

Розв’язок рівняння (17.1) дає закон зміни зміщення від часу:

. (17.2)

Амплітуда затухаючих коливань зменшується з часом по експонен­ціаль­ному закону:

. (17.3)

Затухаючі коливання характеризуються: коефіцієнтом затухання , логариф­мічним декрементом , часом релаксації , добротністю .

Логарифмічним декрементом затухання називається натуральний логарифм від­ношення амплітуд коливань взятих через період:

. (17.4)

Час, за який амплітуда коливань зменшується в е раз, називається

часом релаксації :

. (17.5)

Із (17.5)одержуємо, що або , тобто коефіцієнт затухан­ня обер­нений часу, за який амплітуда коливань зменшується в раз. Вира­зивши в (17.4)через , отримуємо:

. (17.6)

Таким чином, логарифмічний декремент затухання обернений числу коливань , за яке амплітуда зменшується в раз.

Відношення називається добротністю. Вона пропорційна від­ношенню енергії системи до втрати енергії за період.

Якщо система виконала довільну кількість коливань , то середнє значення логарифмічного декременту затухання можна знайти за формулою:

(17.7)

Практична частина

 

1. Підвісити на пружину диск. Маса диска вказана на ньому. Записати координату рівноваги xp в таблицю 17.1.

 

Таблиця 17.1

m, кг кг-1 xp см xo см Ao= =xo-xp см xN   см AN= =xo-xN см t   с N c с-1
                       
                       

 

2. Вивести тягар із положення рівноваги, стиснувши пружину на 6÷10 см. Записа­ти координату x0 тягарця в цьому положенні, відпустити тягар і одно­часно включити секундомір. Підрахувати кількість N коли­вань, протягом яких амплітуда зменшиться в 3-4 рази. Замітити і записати координату xN верхнього положення тягарця в кінці N-го коливан­ня. Зупинити секундомір і записати час N коливань. Результати ви­мірювань і обчислень занести до таблиці 17.1.

3. Комбінуючи тягарцями, повторити 6÷7 разів експеримент і виконати розрахунки згідно пп.1-2. змінюючи загальну масу mмаятника від найменшої (одна державка з диском) до найбільшої (підвішені усі тягарці). Маса державки 11 г, маси тягарців указа­ні на них. Диск при цьому не знімати.

Зауваження: кількість коливань N приблизно дорівнює 50.

4. Побудувати графік залежності .

5. Зробити висновок, як залежить коефіцієнт затухання пружинного маят­ни­ка від маси тягарця і чи узгоджується ця залежність з теоретичними положеннями?

 

Контрольні запитання

1. Які коливання називають затухаючими?

2. Записати диференціальне рівняння затухаючих коливань і вказати фізичний зміст величин, які входять у нього.

3. По якому закону змінюється зміщення затухаючих коливань з ча­сом? Напишіть рівняння затухаючих коливань та намалюйте його графік.

4. Як залежить амплітуда затухаючих коливань від часу?

5. Дати визначення і записати вираз для логарифмічного декремента затухання.

6. Що називається часом релаксації?

7. Який фізичний зміст логарифмічного декремента та коефіцієнта затухання?

8. Дати визначення добротності. Який її фізичний зміст?

9. Записати зв’язок між коефіцієнтом затухання і логарифмічним декрементом затухання.

10. Як залежить коефіцієнт затухання коливань пружинного маятника від маси?

 

Література

 

1. Бушок Г.Ф., Венгер Є.Ф.Курс фізики: ч. 1.- К: Вища школа. 2003, С. 185-188.

2. Савельев И.В. Курс общей физики. - т.1, М.: Наука,1982.- С.204-209.

3. Трофимова Т.И. Курс физики.- М: Высшая школа, 1990.- С.229-234.

Інструкцію склав доцент каф. фізики ЗНТУ Манько В.К.

18 LABORATORY WORK № 44