Порядок оформления контрольной работы
Вопросы к контрольной работе по курсу
«Микроэкономика»
Задание для группы 417511
1. Производственная функция короткого периода: понятие, сущность, графическое изображение. Показатели технической результативности производства в коротком периоде.
2. Производственная функция длительного периода: понятие, сущность и графическое изображение. Предельная норма замещения факторов. Отдача от масштаба.
3. Равновесие производителя: понятие, сущность и графическое изображение. Путь развития фирмы и его зависимость от цен на факторы.
4. Построение функции затрат и семейства кривых затрат короткого периода. Постоянные и переменные затраты.
5. Выведение функции затрат длительного периода. Кривая средних затрат длительного периода и отдача от масштаба.
6. Функции предложения конкурентной фирмы в коротком и длительном периодах. Методика выведения указанных функций из функций затрат.
7. Кривая отраслевого предложения. Излишек производителя. Эластичность предложения по цене.
8. Количественный подход к анализу полезности и спроса. Законы Госсена. Равновесие потребителя. Выведение функции индивидуального спроса.
9. Порядковый подход к анализу полезности и спроса. Равновесие потребителя. Выведение функции индивидуального спроса.
10. Кривые «доход – потребление» и «цена – потребление». Кривая Энгеля. Эластичность спроса по доходу.
11. Разложение общего изменения объема спроса при изменении цены на эффект замены и эффект дохода: сущность, значение, графическое изображение.
12. Построение кривой рыночного спроса. Излишек потребителя. Эластичность спроса по цене.
13. Отраслевое равновесие: понятие и виды. Устойчивость и неустойчивость рыночного равновесия.
14. Функции спроса и предложения: понятие, сущность, факторы их определяющие. Цена равновесия. Равновесие по Вальрасу и Маршаллу.
15. Паутинообразная модель: понятие, сущность, виды.
16. Регулирование рынка совершенной конкуренции: последствия введения акцизов, дотаций и установления директивных цен.
17. Условия максимизации прибыли при совершенной и несовершенной конкуренции.
18. Совершенная конкуренция. Равновесие конкурентного предприятия в коротком и длительном периодах.
19. Монополия. Равновесие фирмы в условиях монополии. Ущерб, причиненный монополией.
20. Последствия введения акцизов, дотаций и директивных цен на монополизированном рынке.
21. Ценовая дискриминация: сущность, условия осуществления, виды, значение для производителя и потребителя.
22. Естественная монополия: сущность, причины возникновения, методические основы регулирования цен.
23. Равновесие предприятия на рынке монополистической конкуренции. Влияние рекламы на состояние равновесия.
24. Олигополия: понятие и сущность. Олигополистические ценовые войны. Жесткость цен в условиях олигополии.
25. Картель: понятие, сущность, равновесие картеля и отдельной фирмы. Модель «ценообразования за лидером».
Задание для группы 417621
1. Предложение факторов производства. Построение функций предложения труда и предложения капитала.
2. Спрос на факторы производства. Построение индивидуальной и рыночной функции спроса на труд.
3. Статус фирмы на рынке факторов и условие максимизации прибыли. Сравнительный анализ состояния равновесия на рынке труда при совершенной конкуренции, монополии и монопсонии.
4. Двухсторонняя монополия на рынке труда. Минимум заработной платы и последствия его введения.
5. Общее и частичное равновесие: понятие, сущность, цена. Модель Вальраса.
6. Общее экономическое равновесия и общественное благосостояние, Экономическая эффективность и социальная справедливость.
7. Оптимальность по Парето: понятие, сущность, виды и методы определения.
8. Первая теорема общественного благосостояния: сущность и доказательство.
9. Общественные блага: понятие, сущность и виды. Определение оптимального объема производства общественных благ.
10. Внешние эффекты и внешние затраты: понятие, сущность, методы интернализации. Теорема Коуза.
11. Роль цен в распределении экономических ресурсов.
12. Позитивный и нормативный анализ в экономике.
13. Товар и его свойства. Современные тенденции в товарном мире.
14. Практическое применение теории потребительского выбора.
15. Влияние дохода и цен на оптимальный выбор потребителя.
16. Эффект дохода и эффект замещения в поведении потребителя.
17. Выигрыш (экономическая рента) предприятия. Влияние на ее величину изменения цены на товар предприятия.
18. Использование суммы выигрыша производителей и потребителей для оценки выгод и потерь от реализации государственной экономической политики.
19. Влияние совершенствования технологии производства продукции на экономические параметры конкурентного рынка.
20. Монополия как экономическое явление. Особенности монополизации белорусской экономики.
21. Монополия и экономическая власть. Механизм экономического господства монополии
22. Монополия и конкуренция. Формирование конкурентной среды в Республике Беларусь.
23. Монополистическая конкуренция и эффективность производства.
24. Роль дифференциации продукта на рынке монополистической конкуренции.
25. Реклама и стимулирование сбыта – факторы завоевания конкурентного преимущества
Задание для группы 417611
1. Проблемы формирования олигополистического рынка в Республике Беларусь.
2. Использование теории игр при моделировании стратегического взаимодействия фирм в условиях олигополии.
3. Типология моделей олигополии.
4. Антимонопольное регулирование экономики в Республике Беларусь.
5. Влияние развития профсоюзного движения на предложение и производительность труда.
6. Поведение предприятий на монопсонном рынке труда (на примере белорусских предприятий)
7. Зависимость между уровнем конкуренции на рынке продукции и величиной оплаты труда работников и специалистов.
8. Зависимость уровня заработной платы высококвалифицированных работников от степени конкуренции на рынке труда (на примере специалистов в области экономики и управления)
9. Формирование и функционирование рынка капитала в Республике Беларусь.
10. Предпринимательство как фактор производства и экономическая прибыль как факторный доход
11. Рынок ценных бумаг: сущность, структура, механизм функционирования.
12. Неопределенность и риск как источники экономической прибыли.
13. Земельные отношения в Республике Беларусь.
14. 2. Формирование экономических условий развития агробизнеса в нашей республике
15. Цена земли: факторы, динамика, тенденции.
16. Применение анализа общего равновесия к монопольным рынкам.
17. Понятие «Х-эффективности» Харви Лейбенштейна.
18. Чистый выигрыш и перераспределительные эффекты при свободной международной торговле.
19. Концепция оптимального загрязнения и его критика.
20. Меры государственного регулирования внешних эффектов.
21. Экологическая политика и теория внешних эффектов.
22. Учет риска и неопределенности при принятии решений руководителями предприятий.
23. Феномен «поражения победителя» на аукционных торгах.
24. Существующий мировой опыт решения проблемы «безбилетников» («зайцев»).
25. Последствия свободного доступа к благам, находящимся в общественной собственности.
26. Демократическая процедура голосования при представительной демократии с точки зрения теории общественного выбора.
27. Модель усредненного избирателя в теории общественного выбора
Задачи для выполнения контрольной работы по курсу «Микроэкономика»
Задание для группы 417511
Задача 1
При выпуске Q0 единиц продукции предельная производительность труда сравнялась со средней его производительностью.
1. Какова эластичность выпуска по труду при таком объеме выпуска?
Коэффициент эластичности выпуска будет:
2. Как будет изменяться средняя производительность капитала по мере дальнейшего увеличения выпуска за счет использования дополнительного труда? Будет:
1 - уменьшаться;
2 - увеличиваться;
3 - не изменится.
Правильный вариант:
Задача 2
Заполните пропуски в приведенной таблице, отображающей изменение технической результативности производства при фиксированном объеме капитала и увеличивающемся объеме используемого труда.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
L TP MPL APL
3 - - 30
4 - 20 -
5 130 - -
6 - 5 -
7 - - 20
Задача 3
Фирма работает по технологии, отображаемой производственной функцией Q = L0,6K0,4. Цена труда - 8 ден. ед., а цена капитала - 16 ден. ед.
Определить среднюю производительность труда при нахождении фирмы в состоянии равновесия.
APL = .
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до тысячых долей (три знака после разделительной точки)!
Задача 4
Фирма, работающая по технологии Q = L0,5K0,25, может затратить на покупку факторов производства 600 ден. ед. цена труда rL = 4, цена капитала rK = 1.
1. При каких объемах труда и капитала объем выпуска фирмы будет максимальным?
При L = и K =
2. Как изменится капиталовооруженность труда, если:
а) - бюджет фирмы возрастет в 1,5 раза;
1 - увеличится;
2 - уменьшится;
3 - не изменится.
Правильный вариант:
б) - цена труда возрастет в 1,5 раза.
1 - увеличится в 1,5 раза;
2 - уменьшится в 1,5 раза;
3 - не изменится.
Правильный вариант:
Задача 5
Продукция производится по технологии, отображаемой функцией Q = L0,25K0,5. Цены факторов производства равны: rL = 1; rK = 3.
Определить минимум средних затрат короткого периода при использовании следующих объемов капитала:
При К = 10, AC = ; К = 15, AC = ; К = 20, AC = .
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 6
При производстве 5 тыс. стульев предельные затраты сравнялись со средними переменными затратами.
Как будут изменяться совокупные средние затраты по мере увеличения выпуска?
1 - будут постоянно повышаться;
2 - будут постоянно снижаться;
3 - будут сначала снижаться, а потом повышаться;
4 - будут сначала повышаться, а потом снижаться.
Правильный вариант:
Задача 7
Опрос показал, что готовность жильцов трех домов платить за озеленение их двора выражается следующими функциями: P1 = 80 – Q; P2 = 60 – Q; P3 = 40 – Q,
где Pi – максимальная сумма денег, которую согласны заплатить жильцы i-го дома за очередное дерево.
Общие затраты на озеленение определяются по формуле
TC = 2Q + 0,5Q2.
1. Определить Парето-эффективное число деревьев во дворе дома.
Q =
2. Сколько деревьев будет посажено, если фирма, проводящая озеленение, установит цену за каждое дерево на уровне:
а) предельных затрат Парето-эффективного числа деревьев.
Q =
б) средних затрат Парето-эффективного числа деревьев.
Q =
Задача 8
При цене моркови 8 ден. ед. за 1 кг на рынке было три продавца со следующими показателями эластичности предложения по цене: eS1 = 1,6; eS2 = 2; eS3 = 1. Первый из них предлагал 10 кг, второй - 12 кг, а третий - 40 кг.
Определить объем рыночного отраслевого предложения при P = 12.
Объем отраслевого предложения будет:
Задача 9
Продукция на рынке продается тремя производителями; функции предложения каждого были следующими: 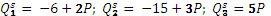
Определить отраслевую эластичность предложения по цене, когда цена на рынке будет равна 4,5 ден. ед.?
Отраслевая эластичность предложения по цене будет:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до тысячых долей (три знака после разделительной точки)!
Задача 10
Фирма имеет капитал К = 256 и технологию, отображаемую функцией  . Факторы производства она покупает по неизменным ценам: rL = 2; rK = 8 и продает свою продукцию на рынке совершенной конкуренции по цене Р = 432.
. Факторы производства она покупает по неизменным ценам: rL = 2; rK = 8 и продает свою продукцию на рынке совершенной конкуренции по цене Р = 432.
Каков будет объем прибыли в каждом из периодов?
Величина прибыли в коротком периоде: ; в длинном периоде:
Задача 11
Общие затраты конкурентной фирмы TC = 16 + 4Q2.
При какой цене фирма будет производить продукцию с минимальными средними затратами?
P = .
Задача 12
Производственная функция фирмы  . Она покупает труд по цене rL = 2.
. Она покупает труд по цене rL = 2.
Какую прибыль получит фирма при Р = 60?
Фирма получит прибыль:
Задача 13
Фирма работает по технологии Q = L0,25K0,5 и может покупать факторы производства по ценам rL = 2; rK = 10.
Сколько капитала она будет использовать, если сможет продавать свою продукцию по цене Р = 60?
Фирма будет использовать капитала.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Задача 14
Максим составил для себя следующую таблицу полезности трех благ. Имея 25.2 ден. ед., он купил 3 кг хлеба по цене 2 руб. за 1 кг, 4 л молока по цене 2,8 руб. за 1 л и 2 кг сахара по цене 4 руб. за 1 кг.
Номер порции Вид блага, ютила
Хлеб Молоко Яблоки ...
I 15 12 10 ...
II 10 11 8 ...
III 8 10 6 ...
IV 7 7 3 ...
V 5 6 1 ...
... ... ... ... ...
1. Следовал ли Максим второму закону Госсена?
1 - «Да». 2 - «Нет».
Правильный вариант:
2. Какой набор благ обеспечивает Максиму максимум полезности при его бюджете?
Максимум полезности обеспечит набор: кг хлеба, л молока и кг сахара.
Задача 15
Функция полезности Ивана имеет следующий вид: 
, где QA, QB, QC - объемы потребляемых благ А, В, С; бюджет Ивана равен 120 ден. ед.
Как изменится объем спроса Ивана на блага А и С, если цена блага В будет снижаться?
1 - повысится;
2 - понизится;
3 - не изменится.
Правильный вариант номер:
Задача 16
Функция полезности Николая имеет следующий вид:  , где QA, QB, QC - объемы потребляемых благ А, В, С; бюджет Николая равен 120 ден. ед.
, где QA, QB, QC - объемы потребляемых благ А, В, С; бюджет Николая равен 120 ден. ед.
1. Как изменится объем спроса Николая на блага А и С, если цена блага В будет снижаться?
1 - будет возрастать;
2 - будет понижаться;
3 - не изменится.
Правильный вариант номер:
2. Какой экономический смысл имеют вычитаемые числа в скобках функции полезности Николая?
1 - показывают, на сколько процентов возрастет общая полезность при увеличении объема соответствующего блага на один процент;
2 - представляют минимальные объемы потребления каждого блага независимо от их цен;
3 - представляют предельную полезность соответствующего блага.
Правильный вариант номер:
Задача 17
Известна функция полезности Никиты: U = QAQB; его бюджет - 36 ден. ед. Из всего множества доступных Никите при сложившихся ценах наборов благ известны два: QA = 6; QB = 2 и QA = 3; QB = 4.
Как Никита должен использовать свой бюджет, чтобы получить максимум полезности?
QA* = ; QB* =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . )
Задача 18
На рынке свинины имеется 50 бедных покупателей с бюджетом 80 денежных единиц у каждого и 25 зажиточных покупателей, у каждого из которых бюджет равен 120 денежных единиц. Предпочтения свинины говядине у всех покупателей одинаковые и характеризуются функцией полезности U = (Qc - 5)0,6·(Qg - 2)0,4, где Qc - количество свинины в килограммах; Qg - количество говядины в килограммах. Свинина производится по технологии  ; производят ее 144 конкурентных фирм, которые могут покупать труд и капитал в любом количестве по фиксированным ценам rL = 16, rK = 2.
; производят ее 144 конкурентных фирм, которые могут покупать труд и капитал в любом количестве по фиксированным ценам rL = 16, rK = 2.
Какова будет конъюнктура на рынке свинины при цене Р = 24?
1 - равновесие;
2 - дефицит;
3 - избыток.
Правильный вариант:
Задача 19
Сергей имеет 6 ед. блага А и 8 ед. блага В. Его функция полезности имеет вид U = (QA - 2)·(QB - 4).
1. За сколько единиц блага А Сергей согласится отдать 2 ед. блага В?
За: единиц блага А
2. Определить MRSAB Сергея до и после предложенного ему обмена благами (не забывайте, что eD < 0).
До обмена: . После обмена:
Задача 20
При ценах РА = 4; РB = 2 линия "доход - потребление" Константина имеет следующий алгебраический вид:
QA = 2QB - 5.
Определите, при каком бюджете Константин будет потреблять 6 единиц блага А.
При бюджете:
Задача 21
Бюджет Максима, равный 21 ден. ед., предназначен для покупки двух благ (А и В).
Его предпочтения относительно этих благ выражаются функцией
полезности  .
.
При ценах РА = 9; РB = 1 Максим купил 2 ед. блага А и 3 ед. блага В.
1. Оптимально ли Максим израсходовал бюджет?
1 - «Да»; 2 - «Нет». Правильный вариант:
2. Какой ассортимент благ обеспечит Максиму максимум полезности, если его бюджет снизится до 13,5 ден. ед.?
QA = ; QB =
3. Как изменятся объемы покупок Максима, если при исходном бюджете цена блага В снизится до 9/16 ден. ед.?
QA = ; QB = (введите числа с точностью до сотых долей (два знака после разделительной точки))!
4. На основе проведенного наблюдения за поведением потребителя дать характеристику благам, поставив:
0 (нет) и 1 (да) в нужные клетки приведенной ниже таблицы.
| Благо Взаимозаменяемое Взаимо дополняемое Нормальное «Некачественное» «Благо Гиффена» |
| А |
| B |
Задача 22
Функция полезности Ильи имеет вид U = (QA - 4)·(QB - 6), его бюджет M = 64, а цены благ PA = 1, PB = 1,5.
1. Определить перекрестную эластичность спроса на благо B в момент равновесия потребителя.
Перекрестная эластичность спроса на благо B в момент равновесия потребителя:
2. Выведите уравнение кривой безразличия, на которой находится потребитель в момент равновесия, и, используя его, определите, сколько единиц блага А будет потреблять Илья, если у него будет 150,5 ед. блага В?
Илья будет потреблять: единиц блага А.
3. Разложить реакцию индивида на эффекты замены и дохода, если цена блага B повысилась до 2 ден. ед.
Эффект замены: QB = ; QA =
Эффект дохода: QB = ; QA =
4. Определить разность между компенсирующим и эквивалентным изменениями дохода.
Разность между компенсирующим и эквивалентным изменениями дохода будет:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 23
Вадим покупает только три вида товаров: хлеб, колбасу и молоко. На хлеб он тратит 20%, на колбасу - 50% и на молоко - 30% своего дохода.
Определить эластичность спроса Вадима на молоко по доходу, если известно, что его эластичность спроса по доходу на хлеб равна -1, а на колбасу: +2.
Эластичность спроса на молоко по доходу будет в %:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 24
При цене 1 кг яблок 18 ден. ед. на рынке было три покупателя: их функции спроса по цене были прямолинейными. Первый купил 20 кг при эластичности спроса по цене -2; второй - 16 кг при -1,5 и третий - 24 кг при -2,5.
Определите эластичность рыночного спроса по цене.
Эластичность рыночного спроса по цене будет:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 25
Готовность абитуриентов платить за учебу в вузах выражается функцией P = 50 – 0,5N, где Р – сумма платы; N – число абитуриентов, тыс. чел. Выраженная в деньгах предельная общественная полезность высшего образования отображается функцией MU = 70 – 0,5N, где MU – предельная общественная полезность. Общие затраты вузов на подготовку специалистов заданы функцией TC = 10N + N2.
1. Определить величину внешнего эффекта подготовки специалиста с высшим образованием.
Величина внешнего эффекта:
2. Какое число студентов соответствует максимуму их суммарной полезности.
N =
3. Какое число студентов соответствует максимуму общественной полезности.
N =
4. Определить величину платы за обучение одного студента и сумму дотации на его обучение, соответствующие максимуму общественной полезности высшего образования.
Плата за обучение , сумма дотации
Задание для группы 417621
Задача 1
Благо В производят 50 фирм с одинаковой технологией, отображаемой функцией ;
факторы производства продаются по неизменным ценам rL = 2; rK = 8.
Продукцию покупают 100 потребителей со следующей функцией полезности:
 .
.
У всех покупателей одинаковый бюджет М = 120. Известны цены благ А и С: РА = 5; РC = 10.
Какую величину прибыли в этих условиях получает каждая фирма?
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до тысячных долей (три знака после разделительной точки)!
Задача 2
Результаты наблюдения за поведением потребителя на рынке представлены в таблице.
| Наблюдение | M | PA | PB | QA | QB |
| I | 10,4 | ||||
| II | |||||
| III | 6,5 |
1. Можно ли по этим результатом признать потребителя максимизирующим, если его предпочтения в момент наблюдения не менялись?
1 -«Да». 2 - «Нет». Правильный ответ номер:
2. Ответить на этот же вопрос при условии, что при наблюдении II индивид купил по 9 ед. обоих благ.
1 -«Да». 2 - «Нет». Правильный ответ номер:
Задача 3
На рынке есть три покупателя со следующими функциями спроса:

, где Мi - доход i -го покупателя.
На сколько возрастет отраслевой спрос при снижении цены с 20 до 10:
а) когда все покупатели имеют одинаковый доход по 50 ден. ед.;
б) когда в пределах той же общей суммы доходы покупателей дифференцированы следующим образом: M1 = 20; M2 = 50; M3 = 80.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 4
Функция затрат целлюлозной фабрики  . Свою продукцию она продает по неизменной цене Р1 = 40. Затраты рыболовецкого кооператива, использующего тот же водоем, что и фабрика, растут по мере увеличения своего выпуска и выпуска фабрики:
. Свою продукцию она продает по неизменной цене Р1 = 40. Затраты рыболовецкого кооператива, использующего тот же водоем, что и фабрика, растут по мере увеличения своего выпуска и выпуска фабрики: 
Свою продукцию кооператив продает по неизменной цене Р2 = 80. Оба предприятия стремятся к максимуму прибыли.
1. Определить объемы выпуска и прибыли каждого предприятия, если водоем является бесплатным общественным благом.
Q1 = , Q2 = , 1 = , 2 =
2. Рыболовецкий кооператив имеет право взимать с целлюлозной фабрики фиксированную плату за каждую единицу ее выпуска. Какая плата будет установлена?
Z =
3. Целлюлозная фабрика имеет право на загрязнение водоема в следствие выпуска своей продукции. Какую фиксированную плату кооператив пожелает предложить фабрике за каждую единицу сокращения ее выпуска и каковы будут объемы выпуска и прибыли каждого предприятия?
Z = , Q1 = , Q2 = , 1 = , 2 =
4. Фабрика и кооператив решили объединится. Определить объем выпуска и прибыль объединенного хозяйства.
Q1 = , Q2 = , =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Задача 5
На рынке яиц установилось равновесие при P = 4 и Q = 18. При этом коэффициент прямой эластичности спроса равнялся: -0,05, а коэффициент прямой эластичности предложения: +0,1.
1. Какова будет цена яиц, если спрос на них возрастет на 10%, а их предложение - на 5% при предположении, что в пределах указанных изменений спроса и предложения их графики прямолинейны?
P* = , Q* =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
2. Отобразить происшедшие изменения на графике.
Задача 6
Отраслевой спрос задан функцией QD = 12 - P, а технология производства данной продукции – функцией 
Ставка заработной платы равна 0,5 ден. ед.
1. Определить равновесные значения цены и выпуска.
P* = , Q* =
2. Вычислить разность между изменением суммы излишков производителей и потребителей и доходом государства при введении налога на каждую единицу проданной продукции в размере 1 ден. ед.
Чистые потери общества:
3. Определить разность между изменением суммы излишков производителей и потребителей и расходами государства при введении дотации за каждую единицу проданной продукции в размере 1 ден. ед.
Разность:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 7
Известны функции рыночного спроса: QD =10 - P и предложения: QS = -5 + 2P. За каждую проданную единицу продукции производитель должен платить налог в размере 1,5 ден. ед.
Какую часть этого налога производитель перекладывает на потребителя?
Производитель перекладывает на потребителя:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 8
Рынок сигарет представлен следующими функциями спроса и предложения: QD = 36 - 2P;QS = -4 + 3P.
1. Какую максимальную сумму налога можно собрать с этого рынка путем взимания акциза с каждой проданной пачки сигарет?
Максимальная сумма налога будет:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
2. Представить результат в виде кривой Лаффера.
Задача 9
Спрос на картофель в Эстонии задан функцией QЭD = 50 - 0,5PЭ, а в Псковской области - QПD = 120 - PП. Функция предложения картофеля по цене в Эстонии QЭS = PЭ - 10, а в Псковской области - QПS = PП - 20.
1. Определить как изменятся излишки производителей и потребителей в каждом из регионов в результате создания общего рынка картофеля при отсутствии транспортных расходов.
В результате объединения рынков в Эстонии сумма излишков возросла на:
В результате объединения рынков в Псковской области сумма излишков возросла на:
2. То же, что в задании «1», если перевозка единицы картофеля из одного региона в другой обходится в 10 денежных единиц.
В результате объединения рынков в Эстонии сумма излишков возросла на:
В результате объединения рынков в Псковской области сумма излишков возросла на:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 10
Функция спроса на розы имеет вид QtD = 200 - Pt, а функция их предложения QtS = 0,5Pt-1 - 10, где t - дни недели от понедельника до субботы.
1. Определить равновесную цену роз.
P* = , Q* =
2. Какие цены на розы будут по дням недели, если в воскресенье на рынке была равновесная цена, а в понедельник спрос возрос таким образом, что при каждом значении цены покупали на 30 роз больше?
Понедельник: P1 = . Вторник: P2 = . Среда: P3 =
Четверг: P4 = . Пятница: P5 = . Суббота: P6 =
3. Какова равновесная цена после увеличения спроса?
P* = , Q* =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 11
Функция спроса на гвоздики имеет вид QtD = 200 - 0,5Pt, а функция их предложения - QtS = 0,7Pt-1 - 10, где t - дни недели от понедельника до субботы.
1. Определить равновесную цену гвоздики.
P* = , Q* =
2. Какие цены на гвоздики будут по дням недели, если в воскресенье на рынке была равновесная цена, а в понедельник спрос возрос таким образом, что при каждом значении цены покупали на 30 гвоздик больше?
Понедельник: P1 = . Вторник: P2 = . Среда: P3 =
Четверг: P4 = . Пятница: P5 = . Суббота: P6 =
3. Какова равновесная цена после увеличения спроса?
P* = , Q* =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 12
На рынке c прямолинейными функциями спроса и предложения установилось равновесие P* = 36; Q* = 120; при этом eD = - 0,75 и eS = 1,5.
1. Определить величину дефицита, если правительство установит верхний предел цены на уровне 30 ден. ед.
Величина дефицита будет:
2. Какова будет цена на «черном» рынке, если известно, что каждая единица продукции, продаваемая на нем, обходится продавцу на 2 ден. ед. дороже.
Цена на «черном» рынке будет:
3. Представьте результаты решения графически.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 13
Отраслевой спрос на продукцию характеризуется функцией QD = 120 - 3P. Функция общих затрат фирмы, производящей данную продукцию, имеет вид TC = 10 + 8Q - 4Q2 + Q3.
1. По какой цене и сколько единиц продукции будет продано, если в отрасли работают 20 таких фирм?
P* = , Q* =
2. Сколько таких фирм останется в отрасли в условиях совершенной конкуренции в длинном периоде?
Таких фирм останется в отрасли:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 14
В отрасли работают 10 фирм, общие затраты которых характеризуются функцией TC10 = 10 + 8q - 4q2 + q3, и 8 фирм с функцией TC8 = 15 + 20q - 5q2 + 0,5q3. Отраслевой спрос представляет функция QD = 150 - 2P.
Определить цену равновесия и объем отраслевой реализации в коротком и длинном периодах.
Короткий период: P = ; Q =
Длинный период: P = ; Q =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 15
В отрасли работают 5 фирм со следующими функциями затрат: TC1 = 4 + Q-1; TC2 = 1 + 2Q2; TC3 = 12 + 3Q3; TC4 = 4 + 4Q4; TC5 = 2 + 5Q5. В коротком периоде каждая из фирм не может выпускать больше 4 ед. продукции. Отраслевой спрос отображается линейной функцией. В отрасли установилось краткосрочное равновесие, при котором производственные мощности всех фирм используются полностью, но предельная фирма возмещает только переменные затраты. Коэффициент эластичности спроса по цене равен - 1.
Как должна сместиться прямая спроса, чтобы при той же его эластичности и полном использовании имеющихся производственных мощностей установилось долгосрочное равновесие?
1 - сдвинуться вправо при том же наклоне к оси абсцисс;
2 - сдвинуться влево при том же наклоне к оси абсцисс;
3 - увеличить угол наклона к оси абсцисс;
4 - уменьшить угол наклона к оси абсцисс.
Правильный вариант:
Задача 16
Прямая линия отраслевого спроса пересекает ось цены в значении 10. При выпуске, соответствующем точке Курно, предельные затраты монополии равны 4.
Определите цену максимизирующую прибыль монополии.
Цена максимизирующую прибыль монополии будет:
Задача 17
Спрос на продукцию монополии, максимизирующей прибыль, отображается функцией QD = 13 - P/3.
Фирма установила P = 20.
Каковы предельные затраты фирмы?
MC =
Задача 18
Функция спроса на монополизированном рынке имеет вид QD = 301 - P; функция общих затрат монополии - TC = 120 + Q + Q2; капиталоемкость производства характеризуется формулой K = 500Q.
По какой цене будет продаваться продукция при стремлении монополии к максимуму:
а) прибыли, б) выручки, в) нормы прибыли?
а) Прибыль монополии достигает максимума при: P* =
б) Выручка монополии достигает максимума при: P* =
в) Норма прибыли монополии достигает максимума при: P* =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 19
Задан отраслевой спрос на благо P = g - hQ. Его продает одна фирма, стремящаяся к максимуму прибыли. Затраты на производство представлены функцией общих затрат TC = m + nQ.
Какие параметры функции спроса и функции общих затрат монополии влияют на величину коэффициента эластичности спроса по цене в состоянии отраслевого равновесия?
Предлагаемый ответ: (влияет - «1»; не влияет - «0»):
g = ; h = ; m = ; n = .
Задача 20
В отрасли работают 10 фирм с одинаковыми функциями затрат TCi = 4 + 2qi + 0,5q2i. Отраслевой спрос задан функцией: QD = 52 - 2P. Собственник одной из фирм предложил своим конкурентам передать ему свои предприятия, обещая за это выплачивать им регулярный доход, в 2 раза превышающий получаемую ими прибыль.
1. Насколько возрастет прибыль инициатора монополизации отрасли, если его предложение будет принято?
Прибыль возрастет в: раз.
2. Насколько сократятся излишки потребителей?
Излишки потребителей сократятся на: денежных единиц.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 21
На монополизированном рынке спрос представлен функцией QD = 84 - P, а функция общих затрат монополии имеет вид TC = Q2.
Определить максимальную прибыль монополии при продаже всего выпуска по единой цене и осуществлении ценовой дискриминации первой степени.
Максимальная прибыль при продаже по единой цене составит: , а при ценовой дискриминации первой степени:
Задача 22
При линейной функции спроса монополия получает максимум прибыли, реализуя 10 ед. продукции по цене 24 ден. ед. Функция общих затрат монополии TC = 100 + 4Q + 0,25Q2.
1. Как изменится цена блага, если с каждой проданной его единицы будет взиматься налог в размере 7 ден. ед.?
Цена блага возросла на: ден. ед.
2. Как изменится прибыль монополии?
Прибыль монополии уменьшилась на: ден. ед.
3. Какова сумма получаемого налога?
Сумма налога будет: ден. ед.
4. Как изменятся излишки потребителей?
Излишки потребителей сократились на: ден. ед.
Задача 23
Издатель, стремящийся к максимуму прибыли, заключил с автором договор о том, что в качестве гонорара будет платить ему 10% выручки от продажи его книги. Функция спроса на книгу имеет вид QD = a - bP.
Захотят ли издатель и автор назначить одинаковую цену на книгу?
1: «Да», 2: «Нет».
Правильный вариант:
Задача 24
Монополия, максимизирующая прибыль, владеет двумя предприятиями, на которых может производиться один и тот же вид продукции с разными затратами: TC1 = 10q1; TC2 = 0,25q22. Спрос на продукцию характеризуется функцией QD = 200 - 2P.
Сколько и на каком предприятии монополия будет производить продукции?
На первом предпрятии будет производиться: ед. продукции;
На втором предпрятии будет производиться: ед. продукции.
Задача 25
Фирма, имеющая функцию общих затрат TC = 5 + 4Q + 0,25Q2, установила, что функция спроса на ее продукцию имеет вид

При каком объеме выпуска фирма получает максимум прибыли?
Максимум прибыли обеспечит объем выпуска:
Задание для группы 417611
Задача 1
Монополия может продавать продукцию на двух сегментах рынка с различной эластичностью спроса: Q1D = 160 – P1; Q2D = 160 – 2P2. Ее функция общих затрат имеет вид TC = 5 + 5Q + 0,25Q2.
1. При каких ценах на каждом из сегментов монополия получит максимум прибыли?
При: P1 = и P2 = .
2. Сколько ед. продукции будет продаваться на каждом сегменте рынка при запрете ценовой дискриминации?
Q1 = ; q2 = .
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 2
Функция спроса на продукцию фирмы, максимизирующей прибыль, имеет вид QD = 33,5 – 0,5P, а функция затрат отображается формулой TC = 2 + 4Q – Q2 + Q3/3.
Определите цену и объем продаж:
а) в заданных условиях:
P = , Q =
б) при введении налога с единицы выпуска в размере 15 ден. Ед.:
P = , Q =
в) при введении 10%-го налога с прибыли:
P = , Q =
г) при введении 20%-го налога с выручки:
P = , Q =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 3
Известны функция спроса на продукцию монополистического конкурента QA = 30 – 5PA + 2PB и функция его общих затрат TCA = 24 + 3QA.
Определить PA и PB после установления отраслевого равновесия в длинном периоде.
PA = ; PB =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 4
Известны функции спроса на два вида минеральных вод Q1D = 10 – 2P1 + P2; Q2D = 12 – P2 + P1. Минеральная вода поступает из природных фонтанов, поэтому TC1 = TC2 = 0.
- Сколько и по какой цене будет продано каждого вида минеральной воды, если владельцы фонтанов стремятся к максимуму прибыли.
P1: Q1:
P2: Q2:
2. Выведите функции спроса на каждый вид воды в состоянии равновесия и по ним определите объемы спроса на каждый вид воды при Р1 = Р2 = 1.
Q1 = , Q2 =
3. Определите границы смещения кривой спроса на каждый вид воды и вычислите по их формулам максимальные и минимальные объемы спроса при Р1 = Р2 = 1.
Q1,min = , Q1,max = , Q2,min = , Q2,max =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Задача 5
На рынке дуополии отраслевой спрос представлен функцией P = 50 – 0,25Q; известны функции общих затрат обоих производителей продукции TCA = 10 + 0,15Q2A; TCB = 25 + 10QB.
1. Определить цену равновесия и объем предложения каждого из дуополистов, если они ведут себя в соответствии с предпосылками: а) модели дуополии Курно; б) модели дуополии Штакельберга при лидерстве фирмы А; в) модели дуополии Штакельберга при лидерстве фирмы В; г) модели картеля.
А) – модель дуополии Курно:
P = Q = A = B =
б) – модели дуополии Штакельберга при лидерстве фирмы А:
P = Q = A = B =
в) – модели дуополии Штакельберга при лидерстве фирмы B:
P = Q = A = B =
г) – модели картеля:
P = Q = A = B =
ПРИМЕЧАНИЕ. Введите числа с точностью до целых чисел!
Задача 6
Рыночный спрос на орехи отображается функцией QD = 195 – 2,5P. Орехи продают две фирмы А и В; известны их уравнения реакции на выпуск своего конкурента:
qA = 60 – 0,4qB;
qB = 80 – 0,5qA.
По какой цене будут продаваться орехи?
P =
Задача 7
В отрасли функционируют 80 мелких фирм с одинаковыми функциями затрат Tci = 2 + 8qi2, и еще одна крупная фирма, выступающая в роли лидера, с функцией затрат TCл = 20 + 0,275qл2. Отраслевой спрос представлен функцией QD = 256 – 3P.
Какая цена сложится на рынке и как он будет поделен между лидером и аутсайдерами?
P =
Лидер удовлетворит % спроса. Аутсайдеры - % спроса
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 8
В отрасли работает одна крупная фирма лидер и группа аутсайдеров. Суммарное предложение аутсайдеров отображается функцией: QAS = - 1 + 2P; при цене Р = 13 аутсайдеры полностью удовлетворяют отраслевой спрос без лидера. В отрасли установилось равновесие при P = 10; Q = 28.
Выведите функцию отраслевого спроса и функцию спроса на продукцию лидера и по ним рассчитайте общий объем продаж и объем продаж лидера при Р = 10.
Общий объем продаж составит: , объем продаж лидера:
Задача 9
Функция полезности Олега имеет вид U·(M + 9)0,5·F0,25, где М – сумма денег, представляющая все потребительские блага, F – свободное время. За вычетом времени сна индивид располагает 16,5 ч времени в сутки.
Поэтому F = 16,5 – L, а М = rLL.
1. Сколько часов Олег будет работать в течение суток при цене труда: а) rL = 1, б) rL = 3?
a) LS = , б) LS =
2. Разложить реакцию Олега на повышение цены труда на эффекты замены и дохода?
Эффект замены: сокращение свободного времени на час.
Эффект дохода: увеличение свободного времени на час.
3. Какую сумму налога будет платить Олег, если при ставке зарплаты rL = 3 подоходный налог составляет 33,33%?
Сумма налога:
4. Какая величина подушного (паушального) налога снижает благосостояние Олега на столько же, на сколько его уменьшил подоходный налог?
Величина подушного налога:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . )
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 10
Предпочтения Михаила относительно нынешних (С0) и будущих (С1) благ отображаются двухпериодной функцией полезности U = CD0,6·C10,4. Его доход в текущем периоде y0 = 120, а в будущем y1 = 150.
1. Определить объемы его сбережений в текущем периоде и объемы потребления в обоих периодах при ставках процента
i = 20; 50; 87,5; 95%.
| I | C0 | S0 | C1 |
| 0,2 | |||
| 0,5 | |||
| 0,875 | |||
| 0,95 |
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . )
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
2. Доволен ли Михаил повышением ставки процента?
1. «Доволен»; 2. «Не доволен».
Правильный вариант ответа:
Задача 11
Экономика состоит из двух потребителей (I,II) и двух фирм (A, B), производящих по одному виду продукции. Предпочтения потребителей представлены их функциями полезности 
где Qj,i – количество j-го блага, потребляемого i-м индивидом.
Бюджеты потребителей формируются за счет продажи фирмам имеющихся объемов труда и капитала: 
Кроме того, при наличии у фирм прибыли она полностью распределяется между собственниками капитала, т.е. потребитель I получает 60%, а потребитель II – 40% прибыли. Фирмы работают по технологиям, представленным следующими производственными функциями: 
Потребители и фирмы при определении своего поведения на рынках воспринимают цены как экзогенные параметры.
Определить вектор относительных цен, обеспечивающих общее экономическое равновесие при rL = 1; доходы каждого потребителя и объемы потребляемых ими благ.
PA = ; PB = ; rK = ; MI ; MII =
QAI = ; QAII = ; QBI = ; QBII =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до тысячых долей (три знака после разделительной точки)!
Задача 12
Кривая рыночного спроса на труд отображается функцией LD = 92 – 2rL, а кривая рыночного предложения труда – функцией LS = - 10 + rL.
Какой максимальной цены труда могут добиться рабочие, образовав профсоюз?
rL,max =
Задача 13
В отрасли предложение труда поступает от 100 рабочих с одинаковыми функциями полезности
U = (M + 9)0,5·(16,5 – L)0,25, где М – сумма денег, представляющая все потребительские блага, L – количество часов труда. Спрос на труд предъявляют 20 фирм производящих продукцию по технологии, отображаемой функцией Q = 4L0,5, и продающих ее по неизменной цене P = 6.
Какая цена труда сложится в отрасли и сколько часов будет работать каждый рабочий?
Цена труда будет:
Каждый рабочий будет работать: час.
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 14
Производственная функция фирмы Q = 4L0,5.
Определить объем спроса фирмы на труд, если она является:
а) совершенном конкурентом на рынке своего продукта при Р = 9 и рынке труда при rL = 6;
б) монополистом на рынке своего продукта, спрос на который представлен функцией QD = 24 – P, и рынке труда при rL = 6;
в) совершенном конкурентом на рынке своего продукта при Р = 9 и единственным покупателем труда, предложение которого представлен функцией LS = - 2 + rL;
г) монополистом на рынке своего продукта, спрос на который представлен функцией QD = 24 – P, и единственным покупателем труда, предложение которого представлено функцией LS = - 2 + rL.
А) L = ; б) L = ;
в) L = ; г) L = .
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 15
Спрос на продукцию фирмы, стремящейся максимизировать прибыль, отображается функцией QD = 240 – 2P, а технология производства – функцией Q = 2L0,5. Фирма является единственным покупателем труда, предложение которого представлено функцией LS = (rL/6)2.
Сколько труда фирма будет использовать при рыночном установлении цены труда и установлении ее минимума rL,min = 25?
При рыночной цене: LD = , при директивной: LD =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите число с точностью до сотых долей (два знака после разделительной точки)!
Задача 16
Хозяйство, ведущееся в условиях совершенной конкуренции, располагает 60 ед. труда и 10 ед. капитала. Технология производства продукции отображается производственной функцией Q = L0,75K0,25; цена труда rL = 1.
1. В какой пропорции ценность произведенной продукции распределится между трудом и капиталом?
Доля труда будет: %; доля капитала: %
2. Как изменится эта пропорция, если рабочие добьются повышения цены труда в 1,5 раза?
1. Увеличится в 1,5 раза.
2. Уменьшится в 1,5 раза.
3. Не изменится.
Правильный вариант:
Задача 17
Технология фирмы задана функцией  . Она закупает факторы производства по фиксированным ценам rK = 4; rL = 1. Спрос на продукцию фирмы представлен функцией QD = 40 – 2P.
. Она закупает факторы производства по фиксированным ценам rK = 4; rL = 1. Спрос на продукцию фирмы представлен функцией QD = 40 – 2P.
- Выведите функции спроса фирмы на факторы производства в длинном периоде и рассчитайте по ним объемы спроса на труд и капитал при rL = 9 и rK = 4.
LD = ; KD =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
2. Как созданная ценность блага распределится на доходы факторов производства и монопольную прибыль?
Монопольная прибыль будет:
Задача 18
Продается ветреная электростанция, которая в течение пяти ближайших лет обеспечит следующий поток чистых годовых доходов: 160, 150, 140, 130, 120 ден. Ед.
Какую максимальную цену стоит заплатить за электростанцию, если известно, что в эти пять лет депозитная ставка процента будет иметь следующую динамику, %: 5, 6, 4, 5, 7.
За электростанцию стоит заплатить:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 19
До момента гашения облигации с купонным доходом 12 ден. Ед. и номиналом (суммой гашения) 100 ден. Ед. остается 3 года.
Как изменится рыночная цена облигации, если рыночная ставка процента возрастет с 8 до 10%?
Рыночная цена облигации изменится на:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 20
В таблице представлены данные двух проектов заготовки древесины.
Проект
Годы
2000 2001 2002 2003 2004 2005
Подготовительные работы Заготовка Рекультивация
1 40 50 60 30 80 -
2 - 65 90 35 20 55
Подсчитать полные затраты на заготовку древесины по каждому проекту, если ставка процента i = 10%.
Затраты по 1 проекту: , по 2 проекту:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 21
В хозяйстве, состоящем из двух отраслей, спрос и предложение представлены следующими функциями:
. 
Возможно ли в этом хозяйстве общее экономическое равновесие, является ли оно устойчивым?
Общее экономическое равновесие достигается при: PA = , PB =
Оно является устойчивым: 1. «Да»; 2. «Нет».
Правильный вариант ответа:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 22
В хозяйстве, состоящем из двух отраслей, спрос и предложение представлены следующими функциями:

Возможно ли в этом хозяйстве общее экономическое равновесие, является ли оно устойчивым?
Общее экономическое равновесие достигается при: PA = , PB =
Оно является устойчивым: 1. «Да»; 2. «Нет».
Правильный вариант ответа:
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до десятых долей (один знак после разделительной точки)!
Задача 23
Выведите уравнение кривой производственных возможностей в коробке (диаграмме) Эджуорта.
1. Определите по нему, сколько капитала должно использоваться при производстве блага A с 10 ед. труда.
Должно использоваться капитала.
2. Представьте выпуск обоих благ в виде функции от тех значений LA, которые соответствуют оптимальности по Парето в производстве и, используя эти функции, найдите значения QA и QB при LA = 12:
QA = ; QB =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 24
Известны функции полезности двух потребителей: 
Каждый из них имеет по 20 ед. блага А и по 30 ед. блага В.
1. Является ли исходное распределение благ Парето-эффективным?
1. «Да»; 2. «Нет».
Правильный вариант ответа:
2. Какое из ниже приведенных распределений благ между индивидами обеспечивает улучшение по Парето?
1. QA,I = 25; QB,I = 23; QA,II = 15; QB,II = 37.
2. QA,I = 25; QB,I = 14; QA,II = 15; QB,II = 46.
Правильный вариант ответа:
3. Выведите уравнение контрактной линии в коробке (диаграмме) Эджуорта и определите по нему, сколько единиц блага А должен иметь потребитель I при наличии у него 20 единиц блага B в оптимальном по Парето распределении.
Потребитель I должен иметь: единиц блага А.
4. Какая конъюнктура сложится на каждом из рынков при ценах РА = 2, РB = 1?
Варианты ответов:
1. На рынке блага А дефицит, на рынке блага В избыток.
2. На рынке блага В дефицит, на рынке блага А избыток.
3. Равновесие на обоих рынках.
Правильный вариант ответа:
5. При каком соотношении цен установится общее равновесие?
РА = ; РB =
6. На сколько увеличится общая полезность каждого потребителя при ОЭР по сравнению с исходным состоянием?
UI = ; UII =
ПРИМЕЧАНИЕ. В качестве десятичного разделителя используйте точку ( . ).
Введите числа с точностью до сотых долей (два знака после разделительной точки)!
Задача 25
Два индивида имеют по 4 ед. блага А и по 5 ед. блага В.
Функция полезности 1-го индивида и 2-го индивида
