Infinitesimal and infinitely large functions.
Vocabulary
| 1. | 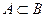 A is subset of B A is subset of B
| A- лю А – подмножество В |
| 2. |  any, for any any, for any
| любой, для любого |
| 3. |  exist exist
| существует |
| 4. | : such that | такой что |
| 5. |  x belongs to A x belongs to A
| х принадлежит А |
| 6. |  x tends to x0 x tends to x0
| х стремится к х0 |
| 7. | mathematical analysis | математический анализ |
| 8. | associate | ставить в соответствие |
| 9. | the domain of function | область определения функции |
| 10. | the range of function | множество значений функции |
| 11. | increasing | возрастающий |
| 12. | nondecreasing | неубывающий |
| 13. | decreasing | убывающий |
| 14. | nonincreasing | невозрастающая |
| 15. | enumerated | перечисленный |
| 16. | monotonous | монотонный |
| 17. | strictly monotonous | строго монотонный |
| 18. | symmetric | симметричный |
| 19. | mutually | взаимно |
| 20. | bounded (unbounded) | ограниченный (неограниченный) |
| 21. | output | результат |
| 21. | approximately | приблизительно |
| 22. | limit | предел |
| 23. | sufficiently | достаточно |
| 24. | imply | влечь, иметь следствием |
| 25. |  neighborhood neighborhood
|  окрестность окрестность
|
| 26. | quotient | частное |
| 27. | infinitesimal | бесконечно малый |
| 28. | infinitely large | бесконечно большой |
| 29. | comparison | сравнение |
| 30. | listed | перечисленные |
Section III. The basic concepts of mathematical analysis.
The concept of function.
Definition 1.1:A mathematical relation such that each element of a given set  (the domain of function) is associated with a unique element of another set
(the domain of function) is associated with a unique element of another set  ( the range of function) is called a function and denote
( the range of function) is called a function and denote  .
.  is called independent variable,
is called independent variable,  – dependent variable.
– dependent variable.
There are different methods of representation of functions, such that; tabular, analytical (be means of the formulas), graphical.
Definition 1.2:A set of points in the coordinate plane with coordinates  is called the graph of a function
is called the graph of a function  .
.
Definition 1.3:If  ,
,  and
and  , then:
, then:
1)  is increasing on
is increasing on  if
if  whenever
whenever  ;
;
2)  is nondecreasing on
is nondecreasing on  if,
if,  whenever
whenever  ;
;
3)  is decreasing on
is decreasing on  if
if  whenever
whenever  ;
;
4)  is nonincreasing on
is nonincreasing on  if
if  whenever
whenever  .
.
Functions listed in 1) – 4) are called monotonous; 1), 3) are called strictly monotonous.
Definition 1.4:For any  and
and  , if
, if  , then a function
, then a function  is called an even function, if
is called an even function, if  – an odd function.
– an odd function.
Definition 1.5:Inverse function is a function obtained by expressing the dependent variable of one function as independent variable of another; functions  and
and  are mutually inverse functions if
are mutually inverse functions if  and
and  .
.
Definition 1.6:Function  defined on some set
defined on some set  is called bounded on this set, if there is a positive number
is called bounded on this set, if there is a positive number  such that for any
such that for any  belonging to the set
belonging to the set  the inequality holds
the inequality holds  . Otherwise, the function is said to be unbounded.
. Otherwise, the function is said to be unbounded.
Limit of a function.
Definition 2.1:The number  is said to be the limit of the function
is said to be the limit of the function  as
as  , if for all values
, if for all values  , lying sufficiently close to
, lying sufficiently close to  , the corresponding values of the function
, the corresponding values of the function  are arbitrary close to the number
are arbitrary close to the number 
 .
.
Definition 2.2:The number  is called the limit of the function
is called the limit of the function  as
as  , if for any positive number
, if for any positive number  exists the positive number
exists the positive number  such, that for all
such, that for all  , different from
, different from  , and satisfying the inequality
, and satisfying the inequality  , implies the inequality
, implies the inequality  .
.
Algebra of limits.
The follow rules hold if  and
and  .
.
1. Sum rule:  ;
;
2. Difference rule:  ;
;
3. Product rule:  ;
;
4. Quotient rule:  , if
, if  .
.
Let to prove the first rule. To show that  we must show that
we must show that  , such that for all
, such that for all  satisfying inequality
satisfying inequality  implies
implies


From 



 From
From 


Let  . It means that
. It means that  and
and  hold for all
hold for all  such that
such that 
and we get
 .
.
Rule is proved.
Infinitesimal and infinitely large functions.
|
 is called an infinitesimal as
is called an infinitesimal as  , if
, if  This means that
This means that  (however small)
(however small)  such that for all
such that for all  satisfying inequality
satisfying inequality  , implies
, implies  .
.
Definition 4.2:The inverse of an infinitesimal, that is,  is an infinity large function. In this case we write
is an infinity large function. In this case we write  .
.
It is possible from limit rules for functions to draw the corresponding propositions for infinitesimal functions:
1. A sum of any finite number of infinitesimals is an infinitesimal
2. The product of a bounded function and an infinitesimal is an infinitesimal.
3. The product of any finite number of infinitesimals is an infinitesimal