Понятие функциональной и статистической зависимости.
Введение в эконометрическое моделирование.
Рассмотрим следующую ситуацию. Допустим, мы хотим продать автомобиль и решили дать объявление о продаже в газете. Естественно, перед нами встаёт вопрос: какую цену указать в объявлении?
Очевидно, мы будем руководствоваться информацией о цене, которую выставляют другие продавцы подобных автомобилей.. Что значит «подобные автомобили»? – Очевидно, это автомобили, обладающие близкими значениями таких факторов, как год выпуска, пробег, мощность двигателя. Проглядев колонку объявлений, мы формируем своё мнение о рынке интересующего нас товара и, возможно, после некоторого размышления, назначаем цену.
На этом простейшем примере, на самом деле можно проследить основные моменты эконометрического моделирования. Рассмотрим наши действия более формализовано.
Мы ставим задачу определить цену – величину, формируемую под воздействием некоторых факторов (года выпуска, пробега и т.д.). Такие зависимые величины обычно называются зависимыми (объясняемыми) переменными, а факторы, от которых они зависят, - объясняющими.
Формируя общее мнение о состоянии рынка, мы обращаемся к интересующему нас объекту и получаем ожидаемое значение зависимой переменной при заданных значениях объясняющих переменных.
Указанная конкретная цена – наблюдаемое значение зависимой переменной зависит также и от случайных явлений – таких, например, как характер продавца, его потребность в конкретной денежной сумме, возможные сроки продажи автомобиля и др.
Продавец-одиночка вряд ли будет строить какую-либо математическую модель, но менеджер крупного салона, специализирующегося на торговле автомобилями на вторичном рынке, скорее всего, захочет иметь более точное представление об ожидаемой цене и о возможном поведении случайной составляющей. Следующий шаг и есть эконометрическое моделирование.
Общим моментом для любой эконометрической модели является разбиение зависимой переменной на две части – объяснённую и случайную. Сформулируем задачу моделирования самым общим, неформальным образом: на основании экспериментальных данных определить объяснённую часть и, рассматривая случайную составляющую как случайную величину, получить (возможно, после некоторых предположений) оценки параметров её распределения.
Таким образом, эконометрическая модель имеет следующий вид::
Наблюдаемое Объяснённая часть, зави- Случайная со-
значение зави- сящая от значений объ- ставляющая
симой переменной ясняющих переменных
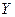 =
= 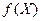 +
+ 
Остановимся теперь на целях моделирования. Предположим, получено следующее выражение для объяснённой части переменной 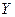 - цены автомобиля:
- цены автомобиля:

где  - ожидаемая цена автомобиля,
- ожидаемая цена автомобиля,  - срок эксплуатации автомобиля (в годах),
- срок эксплуатации автомобиля (в годах),  - пробег (в тыс. км).
- пробег (в тыс. км).
Каково практическое применение полученного результата? Во-первых, он позволяет понять: как именно формируется рассматриваемая экономическая переменная – цена на автомобиль. Во-вторых, он даёт возможность выявить влияние каждой из объясняющих переменных на цену автомобиля (так, в данном случае цена нового автомобиля (при  =0,
=0,  =0) 1800 у.е., при этом только за счет увеличения срока эксплуатации на 1 год цена автомобиля уменьшается в среднем на 1000 у.е., а только за счет увеличения пробега на 1 тыс. км – на 0,5 у.е.). В-третьих, что, пожалуй, наиболее важно, этот результат позволяет прогнозировать цену на автомобиль, если известны его основные параметры. Теперь менеджеру не составит большого труда определить ожидаемую цену вновь поступившего для продажи автомобиля, даже если его год выпуска и пробег не встречались ранее в данном салоне.
=0) 1800 у.е., при этом только за счет увеличения срока эксплуатации на 1 год цена автомобиля уменьшается в среднем на 1000 у.е., а только за счет увеличения пробега на 1 тыс. км – на 0,5 у.е.). В-третьих, что, пожалуй, наиболее важно, этот результат позволяет прогнозировать цену на автомобиль, если известны его основные параметры. Теперь менеджеру не составит большого труда определить ожидаемую цену вновь поступившего для продажи автомобиля, даже если его год выпуска и пробег не встречались ранее в данном салоне.
Понятие функциональной и статистической зависимости.
Основные идеи экономики – взаимосвязь между экономическими переменными: спрос на товар на рынке рассматривается как функция его цены, затраты на изготовление какого-либо продукта – функция от объема производства, потребительские расходы – функция дохода и т.д. Это примеры взаимосвязей между двумя переменными, одна из которых (спрос на товар, производственные затраты, потребительские расходы) является объясняемой переменной (результирующим показателем), а другая (цена, объем производства, доход) – объясняющей переменной (фактор).
Проблема изучения взаимосвязей экономических показателей является одной из важнейших проблем экономического анализа.
Среди многих форм связей явлений важнейшую роль играет причинная, определяющая все другие формы. Сущность причинности состоит в порождении одного явления другим. В любой конкретной связи одни признаки выступают в качестве факторов, воздействующих на другие и обуславливающие их изменение, другие – в качестве результатов действий этих факторов. Иными словами, одни представляют собой причину, другие – следствие. Признаки, характеризующие следствие, называются результативными (зависимыми, объясняемыми переменными  ), признаки, характеризующие причины – факторными (независимыми, объясняющими переменными
), признаки, характеризующие причины – факторными (независимыми, объясняющими переменными  ).
).
Изучение зависимостей экономических переменных начнем со случая двух переменных (обозначим их  и
и  ).
).
Различают два типа зависимости между явлениями и их признаками: функциональную (детерминированную) (например, зависимость выработки продукции на одного рабочего от объёма выпущенной продукции и численности рабочих), и статистическую (например, зависимость между производительностью труда и себестоимостью единицы продукции).
Функциональная зависимость – это связь, при которой каждому значению независимой переменной  соответствует точно определенное значение зависимой переменной
соответствует точно определенное значение зависимой переменной  . Функциональная зависимость чаще всего встречается в естественных науках, реже подобные связи наблюдаются в общественной жизни, в частности в экономических процессах.
. Функциональная зависимость чаще всего встречается в естественных науках, реже подобные связи наблюдаются в общественной жизни, в частности в экономических процессах.
Для социально-экономических явлений характерно то, что наряду с существенными факторами на них оказывают воздействие многие другие, в том числе случайные факторы. В связи с этим существующая зависимость не проявляется здесь в каждом отдельном случае, как при функциональных связях, а лишь «в общем и среднем» при большом числе наблюдений. В этом случае говорят о статистической (стохастической, вероятностной) зависимости.
Статистическая зависимость – это связь, при которой каждому значению независимой переменной  соответствует множество значений зависимой переменной
соответствует множество значений зависимой переменной  , причём неизвестно заранее, какое именно значение примет
, причём неизвестно заранее, какое именно значение примет  .
.
Пусть, например, 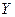 – вес мужчин одного возраста, а
– вес мужчин одного возраста, а  – их рост. Зависимость между
– их рост. Зависимость между 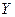 и
и  не является функциональной, т.к. вес разных мужчин одного и того же роста различный, но изменение величины
не является функциональной, т.к. вес разных мужчин одного и того же роста различный, но изменение величины  ведет к изменению заданного распределения величины
ведет к изменению заданного распределения величины 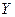 – веса. Зависимость между
– веса. Зависимость между 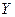 и
и  является статистической.
является статистической.
Можно указать два типа взаимосвязей между переменными  и
и  . В одном случае может быть неизвестно, какая из двух переменных является независимой, а какая - зависимой. В этом случае переменные равноправны, и имеет смысл говорить о статистической взаимосвязи корреляционного типа. Статистическая зависимость, у которой при изменении одной из величин изменяется среднее значение другой величины, называется корреляционной.
. В одном случае может быть неизвестно, какая из двух переменных является независимой, а какая - зависимой. В этом случае переменные равноправны, и имеет смысл говорить о статистической взаимосвязи корреляционного типа. Статистическая зависимость, у которой при изменении одной из величин изменяется среднее значение другой величины, называется корреляционной.
Другая ситуация возникает, если две исследуемые переменные не равноправны: одна из них рассматривается как независимая, а другая как зависящая от первой. Если это так, то изменение одной из переменных служит причиной для изменения другой. Пусть, например, 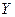 – урожай участка,
– урожай участка,  – количество внесенных удобрений. Зависимость между
– количество внесенных удобрений. Зависимость между 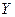 и
и  не является функциональной, т.к. на равных участках земли при равном количестве удобрений снимают все же различный урожай. Это связано с тем, что урожай зависит от многих случайных факторов. Тем не менее, опыт показывает, что средний урожай зависит от количества удобрений. Следовательно, случайные величины – урожай и количество внесенных удобрений – связаны корреляционной зависимостью. Это – тот случай, когда должно быть оценено уравнение регрессии. Уравнение регрессии – это формула статистической связи между переменными:
не является функциональной, т.к. на равных участках земли при равном количестве удобрений снимают все же различный урожай. Это связано с тем, что урожай зависит от многих случайных факторов. Тем не менее, опыт показывает, что средний урожай зависит от количества удобрений. Следовательно, случайные величины – урожай и количество внесенных удобрений – связаны корреляционной зависимостью. Это – тот случай, когда должно быть оценено уравнение регрессии. Уравнение регрессии – это формула статистической связи между переменными:  . Здесь:
. Здесь: 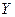 - наблюдаемое значение зависимой переменной,
- наблюдаемое значение зависимой переменной,  - объясненная часть, зависящая от значений объясняющих переменных,
- объясненная часть, зависящая от значений объясняющих переменных,  - случайная составляющая. При корреляционной связи изменение результативного признака
- случайная составляющая. При корреляционной связи изменение результативного признака  обусловлено влиянием факторного признака
обусловлено влиянием факторного признака  не всецело, а лишь частично, т.к. возможно влияние прочих факторов.
не всецело, а лишь частично, т.к. возможно влияние прочих факторов.
Наиболее распространенной формализацией стохастической зависимости между результирующим показателем  и объясняющими переменными (факторами)
и объясняющими переменными (факторами)  в экономике является аддитивная линейная форма:
в экономике является аддитивная линейная форма:
 ,
,
где  - некоторые параметры (обычно неизвестные до проведения соответствующего статистического анализа),
- некоторые параметры (обычно неизвестные до проведения соответствующего статистического анализа),  - случайная составляющая, характеризующая разницу между модельным и наблюденным значениями анализируемой результирующей переменной.
- случайная составляющая, характеризующая разницу между модельным и наблюденным значениями анализируемой результирующей переменной.
Под модельным значением результирующей переменной  понимают её значение, восстановленное по заданным величинам объясняющих переменных при условии, что коэффициенты
понимают её значение, восстановленное по заданным величинам объясняющих переменных при условии, что коэффициенты  известны:
известны:
