Глава 2. Основные теоремы.
Глава 2. Основные теоремы.
Вариант 1.
- В ящике 10 деталей, из которых 4 окрашены. Сборщик наудачу взял 3 детали. Найти вероятность того, что хотя бы одна из взятых деталей окрашена.
- Студент разыскивает нужную ему формулу в трех справочниках. Вероятности того, что формула содержится в первом, втором, третьем справочнике, соответственно равны 0,6; 0,7; 0,8. Найти вероятности того, что формула содержится: а) только в одном справочнике, б) только в двух справочниках, в) во всех трех справочниках.
- В мешочке содержится 10 одинаковых кубиков с номерами от 1 до 10. Наудачу извлекают по одному 3 кубика. Найти вероятность того, что последовательно появятся кубики с номерами 1, 2, 3, если кубики извлекаются: а) без возвращения; б) с возвращением (извлеченный кубик возвращается в мешочек).
- Три исследователя, независимо один от другого, производят измерения некоторой физической величины. Вероятность того, что первый исследователь допустит ошибку при считывании показаний прибора, равна 0,1. Для второго и третьего исследователей эта вероятность соответственно равна 0,15 и 0,2. Найти вероятность того, что при однократном измерении хотя бы один из исследователей допустит ошибку.
- В вычислительной лаборатории имеются 6 клавишных автоматов и 4 полуавтомата. Вероятность того, что за время выполнения некоторого расчета автомат не выйдет из строя, равна 0,95; для полуавтомата эта вероятность равна 0,8. Студент производит расчет на наудачу выбранной машине. Найти вероятность того, что до окончания расчета машина не выйдет из строя.
- Два автомата производят одинаковые детали, которые поступают на общий конвейер. Производительность первого автомата вдвое больше производительности второго. Первый автомат производит в среднем 60% деталей отличного качества, а второй – 84%. Наудачу взятая с конвейера деталь оказалась отличного качества. Найти вероятность того, что эта деталь произведена первым автоматом.
7. В пирамиде 10 винтовок, из которых 4 снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с оптическим прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,8. Стрелок поразил мишень из наудачу взятой винтовки. Что вероятнее: стрелок стрелял из винтовки с оптическим прицелом или без него?
- У рыбака есть 3 излюбленных места рыбалки. Эти места он посещает с одинаковой вероятностью. Вероятность того, что рыба клюнет в первом месте, 1/3, во втором –1/2, в третьем –1/4. Известно, что рыбак забросил удочку 3 раза, а вытащил только одну рыбу. Какова вероятность того, что он рыбачил в первом из его излюбленных мест?
- Рабочий обслуживает 5 станков. 20% времени он уделяет первому станку, 10% – второму, 18% – третьему, 25% – четвертому и 30% – пятому станку. Какова вероятность того, что случайно заглянувший в цех мастер найдет рабочего:
а) у первого или третьего станка;
б) у первого или пятого станка;
в) у первого или четвертого станка;
г) у первого, у второго или у третьего станка?
Глава 2. Основные теоремы.
Вариант 2.
- Для сигнализации об аварии установлены два независимо работающих сигнализатора. Вероятность того, что при аварии сигнализатор сработает, равна 0,95 для первого сигнализатора и 0,9 для второго. Найти вероятность того, что при аварии сработает только один сигнализатор.
- Вероятности того, что нужная сборщику деталь содержится в первом, втором, третьем, четвертом ящике, соответственно равны 0,6; 0,7; 0,8; 0,9. Найти вероятности того, что деталь содержится: а) не более чем в трех ящиках, б) не менее чем в двух ящиках.
- Студент знает 20 из 25 вопросов программы. Найти вероятность того, что студент знает предложенные ему экзаменатором три вопроса.
- Для разрушения моста достаточно попадания одной авиационной бомбы. Найти вероятность того, что мост будет разрушен, если на него сбросить 4 бомбы, вероятности попадания которых соответственно равны: 0,3; 0,4; 0,6; 0,7.
- В пирамиде пять винтовок, три из которых снабжены оптическим прицелом. Вероятность того, что стрелок поразит мишень при выстреле из винтовки с прицелом, равна 0,95; для винтовки без оптического прицела эта вероятность равна 0,7. Найти вероятность того, что мишень будет поражена, если стрелок произведет один выстрел из наудачу взятой винтовки.
- Число грузовых автомашин, проезжающих по шоссе, на котором стоит бензоколонка, относится к числу легковых машин, проезжающих по тому же шоссе как 3:2. Вероятность того, что будет заправляться грузовая машина, равна 0,1; для легковой машины эта вероятность равна 0,2. К бензоколонке подъехала для заправки машина. Найти вероятность того, что это грузовая машина.
- Две из четырех независимо работающих ламп прибора отказали. Найти вероятность того, что отказали первая и вторая лампы, если вероятности отказа первой, второй, третьей и четвертой ламп соответственно равны p1=0,1; p2=0,2; p3= 0,3 и p4=0,4.
- Путешественник может купить билет в одной из трех касс железнодорожного вокзала. Вероятность того, что он направится к первой кассе,
 , ко второй –
, ко второй – 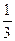 к третьей –
к третьей – 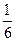 . Вероятности, того, что билетов уже нет в кассах, такие: в первой кассе
. Вероятности, того, что билетов уже нет в кассах, такие: в первой кассе  , во второй –
, во второй – 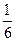 , в третьей –
, в третьей –  . Путешественник обратился в одну из касс и получил билет. Определите вероятность того,что он направился к первой кассе.
. Путешественник обратился в одну из касс и получил билет. Определите вероятность того,что он направился к первой кассе.
9. Два зенитных орудия ведут огонь по одному и тому же самолету. Вероятность попадания выстрелом из первого орудия 0,2, из второго – 0,6. Первым залпом в самолет попали только из одного орудия. Какова вероятность того, что промахнулся расчет первого орудия?
Глава 2. Основные теоремы.
Вариант 3.
- Отдел технического контроля проверяет изделия на стандартность. Вероятность того, что изделие стандартно, равна 0,9. Найти вероятность того, что из двух проверенных изделий только одно стандартно.
- Брошены три игральные кости. Найти вероятности следующих событий: а) на каждой из выпавших граней появится 5 очков; б) на всех выпавших гранях появится одинаковое число очков.
- В урне имеется 5 шаров с номерами от 1 до 5. Наудачу по одному извлекают 3 шара без возвращения. Найти вероятность следующего события: последовательно появятся шары с номерами 1, 4, 5.
- Устройство содержит 2 независимо работающих элемента. Вероятности отказа элементов соответственно равны 0,05 и 0,08. Найти вероятность отказа устройства, если для этого достаточно, чтобы отказал хотя бы один элемент.
- В ящике содержится 12 деталей, изготовленных на заводе № 1, 20 деталей – на заводе № 2 и 18 деталей – на заводе № 3. Вероятность того, что деталь, изготовленная на заводе № 1, отличного качества, равна 0,9; для деталей, изготовленных на заводах № 2 и № 3, эти вероятности соответственно равны 0,6 и 0,9. Найти вероятность того, что извлеченная наудачу деталь окажется отличного качества.
- Две перфораторщицы набили на разных перфораторах по одинаковому комплекту перфокарт. Вероятность того, что первая перфораторщица допустит ошибку, равна 0,05; для второй перфораторщицы эта вероятность равна 0,1. При сверке перфокарт была обнаружена ошибка. Найти вероятность того, что ошиблась первая перфораторщица. (Предполагается, что оба перфоратора были исправны.)
- Три стрелка произвели залп, причем две пули поразили мишень. Найти вероятность того, что третий стрелок поразил мишень, если вероятности попадания в мишень первым, вторым и третьим стрелками соответственно равны 0,6, 0,5 и 0,4.
- При разрыве снаряда образуются осколки трех весовых категорий: крупные, средние и мелкие, причем число крупных, средних и мелких осколков составляет соответственно 0,1; 0,3; 0,6 общего числа осколков. При попадании в броню крупный осколок пробивает ее с вероятностью 0,9, средний – с вероятностью 0,2 и мелкий – с вероятностью 0,05. В броню попал один осколок и пробил ее. Найдите вероятности того, что эта пробоина причинена: крупным, средним и мелким осколком.
9. Группе студентов для прохождения производственной практики выделено 30 мест: 15 – в Туле, 8 – во Владимире, 7 – в Калуге. Какова вероятность того, что студент и студентка, которые в скором времени собираются справить свадьбу, будут посланы для прохождения практики в один и тот же город, если декан ничего не знает об их «семейных» делах?