Экзаменационный тест по дисциплине
Варианты тем рефератов
1. Моделирование экономических систем средствами теории массового обслуживания
2. Моделирование экономических систем средствами регрессионного анализа
3. Моделирование экономических систем средствами матричных моделей
4. Моделирование экономических систем средствами динамического программирования
5. Моделирование экономических систем средствами регрессионного и корреляционного анализа.
6. Моделирование экономических систем средствами теории игр в условиях неопределенности.
7. Моделирование экономических систем средствами целочисленного программирования.
8. Бескоалиционные (некооперативные) и коалиционные (кооперативые) игры.
9. Линейные непрерывные динамические модели макроэкономики.
10. Математические модели микроэкономики: модели поведения потребителей.
Варианты заданий курсовой работы
Вариант 1
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно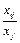 
, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 
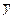объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б)составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли 
;
г) составить матрицу потоков средств производства (xij);
д)найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.)
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 6 штук, а семитонных – не более 18 штук. На перевозку всей продукции по смете выделено не более 60 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 0,5 | 1,5 | 0,5 | |||
| II | ||||||
| III | 2,5 | |||||
| IV | 2,5 | |||||
| Прибыль сj |
Задание № 4.В городе имеются четыре домостроительных комбината (ДСК): А1, А2, А3, А4, и строятся четыре микрорайона: В1, В2, В3, В4. Известны ресурсы каждого ДСК, которые составляют соответственно 14, 20, 26, 41 условных единиц продукции. Известна также потребность в комплектах унифицированных изделий каждого микрорайона, их число составляет 30, 22, 15 и 34 условных единицы соответственно. Известны затраты, связанные с доставкой одного комплекта унифицированных изделий из каждого ДСК в каждый микрорайон, которые заданы матрицей С:
.
Требуется так распределить продукцию ДСК по строящимся микрорайонам, чтобы суммарные затраты, связанные с доставкой всего груза от отправителя к потребителю, были минимальными.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.У фермера имеется поле, которое он может засеять культурами А1, А2, А3 в любой пропорции. Урожайность этих культур зависит от сочетания погодных факторов, главными из которых являются осадки и тепло в летний сезон. По признаку «осадки» лето имеет три градации: Н – нормальное, З – засушливое, Д – дождливое; по признаку «тепло» – две градации: Н – нормальное, Ж – жаркое. Известна урожайность культур А1, А2, А3 (в центнерах) в зависимости от сочетания типов погодных условий, а также рыночная цена этих культур.
| Н, Н | Н, Ж | З, Н | З, Ж | Д, Н | Д, Ж | Цена | |
| А1 | |||||||
| А2 | |||||||
| А3 |
Как нужно действовать фермеру, чтобы получить максимальную прибыль? Решить графоаналитическим методом.
Вариант 2
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 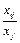, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 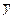объемов продуктов конечного потребления.
, 
.
а)определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в)найти объемы валовой продукции каждой отрасли .
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.);
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.тОрганизации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 18 штук, а семитонных – не более 18 штук. На перевозку всей продукции по смете выделено не более 60 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 0,5 | 0,5 | 0,5 | |||
| II | 2,5 | |||||
| III | 2,5 | |||||
| IV | 2,5 | |||||
| Прибыль сj |
Задание № 4.В пределах города перевозится одинаковый груз их трех пунктов отправления к трем пунктам назначения. Всего отправляется ежедневно 50 т, в том числе из первого пункта – 16 т, из второго – 14 т, из третьего – 20 т. Эти 50 т груза должны поступить в пункты назначения в следующих количествах: в первый пункт – 10 т, во второй – 25 т, в третий – 15 т.
Известны расстояния между пунктами отправления и пунктами назначения, заданные матрицей издержек:
.
Требуется составить план перевозок, обеспечивающий наименьший пробег груза в тонно-километрах.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Фирма производит платья и костюмы, реализация которых зависит от состояния погоды. Затраты фирмы в течение апреля-мая на единицу продукции составят: платья – 5 ден. ед., костюмы – 25 ден. ед. Цена реализации составит 10 ден. ед. и 40 ден. ед. соответственно. По данным наблюдений за несколько предыдущих лет фирма может реализовать в условиях теплой погоды 1 220 платьев и 550 костюмов, при прохладной погоде – 410 платьев и 930 костюмов. В связи с возможными изменениями погоды определить стратегию фирмы в выпуске продукции, обеспечивающую ей максимальный доход. Задачу решить графическим методом и с использованием критерия Гурвица, приняв степень оптимизма 0,4.
Вариант 3
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 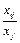, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 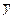объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б)составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли .
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.);
г) составить матрицу потоков средств производства (xij);
д)найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 5 штук, а семитонных – не более 22 штук. На перевозку всей продукции по смете выделено не более 70 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 1,5 | 1,5 | ||||
| II | 0,5 | 0,5 | ||||
| III | 0,5 | 0,4 | ||||
| IV | 1,5 | 2,5 | ||||
| Прибыль сj |
Задание № 4.В резерве трех железнодорожных станций А1, А2, А3 находятся соответственно 60, 80, 100 вагонов. Составить оптимальный план перегона этих вагонов к четырем пунктам хранения зерна, если пункту В1 необходимо 40 вагонов, В2 – 60 вагонов, В3 – 80 вагонов, В4 – 60 вагонов. Стоимости перегонов со станций А1, А2, А3 во все пункты хранения В1, В2, В3, В4 заданы матрицей С:
.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Намечается крупномасштабное производство легковых автомобилей. Имеются четыре варианта проекта автомобиля. По истечении трех сроков Пi (i = 1, 2, 3) рассматриваются как некоторые состояния среды (природы). Экономическая эффективность для различных проектов и состояний природы указана в таблице.
| Проекты | Состояние природы | ||
| П1 | П2 | П3 | |
| А1 | |||
| А2 | |||
| А3 | |||
| А4 |
Выбрать лучший проект легкового автомобиля для производства, используя критерии Вальде, Сэвиджа и Гурвица, при = 0,1. Сравните решения и сделайте выводы.
Вариант 4
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 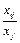, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 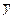объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли .
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.);
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.
Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 12 штук, а семитонных – не более 33 штук. На перевозку всей продукции по смете выделено не более 120 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 0,5 | 0,5 | ||||
| II | 1,5 | |||||
| III | 0,5 | |||||
| IV | ||||||
| Прибыль сj |
Задание № 4.В городе имеются три домостроительных комбината (ДСК): А1, А2, А3, и строятся четыре микрорайона: В1, В2, В3, В4. Известны ресурсы А1 – 100, А2 – 130, А3 – 170 и производственные потребности унифицированных изделий микрорайона: В1 – 150, В2 – 120, В3 – 80, В4 – 50. Известны также затраты, связанные с доставкой одного комплекта унифицированных изделий из каждого пункта комплектования в каждый пункт назначения:
.
Требуется распределить продукцию ДСК по микрорайонам, чтобы суммарные приведенные затраты, связанные с доставкой всего груза от отправителя к потребителю, были минимальны.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Определить тип электростанции, которую необходимо построить для удовлетворения энергетических потребностей комплекса крупных промышленных предприятий. Возможные стратегии: А1 – сооружается гидроэлектростанция; А2 – сооружается теплоэлектростанция; А3 – сооружается атомная станция. Экономическая эффективность сооружения электростанции зависит от влияния случайных факторов, образующих множество состояний природы Sj (j = 1, 2, 3, 4, 5). Результаты экономической эффективности приведены в таблице.
| Тип станции | Состояние природы | ||||
| П1 | П2 | П3 | П4 | П5 | |
| А1 | |||||
| А2 | |||||
| А3 |
Использовать критерии Вальде, Сэвиджа и Гурвица для = 0,3. Сравните решения и сделайте выводы.
Вариант 5
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 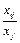, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 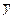объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б)составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли . Расчеты рекомендуется производить с точностью до двух знаков после запятой;
г) составить матрицу потоков средств производства (xij);
д)найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 24 штук, а семитонных – не более 33 штук. На перевозку всей продукции по смете выделено не более 120 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1)построить математическую модель задачи;
2)решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 1,5 | 0,5 | 0,1 | |||
| II | 2,5 | 2,5 | ||||
| III | 2,5 | |||||
| IV | 2,5 | |||||
| Прибыль сj |
Задание № 4.В двух пунктах отправления А1 и А2 находятся соответственно 150 и 90 т горючего. В пункты В1, В2, В3 требуется доставить соответственно 60, 70, 110 т горючего. Стоимость перевозки 1 т горючего определяется в условных единицах и задана в матрице:
.
Составить оптимальный план перевозок горючего, чтобы общая сумма транспортных расходов была минимальной.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Одно из транспортных предприятий должно определить уровень своих провозных возможностей так, чтобы удовлетворить спрос клиентов на транспортные услуги на планируемый период. Спрос на транспортные услуги неизвестен, но ожидается, что он может принять одно из четырех значений: 10, 15, 20 или 25 тыс. т. Для каждого уровня спроса существует наилучший уровень провозных возможностей транспортного предприятия (с точки зрения возможных затрат). Отклонения от этих уровней приводят к дополнительным затратам либо из-за превышения провозных возможностей над спросом (из-за простоя подвижного состава), либо из-за неполного удовлетворения спроса на транспортные услуги.
В таблице указаны возможные прогнозируемые затраты на развитие провозных возможностей.
| Варианты провозных возможностей транспортного предприятия | Варианты спроса на транспортные услуги | |||
Выбрать оптимальную стратегию, используя критерии Вальде, Сэвиджа и Гурвица, при = 0,5. Сравните решения и сделайте выводы.
Вариант 6
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 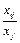, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 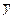объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б)составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли . Расчеты рекомендуется производить с точностью до двух знаков после запятой;
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 36 штук, а семитонных – не более 33 штук. На перевозку всей продукции по смете выделено не более 120 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1)построить математическую модель задачи;
2)решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | ||||||
| II | 1,5 | |||||
| III | 0,5 | 0,5 | 0,5 | |||
| IV | 0,5 | |||||
| Прибыль сj |
Задание № 4.В пределах одного города перевозится одинаковый груз из трех пунктов отправления к трем пунктам назначения. Всего отправляется ежедневно 30 т, в том числе из первого пункта – 12 т, из второго – 8 т, из третьего – 10 т. Эти 30 т груза должны поступить в пункты назначения в следующих количествах: в первый пункт – 6 т, во второй – 9 т, в третий – 15 т. Известны расстояния между пунктами отправления и пунктами назначения:
.
Составить план перевозок, обеспечивающий наименьший общий пробег грузов.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Предприятие выпускает скоропортящуюся продукцию, которую может сразу отправить потребителю (стратегия А1), отправить на склад для хранения (стратегия А2) или подвергнуть дополнительной обработке (стратегия А3) для длительного хранения. Потребитель может приобрести продукцию: немедленно (стратегия В1), в течение небольшого времени (стратегия В2), после длительного периода времени (стратегия В3). В случае стратегий А2 и А3 предприятие несет дополнительные затраты на хранение и обработку продукции, которые не требуются для А1, однако при А2 следует учесть возможные убытки из-за порчи продукции, если потребитель выберет стратегии В2 или В3. Определить оптимальные пропорции продукции для применения стратегий А1, А2, А3 при матрице затрат согласно таблице.
| В1 | В2 | В3 | |
| А1 | |||
| А2 | |||
| А3 |
Решить задачу графоаналитическим методом.
Вариант 7
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 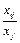, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 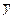объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли . Расчеты рекомендуется производить с точностью до двух знаков после запятой.;
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 24 штук, а семитонных – не более 20 штук. На перевозку всей продукции по смете выделено не более 90 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 0,5 | 1,5 | 0,5 | |||
| II | 2,5 | 0,5 | 1,5 | 0,5 | ||
| III | ||||||
| IV | 2,5 | |||||
| Прибыль сj |
Задание № 4.В пределах города с трех продовольственных баз перевозится груз в четыре магазина. Всего отправляется 300 кг, в том числе с 1-й базы – 90 кг, со 2-й – 130 кг, с 3-й – 80 кг. Эти 300 кг груза должны поступить в магазины в следующих количествах: 60, 100, 50, 90 кг. Известны расстояния между базами и магазинами, заданные в виде матрицы издержек:
.
Составить план перевозок, обеспечивающий наименьший пробег груза.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Руководство универмага заказывает товар. Известно, что спрос на этот товар может принять одно из четырех значений: 6, 7, 8 или 9 ед. Если заказанного товара окажется недостаточно для удовлетворения спроса, то руководство может срочно заказать и завезти недостающее количество. Если же спрос будет меньше наличного количества товара, то нереализованный товар хранится на складе универмага. Определить такой объем заказа на товар, при котором дополнительные затраты, связанные с хранением и срочным завозом, были бы минимальными, если расходы на хранение единицы товара составляют 1 руб., а по срочному заказу и завозу – 2 руб. Использовать критерии Вальде, Сэвиджа и Гурвица при = 0,2.
Вариант 8
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 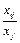, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 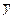объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли .
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.);
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 24 штук, а семитонных – не более 40 штук. На перевозку всей продукции по смете выделено не более 150 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;
6) дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 0,5 | 0,5 | ||||
| II | 0,4 | |||||
| III | 2,5 | |||||
| IV | 0,5 | |||||
| Прибыль сj |
Задание № 4.Три домостроительных комбината (ДСК) производят продукцию для пяти районов города. Производительные ресурсы каждого ДСК составляют 180, 270, 120 условных единиц. Производственные потребности районов города в продукции ДСК – соответственно 125, 140, 50, 80, 125. Известны затраты, связанные с доставкой изделий из каждого ДСК в каждый район города, представленные в виде матрицы издержек:
.
Составить план перевозок, обеспечивающий наименьший пробег груза.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Предприятие может выпускать три вида продукции: А1, А2, А3. Получаемая прибыль зависит от спроса, который может быть в одном из четырех состояний: В1, В2, В3, В4. Задана матрица
,
элементы aij – прибыль, которую получит предприятие при выпуске продукции Аi с состоянием спроса Вj (i = 1, 2, 3; j = 1, 2, 3, 4). Определить оптимальные пропорции выпускаемой продукции, гарантирующие среднюю величину прибыли при любом состоянии спроса.
Задачу решить графоаналитическим методом.
Вариант 9
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 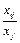, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 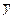объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли .Расчеты рекомендуется производить с точностью до двух знаков после запятой;
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 36 штук, а семитонных – не более 40 штук. На перевозку всей продукции по смете выделено не более 150 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1)составить математическую модель задачи;
2)привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3)решить задачу симплекс-методом;
4)определить количество неизрасходованного сырья при найденном оптимальном плане;
5)построить двойственную задачу, решить ее;
6)дать экономический анализ двойственной задачи, оценить целесообразность введения в план нового вида продукции, если затраты на производство этой продукции и получаемая прибыль заданы в последней графе таблицы.
| Виды продукции Виды сырья | Технологические коэффициенты аij | Запасы сырья | Новый вид продукции | |||
| A | B | C | D | |||
| I | 2,5 | 0,5 | 1,5 | 0,5 | ||
| II | 0,5 | 1,5 | 0,5 | 0,5 | ||
| III | 0,5 | 2,5 | ||||
| IV | 0,5 | 2,5 | ||||
| Прибыль сj |
Задание № 4.На четырех овощных базах имеется продукция, которую необходимо доставить в три магазина согласно поданным ими заявкам в количестве 250, 100, 150 кг соответственно, при этом на первой овощной базе имеется продукции 110 кг, на второй – 140 кг, на третьей – 150 кг, на четвертой – 100. Распределить овощную продукцию среди магазинов так, чтобы все поданные заявки были выполнены, продукция со всех баз реализовалась полностью, расходы на доставку груза были минимальными, если известна матрица транспортных издержек:
.
Задание № 5.Свести матричную игру к задаче линейного программирования:
.
Задание № 6.Объединение производит разведку полезных ископаемых на трех месторождениях. Фонд средств предприятия составляет 10 ден. ед., эту сумму необходимо использовать полностью. Деньги в первое месторождение могут быть вложены в количестве, кратном 2 ден. ед., во второе – 3 ден. ед., в третье – 5 ден. ед. Цены на полезные ископаемые в конце планового периода могут оказаться в двух состояниях: С1 и С2. Эксперты установили, что в ситуации С1 прибыль на месторождении М1 составит 10 % от количества вложенных ден. ед. на разработку, на М2 – 15 % и на М3 – 6 %. В ситуации С2 на конец планового периода прибыль составит 12 %, 7 %, 9 % на месторождениях М1, М2, М3 соответственно. Принять решение о вложении денег в месторождения, чтобы обеспечить наибольшую возможную прибыль от разработки полезных ископаемых. Проанализировать практическую ситуацию по нескольким критериям. Для критерия Гурвица принять = 0,7. Выбрать обоснованное решение.
Вариант 10
Задание № 1.Рассмотрим три отрасли промышленности: I, II, III, каждая из которых производит свой однородный продукт и для обеспечения производства нуждается в продукции других отраслей. Процесс производства рассматривается за определенный период времени (например, за год). Взаимодействие отраслей определяется матрицей А прямых затрат. Число аij, стоящее на пересечении i-й строки и j-го столбца, равно 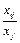, где xij – поток средств производства из i-й отрасли в j-ю, а xj – валовой объем продукции j-й отрасли (все объемы продукции выражаются в единицах стоимости). Задан вектор 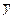объемов продуктов конечного потребления.
, 
.
а) определить, является ли матрица А продуктивной;
б) составить уравнение межотраслевого баланса;
в) найти объемы валовой продукции каждой отрасли .
(Расчеты рекомендуется производить с точностью до двух знаков после запятой.);
г) составить матрицу потоков средств производства (xij);
д) найти объемы валового выпуска продукции, если конечное потребление по отраслям увеличится на 60, 70, 30 соответственно.
Задание № 2.Организации, занимающейся перевозкой и продажей продукции, необходимо перевезти партию товара. При этом можно арендовать для перевозки по железной дороге 5- и 7-тонные контейнеры. Пятитонных контейнеров имеется в наличии не более 10 штук, а семитонных – не более 22 штук. На перевозку всей продукции по смете выделено не более 80 тысяч рублей, причем цена за аренду пятитонного контейнера – 2 тыс. рублей, а семитонного – 3 тыс. рублей. Определить, сколько и каких контейнеров следует арендовать, чтобы общий объем грузоперевозок был максимальным.
Решение задачи оформить поэтапно:
1) построить математическую модель задачи;
2) решить задачу линейного программирования с использованием графического метода.
Задание № 3.Некоторая фирма выпускает четыре вида (различной) продукции, используя четыре вида сырья. В таблице указаны:
§ технологические коэффициенты аij, которые показывают, сколько единиц i-го вида сырья требуется для производства одной единицы j-го вида продукции;
§ прибыль сj, получаемая от производства j-го вида продукции (в нижней строке таблицы);
§ запасы сырья в планируемый период (в тех же единицах).
Составить такой план выпуска продукции, при котором будет обеспечена максимальная прибыль.
Решение задачи оформить поэтапно:
1) составить математическую модель задачи;
2) привести задачу к каноническому виду, пояснить экономический смысл дополнительных переменных;
3) решить задачу симплекс-методом;
4) определить количество неизрасходованного сырья при найденном оптимальном плане;
5) построить двойственную задачу, решить ее;