ОСНОВНІ РІВНЯННЯ МЕХАНІКИ СУЦІЛЬНОГО СЕРЕДОВИЩА

1 Рівняння рівноваги

 

До цього часу ми розглядали напружений стан гірського масиву в окремо взятій точці. При переході до напруженого стану по всьому об’єму необхідно розглянути зв’язок компонентів напружень в найближчих точках об’єму. Фунуцію для цих напружень, які в суцільному середовищі є безперервними функціями координат, розкладемо поблизу точки М (мал. 1) в ряд Тейлора і обмежимося членами 1-го порядку. Тоді компоненти напругжень в нескінченно близькій сусідній точці виражаються через компоненти даної точки лінійними залежностями.

Якщо для точки М твердого тіла виділити елементарний паралелепіпед з нескінченно малими ребрами 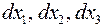та гранями, паралельними координатним площинам, то, як відомо з теоретичної механіки, для його рівноваги повинні задовольнятися наступні рівняння (принцип Даламбера-Ейлера):

 

 

Крім сил, діючих на гранях елементарного паралелепіпеда, врахуємо об’ємні сили, такі як вага та сила інерції.

Перші три умови дозволяють отримати наступні рівняння динамічної рівноваги суцільного середовища:

 

 

(1)

 

де - щільність речовини; , , - проекції об’ємних сил на осі координат, віднесені до одиниці маси; , , - зміщення по осям координат.

Перетворення суми моментів приводить до вказаної раніше умови парності взаємних дотичних напруг:

 

(2)

 

В загальному вигляді ці шість рівнянь можна записати:

 

(3)

 

(4)

 

У випадку статичної рівноваги рівняння (3) спрощуються

 

(5)

 

При плоскій деформації можна записати:

 

(6)

Рівняння (3) має 9 невідомих функцій . Тобто, для визначення всіх невідомих потрібно додатково щонайменше ще 6 рівнянь.

 

2 Рівняння сумісності

 

Такими відсутніми додатковими рівняннями є рівняння, що зв’язують компоненти тензора деформації з кампонентами переміщення

 

(7)

 

У випадку малих деформацій маємо лінійні співвідношення:

 

(Рівняння Коши) (8)

 

При статичній рівновазі переміщення в рівняннях (1) відсутні або незмінні, тому рівняння (8) необхідно перетворити таким чином, щоб знайти безпосередній зв’язок між компонентами деформації.

Цей зв’язок установлено вперше Сен-Венаном у вигляді рівняньсумісності :

 

 

(9)

Введення рівнянь (8) в динамічному і (9) в статичному випадках додало до трьох рівнянь рівноваги (1) ще шість і збільшело їх кількість до дев’яти, а кількість невідомих збільшилося до 15. Отже теорія суцільного середовища в розглянутій постановці не в змозі описати напружений стан масиву. Невистачаючі 6 рівнянь отримують додатково із феноменологічних фізичних теорій: теорії пружності, теорії пластичності, теорії текучості, граничного напруженого стану та таке інше.

Якщо врахувати і квадратичні члени рівнянь (8), то отримаємо: