Модели основных фаз преобразования

Раздел 2. элементы теории информации

Лекция 5. Фазы информационного цикла и их модели

Фазы информационного цикла.

Модели основных фаз преобразования информации.

Литература: 1. Советов Б.Я. Информационная технология: Учеб. для

вузов по спец. «Автоматизир. системы обработки информ.

и упр.». – М.: Высш. шк., 1994.

 

 

Фазы информационного цикла

 

Как было отмечено на предыдущих лекциях, информационные технологии направлены на формирование и рациональное использование информационного ресурса общества. Перед человечеством стоит громадная по своей важности и сложности задача:извлечь максимум информации из накопленных за всю историю своего существования сообщений и превратить ее в активно функционирующий ресурс.Речь идет, в первую очередь, о превращении книжных описаний и других "рассеянных" знаний в алгоритмы и программы. Это лишь часть работ по формированию информационного ресурса.

Сам по себе информационный ресурс не может двигать системы и механизмы. Движителями систем выступают материальные силы: энергетические и трудовые факторы. Но информационный ресурс, словно фермент, переводит эти материальные факторы из латентного в активное состояние и вводит их в заданное русло. Тем самым информационный ресурс обеспечивает прирост свободной энергии в целенаправленных системах социальной природы за счет снижения их энтропии (неопределенности состояния системы).

Особую роль информация, информационный ресурс играют в АСУ. Рассмотрим последовательно основные фазы преобразования информации в автоматизированных системах как составляющие единого информационного процесса.

 

Сбор информации.

Фаза сбора информации является начальным этапом формирования осведомляющей информации. Сбор осущест­вляется либо с датчиков информации, встроенных в технологичес­кие или производственные процессы, с контрольно-измерительных приборов либо путем съема данных графиков, чертежей, схем, номенклатур, прейскурантов, спецификаций и т. д.

В общем случае сигналы, поступающие от объекта, можно разделить на статичес­кие,отображающие устойчивые состояния объектов, и динамичес­кие,для которых характерно быстрое изменение во времени, отоб­ражающее, например, изменение электрических параметров систе­мы. Статические сигналыобычно фиксируются в документальной форме, динамические — появляются на выходе датчиков, контроль­но-измерительных приборов и т. д. По характеру изменения сигналы делятся на непрерывные и дискретные.

На рис. 1 представлена структур­ная схема реализации фазы сбо­ра информации. С технологичес­кого оборудования (ТО) с помо­щью датчиков Д₁ ... Д_nснимается непрерывная информация, которая подвергается операциям преобразования и кодирования. Эти операции выполняются преобразователями Пр₁, ... Пр_n.

 

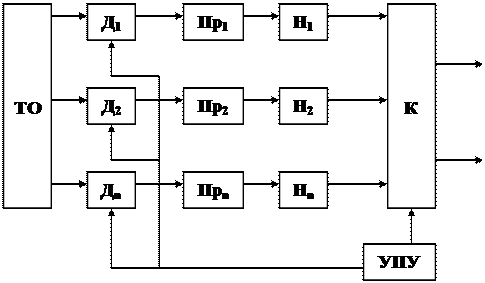
Рисунок 1 – Структурная схема процесса сбора информации

 

При преоб­разовании осуществляется дискретизация непрерывной величины. Эту операцию могут выполнять и датчики. При кодировании дискретное значение непрерывной величины превращается в код. Под кодомпонимают определенный набор символов и знаков, однозначно отображающих любое сообщение, в том числе дискретизированное или мгновенно снятое с датчика значение непрерыв­ной величины. Физически код представляет собой некоторую последовательность импульсов, распределенных во времени либо в пространстве. Он включает в себя ряд элементов, каждый из которых содержит определенное количество информации (в соот­ветствии со статистической мерой). Представленные в кодирован­ном виде значения исходной информации хранятся в накопительных устройствах Н₁ ... Н_nи через коммутатор (К) по определенному закону выводятся на следующую фазу преобразования инфор­мации. Режим опроса, т. е. функционирования коммутатора, задает­ся устройством программного управления (УПУ). При этом могут реализовываться режимы циклического опроса, случайного поиска, опроса по загрузке накопителей, а также по заданным приоритетам.

Рассмотрим отдельные, наиболее характерные для фазы сбора информации процедуры кодирования с использованием неизбыточных кодов.

Процедуры считывания информации с датчика и последующего кодирования зачастую удается совместить. Для уменьшения ошиб­ки считывания при наличии аналого-кодовых преобразователей ис­пользуют специальные виды кодов. Примером является код Грея. Он относится к числу двоичных кодов и обеспечивает высокую точность преобразования непрерывной величины в код. Применяет­ся для отображения десятичных чисел, поэтому используется число комбинаций М = 10 < 2⁴, т. е. код содержит четыре элемента. Так как код двоичный, то каждый элемент четырехэлементного кода может принимать значения «0», «1». Последовательность выбора кодовых комбинаций определяется тем, что при изменении непрерывной величины каждый последующий отсчет непрерывной функции дол­жен отображаться кодовой комбинацией, отличающейся от пре­дыдущей лишь в одном разряде. Это позволяет свести ошибку считывания к единице в младшем разряде. Десятичные числа и от­ображающие их коды представлены в табл. 1.

 

Таблица 1

Десятичное число	Двоичный код	Код Грея	Десятичное число	Двоичный код	Код Грея

 

При сборе информации используются известные неизбыточные коды. В зави­симости от закона распределения снимаемых мгновенных значений непрерывной величины эти коды имеют постоянную либо перемен­ную длину. Если мгновенные значения равновероятны, то наилучшим отображением их в кодированном виде будет представление равномерным кодом. В этом коде все комбинации имеют одинаковую длину и любое сообщение отображается одним и тем же числом символов.

Если отсчеты функции неравновероятны, то для получения наибольшей информативности каждого элемента кода используют неравномерные коды, получившие название статистических кодов. В этих кодах длина комбинации тем больше, чем меньше вероятность возникновения отсчета функции.

Таким образом, при сборе информации существенными оказываются процедуры опроса датчиков и преобразования неэлектрической величины в электрическую, представляемую в виде равномерного или неравномерного кода в зависимости от статистики отсчетов непрерывной функции. При территориально разнесенных датчиках фаза сбора информации может совмещаться с фазой передачи. Тогда возникают проблемы кодирования сигналов с помощью избыточного кода, используемого в фазе передачи информации.

Подготовка информации.

Фаза подготовки информации заключа­ется в записи информации, снятой автоматически с объекта управ­ления либо полученной оператором, на носитель с целью включения этой информации в процесс управления. Вид представления инфор­мации на выходе фазы подготовки зависит от того, с какой следу­ющей фазой сопрягается подготовка информации. Если эта инфор­мация после ее подготовки должна быть передана в канал связи, то необходимо представить ее в виде электрического сигнала, способ­ного передаваться по физической линии либо специально организо­ванному каналу связи. Если за фазой подготовки следует обработка либо хранение информации, то необходимо информацию перенести на машинный носитель либо документ в соответствии с теми прави­лами, которые определяются последующими фазами информацион­ного процесса. Одним из важнейших условий фазы подготовки информации является максимальная автоматизация выполнения процедур подготовки.

При подготовке задач к решению на современных ЭВМ (компьютерах) команды могут записываться в двоичных ходах. В этом же виде они хранятся в памяти ЭВМ. При этом составляется программа, которая записывается в так называемом машинном языке. Процесс кодирования команд на машинном языке получил название программирования. Символичес­кое обозначение всех команд называют языком Ассемблер,а машин­ную программу, по которой выполняется перевод с языка Ассемблер на машинный язык, называют Ассемблером. Надо отметить, что программировать в машинном языке, т. е. в двоичных кодах, трудоем­ко. Подготавливать информацию в таком виде сложно также из-за возможности наличия ошибок. Поэтому при подготовке информации в персональных ЭВМ пользуются более общими языками, когда информация записывается в символическом виде. При вводе информация преобразуется в двоичный код автоматически с помощью специальной программы, существующей в ЭВМ. Это ускоряет процесс программирования.

Следует отметить, что вычислительный процесс внутри ЭВМ, например арифметическая обработка, выполняется в машинных двоичных кодах. При вводе информации функцию кодирующего устройства, в частности, исполняет клавиату­ра.

Таким образом, в современных условиях подготовка информации, если она не связана непосредственно с последующей ее передачей, означает подготовку программ и ввод информации через клавиатуру. Характерно, что и в этом случае автоматизация фазы подготовки информации осуществляет­ся за счет процедуры кодирования, которая реализуется аппарат­ным или программным путем.

 

Передача информации.

Фаза передачи информации в информаци­онном процессе автоматизированной системы возникает тогда, ког­да существует взаимодействие между территориально удаленными объектами. В этом случае между источником и потребителем информации существует канал связи, и возникает задача пере­дачи заданного объема информации через канал связи с требуемой помехоустойчивостью. Сообщение, формируемое источником ин­формации, подвергается на передающей стороне трем проце­дурам: преобразованию, что выполняется преобразователем; кодированию, осуществляемому кодирующим устройством; модуляции, что реализуется модулятором.

На прием­ной стороне над сигналом, который прошел через линейные со­гласующие устройства в канал связи, выполняются сле­дующие процедуры: демодуляция с помощью демодулятора; декодирование, что реализует декодирующее устройство; преобразование полученной информации в соответст­вующую форму, что выполняет потребитель информации.

Особенностью процесса передачи является то, что сигнал, отоб­ражающий код, в канале связи подвергается действию помех. Для обеспечения требуемой помехоустойчивости передачи информации предусматривают введение избыточности как в передаваемый сиг­нал, так и в код. Введение избыточности в передаваемый сигнал осуществляется за счет модуляции. Помехоустойчивость кода обес­печивается избыточным кодированием, которое является основным средством автоматизации фазы передачи информации.

Качество передачи информации оцени­вается вероятностно-временными характеристиками с учетом дейст­вующих помех в каналах связи, надежности элементов аппаратуры и условий обслуживания пересекающихся информационных потоков в концентраторах и узлах коммутации.

Таким образом, фаза пере­дачи информации в информационном процессе АСУ является ис­ключительно ответственной и требует серьезной проработки как на логическом, так и на физическом уровнях реализации системы. Фаза передачи информации обычно предшествует фазе обработки.

 

Обработка информации.

Термин «обработка информации» явля­ется широким. Полезно выделить как подэтап предварительную обработку информации. При автоматизированном управлении це­лью обработки является решение с помощью ЭВМ вычислительных задач оптимизационного либо расчетного характера, отображаю­щих функциональные задачи управления в системе. В этих условиях должны существовать модели обработки информации, соответст­вующие принятым алгоритмам управления. Можно считать, что в памяти ЭВМ хранится некоторая концептуальная модель — ин­формационный образ объекта управления и модели процесса управ­ления. Для обработки необходимо создать набор вычислительных алгоритмов с программным обеспечением, проблемно-ориентиро­ванным на задачи управления.

На этапе предварительной обработ­ки основной задачей является выявление смысла принятого сообще­ния. Семантическое содержание сообщения и его прагматическое значение зависят от пользователя, т. е. потребителя информации. Поэтому должно существовать правило интерпретации сообщения, которое принято по согласованию между источником информации и потребителем. Конкретное содержание процесса предварительной обработки зависит от конечной цели и может быть различным, например, для обнаружения сигнала, обработки текстовой инфор­мации, сжатия измерительной информации и т. д.

В АСУ обработка информации автоматизирована. Эта операция является обязательной составляющей АСУ. Прежде всего, необходимо обработать информацию, входящую во внешнее информационное обеспечение, т. е. ту, которая представлена в формализованном (документаль­ном) виде. Показатели, содержащиеся в документах, обрабатыва­ются в различных подразделениях предприятия. Одной из задач создания системы обработки является рациональное распределение вычислительных ресурсов между подразделениями с целью мини­мизации информационных потоков между службами предприятий и минимизация времени решения вычислительных задач. Вычис­лительные задачи, поставленные на основе данных, представленных в документах, имеют обычно рутинный (информационный) харак­тер. Их решают на ЭВМ на базе типовых вычислительных алгорит­мов. Ряд задач в АСУ, связанных с прогнозированием, стратегичес­ким планированием и управлением, решаются путем моделирова­ния с использованием математических и имитационных моделей. В этих случаях возможна оптимизационная постановка задачи и по­лучение значительного экономического эффекта от реализации ав­томатизированного управления. Несмотря на внешнюю разнотип­ность задач обработки информации, физическая реализация процес­са обработки означает представление данных в ЭВМ с помощью машинных кодов и выполнение ряда типовых операций над дан­ными.

Рассмотрим внутримашинные процедуры обработки информации в ЭВМ.

Характерным процессом обработки в ЭВМ является арифмети­ческая обработка. Она базируется на использовании двоичных ко­дов и выполнении в них операций сложения и вычитания. Процесс арифметической обработки информации в ЭВМ наряду с представлением данных включает в себя представление арифметических команд, соответствующие программы арифметических операций, организацию пересылки информации из одной области памяти в другую и т. д.

К обработке информации следует отнести обработку сигналов в некоторых областях науки и техники, переработку текстовой информации, обработку сообщений, обработку изображений и т. д.

Обработка информации в частных ее проявлениях может входить в отдельные стадии других фаз информационного процесса. Фаза обработки информации тесно связана с фазой хранения.

 

Хранение информации.

Хранение информации можно рассматривать как передачу информации во времени. Различают оперативное и долго­временное хранение информации. Носители информации можно разделить на оперативные и долговременные запоминающие устрой­ства. Необходимость хранения информации в ЭВМ связана не только с процессом арифметической обработки. При управлении создают информационные массивы, которые хранятся в информационной базе. Вопросы хранения информации, принципы организации информацион­ных массивов, поиска, обновления, представления информации приоб­ретают самостоятельный характер. Хранение информации осуществля­ется на специальных носителях.

Фаза хранения информации может быть представлена на кон­цептуальном, логическом и физическом уровнях. Концептуальный уровеньотражает содержательно информацию и способы реализа­ции ее хранения. Логический уровеньопределяет порядок представ­ления информации, организацию информационных массивов. Физи­ческий уровеньозначает реализацию хранения информации на конк­ретных физических носителях. Автоматизация фазы хранения ин­формации осуществляется за счет процессов кодирования, процедур организации информационных массивов, алгоритмизации процес­сов ввода, поиска, вывода и обновления информации.

При хранении в автоматизированных системах, прежде всего, нужно различать информацию, хранимую вне ЭВМ, т. е. в форме документов, и ин­формацию, хранимую внутри ЭВМ, с помощью специальных запо­минающих устройств. На концептуальном уровне сведения о тех­нико-экономическом объекте задают некоторый информационный образ. Этот образ отражается в виде технико-экономической инфор­мации, куда входят сведения наблюдателя об управляемом объекте, а также информация, которой обменивается этот объект с внешней средой. Ввиду большого объема технико-экономической информа­ции необходимо компактное ее представление. Для этого использу­ют процедуру классификации и кодирования.

Наряду с классификаци­ей и кодированием существенным этапом автоматизации хранения информации является организация информационных массивов. Объекты и явления реального мира в ЭВМ представляются на стадии хранения информации в виде данных, при этом нам важны не только данные, но и связи между ними, т. е. принцип их ор­ганизации. Желательно, чтобы концептуальная структура данных отображала реальные явления окружающего нас мира. Однако на физическом уровне структура данных во многом определяется требованиями, накладываемыми возможностями технических средств хранения информации.

Наиболее простой является линей­ная структура хранения. Организация данных может быть выпол­нена в виде строки, одномерного массива, стека, очереди и т. д. При организации данных в виде строки элементы данных располагаются по признаку непосредственного следования, т. е. по мере поступления данных в ЭВМ. В случае одномерного массива отдельные его элементы имеют индексы, т. е. поставленные им в соответствие целые числа. Эти числа можно рассматривать как номер элемента массива. Наличие индекса позволяет получить до­ступ к заданному элементу, и это оказывается намного проще, чем осуществлять поиск требуемого элемента в строке. С учетом дина­мики процесса ввода и вывода информации различают также струк­туры данных, в которых используется линейный принцип организа­ции, реализующий дисциплину обслуживания «последним при­шел — первым ушел». Такая структура получила название стека. В стеке первым удаляется последний поступивший элемент. Воз­можна реализация и другой дисциплины обслуживания, при кото­рой для обработки информации выбирается элемент, поступивший ранее всех других. Такая структура получила название очереди. Рассмотренные структуры от­носятся к линейным и отображают достаточно простые одномерные структуры данных.

В случае многомерных сложных структур возникают и нелинейные структуры хранения данных. К ним можно отнести многомерные массивы, отображаемые деревьями, графами, сетями. Элемент многомерного массива также определяется индек­сом, однако индекс состоит из набора чисел. В основе формального представления многомерного прямоугольного массива лежит мат­рица, а в матрице каждое ее значение определяется совокупностью чисел, что и составляет индекс требуемого элемента массива.

Организация расположения данных может быть представлена на логическом уровне, при этом возникают логические структуры ин­формационных массивов. Данные компонуются в виде записей, которые в информационном массиве могут располагаться различ­ным образом. Выделяют четыре основные структуры информаци­онных массивов на логическом уровне: последовательную, цепную, ветвящуюся, списковую.

В последовательной структуре записи информационного массива располагаются последовательно, нахождение требуемой записи осуществляется путем просмотра всех предшествующих. Включение новой записи в информационный массив требует смеще­ния всех записей, начиная с той, которая включается. Обновление информационных массивов при последовательной структуре требу­ет перезаписи всего массива.

В цепной структуре информационные массивы располагают­ся произвольно. Для логической связи отдельных записей необ­ходима их адресация, т. е. каждая предыдущая запись логически связанного информационного массива должна содержать адрес рас­положения последующей записи. В случае, если с определенного уровня, т. е. признака, значения в записях повторяются в различных сочетаниях, то возможен переход в целях экономии памяти от цепной структуры к ветвящейся.

В ветвящейся структуре сначала в информационном массиве размещается запись, отображающая признак объекта с небольшим числом значений, далее эти значения повторяются в записях в раз­личных сочетаниях, т. е. возможно от некоторой основной записи переходить к другим в зависимости от запроса, не повторяя основ­ную запись. Чтобы устранить повторяющиеся записи и соответст­вующие им поля в памяти, их удаляют из основного массива и объединяют в дополнительный небольшой информационный мас­сив. Здесь эти записи упорядочиваются также по какому-то призна­ку без повторений. Тогда в основном массиве вместо удаленного информационного поля указываются адреса записей, которые раз­мещены в дополнительном массиве. Данная структура является удобной при реорганизации информационной базы, поскольку по­вторяющиеся записи легко могут быть заменены, так как они хранятся в дополнительном массиве, основной же массив подверга­ется при этом малому изменению. Однако эта структура требует дополнительного объема памяти.

Списковая структура информационных массивов характери­зуется наличием списка, который содержит набор данных, опреде­ляющий логический порядок организации информационного мас­сива. Список включает имя, поля данных и адреса полей. В памяти ЭВМ элементы списка физически разнесены, но связаны друг с дру­гом логически за счет адресных ссылок. Поле данных в зависимости от характера хранимой информации может представляться двоич­ным разрядом, словом фиксированной либо переменной длины, а также набором отдельных слов. Формализовано список может быть представлен в виде таблицы, в которой именам списка и по­лям данных сопоставлены адреса. Адреса выбираются произвольно по мере наличия свободных мест в запоминающем устройстве.

Списковая структура с механизмом адресных ссылок может быть представлена в виде графа древовидной струк­туры. Каждый элемент списка тогда включает в себя маркерное поле, поле данных и адресное поле. Маркерное поле предупреждает, имеется ли ссылка на другой список либо такая ссылка отсутствует. В зависимости от этого в маркерном поле ставится знак минус или плюс. Списки могут отображать и более сложные структуры, чем древовидные. Они могут быть показаны ориентированными графа­ми с петлями, в которых возможна ссылка вперед и назад. Возника­ет так называемый симметричный список, и появляется возмож­ность движения в структуре данных в разных направлениях. Видно, что списковая структура отличается высокой логической простотой, но в связи с адресным обращением к данным время доступа здесь велико, так как каждому элементу списка необходимо иметь ссылку. Соответственно значительно возрастает и объем памяти запомина­ющего устройства (ЗУ), которую требуется иметь в списковой структуре по сравнению с последовательной структурой организа­ции информационных массивов.

На физическом уровне любые записи информационного поля представляются в виде двоичных символов. Обращение к памяти большого объема требует и большой длины адреса.

 

Обработанная информация по требованию пользователя выво­дится из ЭВМ. Устройства вывода позволяют представить инфор­мацию в наглядном для пользователя виде либо выдать на носи­тель для длительного хранения. К типовым устройствам вывода обычно относят световые индикаторы, табло, дисплеи, печатающие устройства, графопостроители и др. На этих устройствах любой вид информации (буквенный, цифровой, графический) может быть пред­ставлен в наглядном и удобном для пользователя виде. Это позво­ляет значительно повысить эффективность работы оператора либо лица, принимающего решения.

Для автоматизации процесса вывода информации используют ее преобразование, кодирование и декодирование. Декодирование осу­ществляется автоматически за счет превращения двоичной инфор­мации в десятичную и в буквенный текст. Существующее типовое периферийное оборудование, а также специализированные устройства вывода позволяют в значительной степени автоматизировать процесс вывода и представления инфор­мации лицу, принимающему решение.

В целом информационный процесс при управлении производством является структурно слож­ным, включает ряд фаз, автоматизация которых реализуется за счет процедур преобразования и кодирования информации.

 

 

Модели основных фаз преобразования

Информации

 

Информационная технология базируется на реализации информационных процессов, разнообразие которых требует выделения базовых, характерных для любой информационной технологии. К ним можно отнести управление, обмен, обработку, накопление данных и формализацию знаний. На логическом уровне должны быть построены математические модели, обеспечивающие объединение процессов в информационную технологию. Модель процесса передачи может быть представлена совокупностью моделей каналов связи и ошибок, являющихся следствием воздействия помех на передаваемые коды сообщений. Модель процесса обработки отображается моделью планирования и моделью реализации вычислений. В ходе обработки на основе входных данных формируются промежуточные и выходные, поэтому существенным становится процесс накопления, в основе которого должны лежать модели, обеспечивающие построение информационной базы.

В условиях персонализации вычислений особую роль играют модели представления знаний. Распространение получили логическая, алгоритмическая, семантическая и фреймовая модели, а также их совместное использование.

Рассмотрим более подробно некоторые из перечисленных моделей.

 

Модель процесса передачи

Взаимодействие между территориально удаленными объектами осуществляется за счет обмена данными. Доставка данных произ­водится по заданному адресу с использованием сетей передачи данных. В условиях распределенной обработки информации эти сети превращаются в информационно-вычислительные, однако и для них остаются характерными проблемы передачи, распределе­ния и доставки данных по заданным адресам. Важнейшим звеном сети является канал передачи данных, структурная схема которого представлена на рис. 2. Физической средой передачи данных явля­ется некоторый реальный либо специально организуемый канал связи (КС), в котором элементы данных передаются в виде физичес­ких сигналов. Такой канал получил название непрерывного канала (НКС), поскольку сигналы описываются непрерывными функциями времени.

 

Рисунок 2 – Структурная схема канала передачи данных

 

Согласование сигнала и канала связи осуществляется по физическим характеристикам, а также по соотношению скорости передачи информации и пропускной способности непрерывного канала. Следует отметить, что большинство непрерывных каналов оказыва­ются непригодными для передачи сигналов, отображающих дан­ные, без предварительного их преобразования. Поэтому сигналы по физическим характеристикам должны быть согласованы со свойст­вами непрерывного канала связи, для чего в структуре канала передачи данных предусматривают устройства преобразования сиг­налов, которые для телефонных каналов связи приобретают харак­тер модемов. Модем представляет собой совокупность модулятора и демодулятора. С помощью модулятора сигнал воздей­ствует на некоторый параметр переносчика, благодаря чему спектр сигнала смещается в область частот, для которых наблюдается наименьшее затухание в выбранном непрерывном канале связи. Обратную операцию, т. е. переход от модулированного сигнала к модулирующему, осуществляет демодулятор. Как показано на рисунке, непрерывный канал связи совместно с функционирующими на его концах модемами образует дискретный канал связи (ДКС).

Канал передачи данных является основ­ной составной частью сети обмена данными, в которой процесс передачи реализуется на основе принятого метода коммутации и принципа маршрутизации данных. Рассмотрим канал передачи данных на логическом уровне. В основе его лежит модель дискрет­ного канала связи.

Дискретный канал связи (ДКС) имеет на входе множество символов кода Xс энтропией источника Н(Х),а на выходе — множество символов Y с энтропией H(Y). Если формируемые символы из множества Xи вы­являемые из множества Y расположить в узлах графа, соединив эти узлы дугами, отображающими вероятности перехода одного сим­вола в другой, то получим модель дискретного канала связи, пред­ставленную на рис. 3. Множество символов X конечно и определя­ется основанием системы счисления кода K_x на входе канала. Систе­ма счисления по выявляемым символам также конечна и составляет К_y. Вероятности переходов, связывающих входные и выходные сим­волы, могут

 

Рисунок 3 – Граф дискретного канала связи с шумом

 

быть записаны в виде матрицы

 

.

 

В этой матрице i- й столбец определяет вероятность выявления на выходе дискретного канала связи символа у_i. Вероятности, расположенные на главной диагонали, называются вероятностями прохождения символов, остальные вероятности есть вероятности трансформации. Анализ модели дискретного канала связи возможен, если известна статистика появления символов на входе канала. Потери информации могут быть вызваны действием помех, которые отображаются в дискретном канале в виде некоторого потока ошибок. Поток ошибок задается с помощью определенной модели ошибок, на основании которой может быть установлена матрица переходов Р. При определенных соотношениях между вероятностями переходов, входящих в матрицу Р, выделяют: симметричные каналы по входу, для которых вероятности, входящие в строку матрицы, являются перестановками одних и тех же чисел; симметричные каналы по выходу, для которых это относится к вероятностям, входящим в столбцы; симметричные каналы по входу и по выходу при соблюдении обоих условий. На основе представленной классификации матрица двоичного симметричного канала имеет вид

 

,

 

где Р – вероятность искажения символа.

Для граничного случая двоичного симметричного канала без шума матрица переходов имеет вид

 

.

 

Пропускная способностьдискретного канала связи без шума составляет

 

С = log₂ K_y,

 

где К_у – основание системы счисления кода на выходе канала.

Пропускная способность двоичногосимметричного канала связи с шумом (то есть при К = 2) составляет

 

C = 1 + (1 - P)log₂ (1 - P) + P log₂ P.

 

Анализ показывает, что при Р = 0 пропускная способность двоичного симметричного канала равна 1, а при Р = 0,5 – С = 0.

 

Модель процесса обработки.

В условиях автоматизированного управления внутримашинная обработка информации предполагает последовательно-параллельное во времени решение вычислительных задач, отображающих функциональные задачи АСУ. Это возможно при наличии определенного плана организации вычислительного процесса, реализуемого на основе имеющихся вычислительных ресурсов ЭВМ. Вычислительная задача, формируемая источником вычислительных задач (ИВЗ), по мере необходимости решения обращается к запросам в вычислительную систему (ВС) (рис. 4)

 

 

Рис. 4

 

Организация вычислительного процесса предполагает определение последовательности решения задач и реализацию вычислений. Последовательность решения задается исходя из их информационной взаимосвязи, когда результаты решения одной задачи используются как исходные данные для решения последующей. Процесс решения определяется принятым вычислительным алгоритмом.

В вычислительной системе можно выделить систему диспетчирования (СД), которая определяет организацию вычислительного процесса, и ЭВМ, обеспечивающую обработку информации.

Каждая вычислительная задача, поступающая в вычислительную систему, может быть рассмотрена как некоторая заявка на обслуживание. Последовательность вычислительных задач во времени создает поток заявок, обслуживание которых может быть математически формализовано некоторым законом распределения времени обслуживания. В соответствии с требованиями на организацию вычислительного процесса возможно перераспределение поступающих задач на основе принятой схемы диспетчирования.

 

Модели обслуживания вычислительных задач.

При наличии плана организации вычислительного процесса основная проблема заключается в обслуживании заявки, которое характеризуется временем пребывания заявки в системе. Это время складывается из времени ожидания в очереди и времени обслуживания, представляющего собой время обработки информации процессором на основе принятой программы. Анализ процесса обслуживания заявки может быть выполнен на основе теории массового обслуживании. Тогда вычислительная система может быть представлена математической моделью системы массового обслуживания, которая характеризуется числом обслуживающих приборов, т. е. ЭВМ, дисциплиной образования очереди, числом вычислительных задач в ИВЗ, дисциплиной обслуживания очереди с помощью диспетчера Д.

В зависимости от того, какое число ЭВМ используется, различают одно- и многолинейные системы. Даже для многолинейной системы может наблюдаться случай, когда все обслуживающие приборы, т. е. ЭВМ, будут заняты. Тогда модель системы может предполагать такой поток заявок, который не ждет обслуживания, и возника­ет система с потерями. Физически это возможно либо когда очередь не предусматривается, либо когда имеется полное заполнение очереди.

Другая модель системы характеризуется тем, что заявка на решение вычислительной задачи, поступившая в вычислительную систему, может ожидать и покидает ее только после полного обслуживания. В реальных вычислительных системах это оказывается возможным благодаря тому, что предусматриваются очереди О₁ — О_N.Так как очередь не может быть не ограниченной, то данная система характеризуется числом заявок, ожидающих начала обслуживания. Возможны дополнительные ограничения на время ожидания, на время пребывания заявки в вычислительной системе и др. Существенное влияние, как на параметры обслуживающей системы, так и на процесс ее анализа, оказывает характер входящею потока заявок. Заявки от ИВЗ образуют во времени поток, который может иметь ограниченное или неограниченное число задач. Paзличными могут быть и правила обслуживания заявок, находящихся в очереди. В соответствии с этим устанавливается некоторая дисциплина обслуживания диспетчером Д. Естественной дисциплиной является дисциплина «первым пришел — первым обслужен». Возможен инверсный подход: «последним пришел — первым обслужен». Допускаются и случайные дисциплины обслуживания, когда заявки из очереди выбираются в произвольном порядке. В ряде случаев заявки обладают приоритетами. Это наиболее характерно для реальных задач АСУ, в которых имеются информационные взаимосвязи. Тогда заявки имеют разную степень важности по времени исполнения и каждой заявке присваивается некоторый приоритетный индекс. Заявка с меньшим индексом имеет наибольший приоритет.

В теории массового обслуживания под временем обслуживания понимают время, которое затрачивается на обслуживание одной заявки конкретным обслуживающим прибором. В общем случае время обслуживания характеризуется определенным законом распределения

 

F(t) = P(t_обс < t),

 

где P(t_обс < t) – вероятность того, что время обслуживания t_обс < t.

При t_обс < 0 F(t) = 0. Время обслуживания реальной заявки на ЭВМ определяется числом операций, входящих в программу. Существенное влияние на это время оказывает разветвленность программы. Для слабо разветвленных программ число выполняемых операций практически для каждой задачи одинаково и может быть использована модель с постоянным временем обслуживания. при значительной разветвленности программы в зависимости от типа заявки ее реализация может пойти по разным направлениям, время выполнения программы будет случайной величиной, т.е. реализуется модель с переменным временем обслуживания. Поведение вычислительной системы во времени может быть описано на основе исследования марковского процесса.

 

Рассмотрим отдельные наиболее характерные модели обслуживания.

Экспоненциальный закон времени обслуживания простейшего потока заявок. Простейшим называют стационарный ординарный поток без последействия. Обозначим интенсивность заявок через l (l = const). Простейший поток описывается распределением Пуассона, в соответствии с которым вероятность возникновения k заявок за время t составляет

 

P(k, t) = (lt)^ke ^-lt/ k!.

Математическое ожидание числа заявок за время t определяется как

.

 

Соответственно дисперсия числа заявок за время t равна

 

.

 

Такая модель хорошо описывает многие потоки заявок вычислительных задач, которые возникают в реальных условиях эксплуатации.

 

Экспоненциальный закон времени обслуживания простейшего потока заявок при S обслуживающих приборах. В этом варианте обслуживания вычислительная система включает S обслуживающих приборов (ЭВМ) и имеет очередь для поступающих заявок с числом мест L. При наличии хотя бы одной свободной ЭВМ поступившая заявка сразу принимается на обслуживание. Если все ЭВМ заняты, то она становится в очередь. Естественной дисциплиной обслуживания является «первым пришел – первым обслужен». По числу заявок система может иметь состояния: «0, 1, …, S + L».

Вероятность нахождения вычислительной системы в k-ом состоянии

 

.

 

Соответственно вероятность состояния (S + n)

 

,

 

где вероятность отсутствия заявок в вычислительной системе

 

.

 

В приведенных формулах m = 1 / Т_обс – интенсивность обслуживания заявок; Т_обс - среднее время обслуживания одной заявки.

Вероятность потерь заявки (отказ в приеме на обслуживание возникает в случае, когда заняты все ЭВМ системы и в очереди находится L заявок) равна

 

Организация очереди в вычислительной системе требует знания ее средней длины. При условии, что очередь возникает, когда заняты все обслуживающие приборы и в системе имеет место количество заявок от S + 1 до S + L ее длина равна

 

.

 

При организации вычислительного процесса существенное значение имеет момент запуска и выпуска решаемой вычислительной задачи, поэтому весьма важно знать время пребывания заявки в очереди (время ожидания Т_ож). Среднее время ожидания

 

.

 

Конечные выражения для однолинейной системы с ограниченной очередью (при S = 1) имеют вид:

 

;

 

;

 

Среднее время пребывания заявки в вычислительной системе

 

.

 

Модель планирования вычислительного процесса

Для решения каждой задачи должен быть выделен определенный ресурс по объ­ему оперативной и внешней памяти, по времени работы процессора, времена ввода-вывода информации. Естественно, что ограничен­ность вычислительных ресурсов может не позволить решать вычис­лительные задачи параллельно во времени. Учитывая, что вычис­лительная система при однолинейном обслуживании зачастую мо­жет решать только одну задачу, необходимо составить план после­довательного запуска задач. Процесс назначения порядка решения задач во времени называется планированием. Для многолинейной системы планирование предполагает распределение заявок как во времени, так и в пространстве по используемым ЭВМ. В качестве распределяемых ресурсов выступают машинное время процессоров, объемы оперативной памяти и внешних запоминающих устройств, время работы устройств ввода-вывода. Эти ресурсы могут быть реализованы, если вычислительная задача подготовлена к выполне­нию ее вычислительной системой. Подготовка вычислительной за­дачи к исполнению осуществляется управляющей программой, на­зываемой планировщиком. Планировщик обеспечивает ввод вычис­лительных задач в вычислительную систему с предварительным формированием определенных информационно-вычислительных работ на базе заявок вычислительных задач. При возникновении заявки на решение вычислительной задачи необходимо установить программу и набор данных, которые позволят сформировать ин­формационно-вычислительную работу по решению данной задачи. Одновременно следует установить потребность в ресурсах и вклю­чить сформированную информационно-вычислительную работу в список работ, готовых для последующего исполнения. В резуль­тате планирования по каждой задаче может быть сформирован ряд работ, выполнение которых возможно при реализации управля­ющей программы, называемой супервизором.Супервизор обеспечи­вает предоставление каждой сформированной работе определен­ного ресурса процессора и других устройств вычислительной систе­мы. Супервизор действует по запросу, на который откликается программа управления работами и процессором. При управлении информационно-вычислительными работами супервизор непрерыв­но инициируется командами, которые задает планировщик. Плани­ровщик в соответствии с планом организации вычислительного процесса из множества заявок на решение вычислительных задач выделяет наиболее приоритетную и требует обеспечения ее соответ­ствующими ресурсами. Для этого он обращается к программе управления вводом и выводом, памятью и т. д. В целом функция планирования реализуется управляющими программами планиров­щика и супервизора. Критерии, используемые при планировании вычислительного процесса, могут выбираться в зависимости от требований к решаемым вычислительным задачам. Можно идти по пути уменьшения среднего времени решения задач в вычислитель­ной системе или увеличивать производительность. Возможны вари­анты, когда имеются ограничения на время решения конкретных задач, что особенно важно в системах управления в реальном масштабе времени.

Рассмотрим модель планирования вычислительного процесса. Будем считать, что в целом для ряда вычислительных задач необходимым является выполнение определенной номенклатуры типовых вычислительных работ J₁ - J_g , для которых необходимо предоставление ресурсов R₁ - R_n. Связь между работами и ре­сурсами можно установить в виде матрицы трудоемкости работ. Элементами этой матрицы служат параметры t_ij, которые в зависимости от характера требуемого ресурса имеют размерность числа единиц потребной памяти либо единиц времени, необхо­димых для выполнения соответствующей работы. Тогда вводимая матрица имеет вид

 

R₁ R₂ R_n

 

Имея данную матрицу, при составлении плана организации вычислительного процесса необходимо указать очередность выпол­нения работы отдельными устройствами вычислительной системы, т. е. последовательность использования ресурсов R₁ … R_n.

Планирование вычислительного процесса осуществляется с це­лью составления последовательности, т. е. расписания выполнения информационно-вычислительных работ, производимых при реше­нии поступивших вычислительных задач. Учитывая, что при реше­нии вычислительной задачи используются разные устройства вычи­слительной системы (ВС), можно рассмотреть два крайних случая:

1) порядок использования отдельных устройств ВС определяется поступившими вычислительными задачами;

2) порядок использова­ния устройств ВС либо неизвестен, либо неодинаков для различных информационно-вычислительных работ.

Этим крайним постанов­кам могут соответствовать и разные критерии эффективности со­ставления плана вычислительных работ. Для первой постановки в качестве критерия может быть выбран минимум суммарного времени решения вычислительных задач, для второй — можно из­брать в качестве критерия максимум загрузки устройств ВС. Плани­рование по минимуму суммарного времени решения вычислитель­ных задач возможно, если известна матрица трудоемкостей отдель­ных работ. Предполагая, что ресурсы вычислительной системы используются последовательно и выделяя типовую последователь­ность прохождения любой вычислительной задачи, можно получить эффективный алгоритм планирования на основе задачи Джонсона, которая относится к теории расписаний и широко используется в календарном планировании.

Планирование по критерию минимума времени обработки.

При планировании вычислительного процесса необходимо учитывать следующие ограничения:

1) для любого устройства ВС (фазы обработки данных) каждая последующая работа не может начаться до окончания предыдущей;

2) каждое устройство на данной фазе может выполнять только одну информационно-вычислительную работу;

3) начавшаяся информационно-вычислительная работа не долж­на прерываться до полного ее завершения.

Если в процессе обработки выделить n фаз, на каждой из кото­рых используется одно вычислительное устройство, то решение данной задачи путем перебора требует рассмотрения (N!) вариан­тов, где N — число заявок на решение вычислительных задач в вы­числительной системе. Джонсоном получен эффективный алгоритм для n = 2, требующий перебора N(N+1)/2 вариантов. Частное реше­ние задачи Джонсона соответствует случаю n = l. По сути, это однолинейная система обслуживания (S = 1), в которой имеется очередь заявок. Требуется установить порядок выборки этих заявок диспетчером Д задач для обработки в ЭВМ. Критерием может быть минимум времени пребывания заявки в вычислительной системе, включая и время ожидания ее в очереди. Алгоритм выборки заявок из очереди по данному критерию соответствует их расположению в порядке убывания времени пребывания в вычислительной системе. Отметим, что решение задачи Джонсона при n = l имеет слабое практическое применение для вычислительной системы. Обычно при обработке данных используется более одного устройства, по­этому рассмотрим эту задачу для n = 2.

Пусть известна матрица Ттрудоемкостей выполнения работ при решении вычислительных задач. Эта матрица содержит gстрок, отображающих работы J₁, J₂, …, J_g и n столбцов, соответствующих используемым вычислительным устройствам. Как принято выше, v = 2, тогда элементами матрицы будут трудоемкости t₁₁, t₂₁, ..., t_g1 – выполнения работ первым вычислительным устройством и t₁₂, t₂₂, ..., t_g2– выполнения работ вторым вычислительным устройством. Требуется по критерию минимума суммарного времени выполнения информационно-вычислительных работ упорядочить их в очереди. Решение задачи Джонсона предполагает следующий алгоритм оптимального планирования:

1) в матрице трудоемкостей определяется min (t₁₁, t₁₂, ..., t_g2);

2) выбираются работы J₁, J₂, …, J_g , для которых трудоемкости соответствуют минимальному времени, хотя бы для одного вычислительного устройства, то есть t_ij = t_min;

3) работы разделяются по минимальному времени их исполнения на первом и втором вычислительных устройствах, то есть выделяются t_it_min, t_mint_j;

4) в начало очереди включаются работы с трудоемкостью t_mint_j, в конец очереди включаются работы с трудоемкостью t_it_min;

5) вставленные в очередь работы исключаются из матрицы трудоемкостей и строится новая матрица по оставшемуся числу работ;

6) для построенной матрицы выявляется новая минимальная трудоемкость. В соответствии с рассмотренным алгоритмом работы из данной матрицы располагаются в требуемой последовательности в средней части образованной ранее очереди.

 

Планирование по критерию максимума загрузки средств обработ­ки.

Если последовательность использования вычислительных устройств в системе при решении задач неизвестна, то планирование ведут на основе критерия максимальной загрузки устройств. В этом случае из J₁, J₂, …, J_g отбирается совокупность работ, которые могут выполняться совместно на базе имеющихся ресурсов. По мере окончания хотя бы одной работы из этой совокупности выполнения заменяется одной из работ, находящихся в ожидании.

Для определе­ния составов совокупностей работ преобразуем матрицу трудоем­костей в матрицу загрузки устройств. Введенные ранее ресурсы R₁ … R_n принадлежат некоторым устройствам У₁ ...У_n. Тогда матрица загрузки может быть представлена в виде

У₁ У₂ У_n

 

где элемент матрицы 3_ij показывает загрузку j-го устройства i-й работой; , i = 1, 2, ..., g, t_ij – потребность i-й работы в использовании j-го ресурса.

В каждой строке матрицы выделим элемент 3_ij с наибольшим значением. Тогда значение jопределит номер потока, к которому будет отнесена работа, соответствующая данной строке матрицы. Число потоков будет равно числу устройств, т. е. n. Если в первой строке наибольшее значение имеет элемент З₁₂, то работу J₁относим к потоку П₂. Соответственно если во второй строке наибольшее значение имеет элемент 3_2n, то работу J₂ относим к потоку П_n. При разбиении работ на потоки примем ограничение, что каждая из них может быть отнесена только к одному потоку. Каждый поток включает тогда некоторую последовательность работ. Сформиро­вав n потоков, можно перейти к составлению совокупностей работ. Совокупности работ, поступающих на обработку, образуются пу­тем выборки их из потоков П₁ ... П_n. В начальный момент времени формируется первая совокупность, включающая n работ, взятых по одной из каждого потока. Эти работы поступают на соответст­вующие устройства при условии, что они не перегружают некото­рый общий ресурс. В качестве такого ресурса может выступать емкость оперативной памяти, поэтому для каждого момента форм­ирования совокупности работ должно соблюдаться ограничение: сумма емкостей памяти, занимаемых работами, включенными в со­вокупность, не должна превышать общей емкости памяти. Пусть в начальный момент совокупность работ имеет вид C₁ = {J₃, J₁, …, J₂}. Эта совокупность содержит n членов, из которых, как раньше приняли, работа J₁ принадлежит потоку П₂, а работа J₂ принад­лежит потоку П_n. Ограничение по оперативной памяти примет вид V₃ + V₁ + … + V_i + … + V₂ £ V, где V — общий объем оперативной памяти; V_i - объем оперативной памяти, необходимый для работы i.

Если в некоторый момент времени завершается работа J₁, то на ее место в совокупность работ включается следующая работа из того же потока П₂. При этом опять проверяется ограничение. Если оно не соблюдается, то выбирается следующая работа из данного потока. При отсутствии работ, соответствующих огра­ничению, может быть выбрана новая из другого потока.

Рассмотренные варианты планирования вычислительных работ при решении вычислительных задач являются классическими. Разработано большое число методов планирования, которые базиру­ются на теории расписаний. Принципы планирования работ широко используются в типовых операционных системах современных ЭВМ.

Вычислительный граф системы обработки.

Реальный вычислительный процесс состоит из работ. Каждая работа реализуется на основе программы при наличии соответствующих данных. В процессе выполнения работы осуществляется обработка имеющегося набора данных. Перечень работ, возникающих при решении вычислительной задачи, определяется ее алгоритмом. На логическом уровне алгоритм решения задачи может быть представлен граф-схемой, приведенной на рис. 5, вершины которой отображают отдельные процедуры. Дуги граф-схемы алгоритма — это отношения, т. е. связи между процедурами в алгоритме. Обычно процедуры реализуются на основе стандартного программного обеспечения. По своему содержанию процедуры могут соответствовать рассмотренным выше информационно-вычислительным работам. Так же как и работы, они выполняются параллельно-последовательно во времени, поэтому в корне графа располагается некоторая начальная (головная) процедура Р₀,а в зависимых вершинах — процедур
ы Р₁, Р₂, Р_n. При наличии головной вершины граф имеет древовидную структуру. Дуге графа может быть приписан вес p_ji, отражающий число вызовов процедуры Р_i, при однократном выполнении предшествующей процедуры P_j.

Рис. 5

 

Если алгоритм имеет детерминированный характер, то p_ji = 1;для вероятностного алгоритма возникает условный переход, тогда p_jiотображает вероятность перехода по данной дуге, т. е. p_ji < 1;в случае итеративного перехода p_ji > 1. Совокупность алгоритмов обработки данных составляет алгоритмическую модель системы обработки.