ксидные расплавы и их термодинамические характеристики.

екция №8

ФИЗИКО-ХИМИЧЕСКАЯ ХАРАКТЕРИСТИКА СТАЛЕПЛАВИЛЬНЫХ ПРОЦЕССОВ. Оксидные расплавы и их термодинамические характеристики. Расчет активностей компонентов шлакового расплава по молекулярной теории расплавленных шлаков, по теории совершенного ионного раствора, по теории регулярных ионных растворов, а также как фазы, имеющей коллективную электронную систему

ксидные расплавы и их термодинамические характеристики.

Шлаки выполняют важные и разнообразные функции в высокотемпературных металлургических процессах. Управление процессами окисления и восстановления различных элементов металлического расплава, удаление вредных примесей (серы, фосфора и др.) из расплавленного металла и другими процессами в значительной мере основано на изменении состава и физико-химических свойств расплавленного шлака.

Под шлаком понимают расплав различных оксидов. В составе шлака могут быть также в небольшом количестве сульфиды и фториды.

Металлургические шлаки имеют в своем составе следующие оксиды: FeO, MnO, CaO, MgO, SiO₂, Cr₂O₃, Al₂O₃, TiO₂, V₂O₅, P₂O₅.

Расчет активностей компонентов расплавленного шлака производят на основе двух модельных представлений о строении шлакового расплава, получивших название молекулярной (или химической) и ионной теории расплавленных шлаков.

Согласно молекулярной теории шлак состоит из молекул свободных оксидов и соединений между оксидами с различной химической природой (силикаты, ферриты, фосфаты). Химические соединения частично диссоциированы. В реакциях с металлом принимают участие только свободные оксиды. Поэтому мольная доля свободных оксидов принимается равной активности этих оксидов в шлаковом расплаве. Методика расчета концентраций свободных оксидов по общему составу шлака была разработана Г. Шенком. В дальнейшем методику расчета концентраций свободных оксидов усовершенствовали путем формального допущения о существовании в шлаковом расплаве молекул сдвоенных силикатов. Такое допущение давало лучшую сходимость с экспериментальными данными, но не имело теоретической или экспериментальной основы.

Более обоснованной является ионная теория строения расплавленных шлаков, в соответствии с которой шлак в расплавленном состоянии представляет собой ионный раствор.

В качестве стандартного состояния для отдельных компонентов шлакового расплава чаще всего принимают чистые оксиды. Поэтому учет реальных взаимодействий между частицами, сводится обычно к определению активности или коэффициента активности того или иного оксида, входящего в состав шлака.

Расплавленные шлаки представляют собой реальные растворы, показывающие значительные отклонения от идеального поведения.

Поэтому для количественных расчетов равновесий с участием расплавленных шлаков нужно знать активность данного компонента шлакового расплава, которая связана с его концентрацией в шлаке соотношением:

а_МеО=g_МеОх_МеО, (2.1)

где g_МеО – коэффициент активности оксида МеО в расплавленном шлаке по отношению к стандартному состоянию чистого оксида; х_МеО – мольная доля оксида МеО в шлаковом расплаве.

Зная состав шлака, который обычно выражают в процентах по массе, определяют расчетным путем мольные доли компонентов. Затем определяют коэффициент активности оксида в шлаковом расплаве и находят величину –активности соответствующего компонента.

Расчет активностей компонентов шлакового расплава

по молекулярной теории расплавленных шлаков

Согласно молекулярной теории расплавленных шлаков, активная концентрация (или активность) компонентов равна концентрациям свободных оксидов в расплаве. Сам расплав рассматривается как идеальный раствор свободных оксидов и молекул химических соединений, образовавшихся из оксидов с различной природой, например силикатов СаО*SiO₂, 2FeO*SiO₂, 2MnO*SiO₂, феррита 3СаО*Fe₂O₃, фосфата 4СаО*Р₂О₅. Принимают, что отдельные соединения частично диссоциированы, и в расчет вводят константу их диссоциации. Существует несколько методов расчета концентрации свободных оксидов в шлаковом расплаве. Они отличаются выбором соединений между компонентами шлака. Соотношения между свободными оксидами и химическими соединениями устанавливают на основе материального баланса и степени диссоциации соединений, принятых в расчете.

Винклер и Чипман предложили способ расчета активностей FеО и СаО в основном семикомпонентном шлаке, в котором число молей отдельных оксидов обозначается символом n и соответствующим индексом:

FeO – n₁, MnO – n₂, CaO – n₃, MgO – n₄, SiO₂ – n₅, Fe₂O₃ – n₆, P₂O₅ – n₇

В шлаках нет Al₂O₃ и СаF_2.

Принимается существование в расплаве следующих соединений: 4СаО*2SiO_2, СаО*Fe₂O₃, 4СаО*Р₂О₅. Делается допущение, что весь кремнезем связан в силикаты кальция, а , Fe₂O₃ – в феррит кальция. Тогда число молей соединений будет связано с числом молей отдельных оксидов в шлаке соотношениями: n_4CaO*2SiO2 = 1/2n₅; n_CaO*Fe2O3 = n₆; n_4CaO*P2O5 = n₇.

При расчете числа молей свободной СаО все основные оксиды (СаО, МgO, MnO) суммируются и рассматриваются как СаО. Число молей свободной СаО в таком случае:

n_CaO,своб = n₂ + n₃ + n₄ – 2n₅ – n₆ –4n₇. (2.2)

Общее число молей всех структурных составляющих шлака:

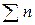= n₁ + n_CaO,своб + n_4CaO*2SiO2 + n_CaO*Fe2O3 + n_4CaO*P2O5 =

=n₁+n₂+n₃+n₄–3/2n₅–3n₇ (2.3)

Активность СаО и FeO соответственно:

а_СаО = n_CaO,своб/ 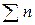; (2.4)

a_FeO = n₁/ 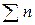. (2.5)

Допущение о частичной диссоциации сложного силиката по реакции:

(4СаО*2SiO₂) = (2СаО*2SiO₂) + = (2СаО)_своб

приводит к более сложным расчетам при определении n_CaO,своб и .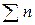

 

Расчет активностей компонентов шлакового расплава по теории

совершенного ионного раствора

Эта модель была разработана М.И.Темкиным. Модель предполагает, что расплавленный шлак состоит только из ионов, а ближайшими соседями являются ионы разного знака. Одноименно заряженные ионы равноценны в отношении их взаимодействия с соседями и различаются только по зарядам. Теплота смешения при образовании раствора принимается равной нулю. Изменение энтропии равно сумме энтропий смешения, вычисленных отдельно для катионной и анионной части расплава.

В совершенном ионном растворе, как было показано М.И.Темкиным, активность компонента равна произведению ионных долей тех ионов, из которых состоит данный компонент.

Например:

Ионные доли рассчитывают отдельно для катионной и анионной частей раствора, т.е. число грамм-ионов того же знака:

(2.6)

Если обозначить число молей каждого оксида, входящего в состав шлака через n_МеО, то для основных оксидов принимается их диссоциация по реакциям:

СаО=Са²⁺+О^2-; MgO=Mg²⁺+O^2-; FeO=Fe²⁺+O^2-.

Тогда для катионов:

Общее число грамм-ионов катионов:

(2.7)

Кислотные и амфотерные оксиды образуют комплексные анионы:

Тогда для сложных анионов:

и т.д.

Поставщиками анионов кислорода являются основные оксиды. Вместе с тем значительное число анионов кислорода расходуется на образование комплексных анионов. Поэтому число свободных грамм-ионов кислорода в расплаве определяется разностью общего числа грамм-ионов кислорода, равного числу молей основных оксидов и числом грамм-ионов кислорода, израсходованных на образование комплексных анионов.

= (2.8)

Общее число грамм-ионов анионов:

= (2.9)

 

Расчет активностей компонентов шлакового расплава по теории регулярных ионных растворов

В.А.Кожеуровым разработана статистическая теория ионных растворов, основные положения которой включают предположения о полной диссоциации компонентов шлака на одноатомные ионы. Расплавленный шлак рассматривается как система, состоящая из отдельных не кислородных одноатомных частиц катионов, которые окружены анионами кислорода. Между катионами и анионами действуют силы межчастичного взаимодействия. Используя уравнения статистической термодинамики для ионных растворов, для системы из k компонентов получено уравнение для определения активности любого из них при наличии других составляющих с ионной долей x_i:

(2.10)

где Q_il, Q_li, Q_ij – энергия смешения соответствующих компонентов.

Значения энергий смешения можно определить из двойных диаграмм состояния соответствующих компонентов или по экспериментальным данным. Принимают, что: Q_il=Q_li. Значения Q_ij находят для различных пар компонентов шлака.

В.А.Кожеуровым уравнение (2.10) было обобщено для шлаков сложного состава с учетом экспериментальных значений теплот смешения отдельных компонентов. Шлак рассматривается как шестикомпонентная система. Обозначим ионные доли катионов:

Fe – x_Fe Mn – x_Mn Ca – x_Ca Mg – x_Mg Si – x_Si P – x_p

Ионные доли катионов рассчитываются так же, как по теории совершенных ионных растворов:

(2.11)

где х_i–ионная доля катионов; –число частиц не кислородного элемента в молекуле оксида, из которой образуется данный катион (для СаО =1, для Р₂О₅ =2); n_i–число молей данного оксида в 100 г шлака; k–число компонентов шлака. Приняв известные величины смешения для различных пар компонентов и значения ионных долей катионов для заданного шлака, В.А.Кожеуров получил уравнения для расчета коэффициентов активностей оксидов, из которых образован данный шлак:

(2.12)

(2.13,2.14)

(2.15)

Уравнение (2.15) для lg выведено для случая, когда х_Р=0.

Все выведенные уравнения (2.12)–(2.15) относятся к сильно основным шлакам. Они достаточно хорошо согласуются с экспериментальными данными. Поскольку сделано допущение о существовании в шлаковом расплаве анионов только одного сорта (О^2–), ионная доля анионов кислорода будет равна единице.

Активности компонентов шлака рассчитываются так же, как для совершенного ионного раствора, т.е. как произведение ионных долей катионов и анионов, но дополнительно вводится значение коэффициента активности соответствующего катиона:

Для компонента Р₂О₅, который образует два катиона, активность:

(2.19)

 

Расчет активностей компонентов шлака как фазы, имеющей коллективную электронную систему

Методика расчета разработана А.Г.Пономаренко. В соответствии с теорией расплавленного шлака как фазы имеющей коллективную электронную структуру, компонентами шлаковой фазы являются химические элементы. Электроны всех атомов, образующих расплавленный шлак, составляют единую квантово-механическую систему, которую термодинамически можно характеризовать химическим потенциалом электронов. Это позволяет представить парциальную энтропию смешения в виду двух составляющих, учитывающих тепловое возбуждение ядер и электронов отдельно.

Парциальная энтропия смешения, как и в теории совершенных ионных растворов, принимается равной нулю.

В соответствии с принятыми условиями получено выражение для химического потенциала элемента i в шлаке:

(2.20)

где – стандартный химический потенциал элемента i в шлаковой фазе; –химический потенциал электронов; –валентность элемента i в оксидной фазе; –активность компонента i в оксидной фазе.

Рассматривая равновесие в системе шлак-металл, можно исключить неизвестную величину и учесть отклонение от идеального поведения, используя значение энергий взаимодействия компонентов, составляющих шлаковый расплав.

Разработанная модель этого метода позволяет рассчитать активности компонентов шлака как химических элементов, используя так называемые атомные коэффициенты активности:

a_(i)=C_(i) , (2.21)

где C_(i)–концентрация элемента i в шлаке, выраженная в атомных долях; –атомный коэффициент активности элемента i.

Для определения значений используется уравнение:

(2.22)

где k–полное число компонентов шлака (число сортов атомов); j–любой компонент шлака; –энергия обмена компонентов i и j.

Расчет значений производится по уравнению:

À À )², (2.23)

где À_i, À_j–атомные параметры элементов i и j.

Численное значение атомных параметров для различных элементов по данным А.Г.Пономаренко приведено в таблице 2.

 

Приложение 6. Атомные параметры элементов.

Элемент,i	Валентность,	À, кДж	Элемент,i	Валентность,	À, кДж
Fe		334,7	Si		171,5
Mn			Mg		146,4
O	–2		P
Ca		194,6	Al
Cr			S	–2

 

Активность компонентов шлака как оксидов определяется по обычному соотношению:

(2.24)

В связи с большим различием в атомных параметрах кислорода и катионных компонентов шлака значение практически равно единице и активность оксида в шлаке :

. (2.25)