ЛОКАЛИЗАЦИЯ ТОЧКИ НА ШКАЛЕ 2 страница

Получив возможность расположить стимулы по субъективной шкале красоты, можно перейти к обратной процедуре — выявить, какой физический параметр в стимулах меняется в соответствии с полученной шкалой, и проверить, можно ли интерпретировать этот параметр как физический коррелят красоты.

§ 5. Многомерный анализ сложных стимулов

Однако модель Терстоуна предполагает обязательную одномерность шкалируемого свойства объектов, в данном случае “красоты” цветных карт, т.е., независимо от того, сколько физических характеристик стимула определяет оценку “красоты” цвета, психологически все карты должны быть выстроены в некоторую последовательность по степени красоты. Если же в действительности для оценки красоты цвета используется больше, чем одна субъективная размерность (как, например, при оценке различий между аппертурными цветами: одна — для цветового тона, другая — для насыщенности), то, используя модель Терстоуна, построить адекватную шкалу “красоты” цвета невозможно. В лучшем случае это будет какая-то проекция действительных шкал в одномерное пространство, на одну шкалу, и восстановить эти исходные шкалы по имеющейся единственной шкале, конечно, невозможно.

Естественно, что в этом случае невозможно решить и главную задачу, т.е. построить психофизическую функцию, поскольку невозможно обнаружить те физические свойства стимула, которые объясняют субъективные оценки.

Задачи построения сложных “многомерных” субъективных шкал и их последующей связи со шкалами физических свойств стимуляции породили целый ряд методов так называемого многомерного анализа (факторный анализ, многомерное шкалирование, дискриминантный и кластерный анализ).

В общем виде схему применения этих методов можно проиллюстрировать на одном из наиболее распространенных методов такого типа — на факторном анализе. Основная гипотеза факторного анализа заключается в том, что каждый объект-стимул можно описать как линейную комбинацию небольшого числа основных факторов. Число и характер этих факторов определяют априорно выделенные “существенные” параметры объектов. На основе измерений выделенных характеристик объектов строятся корреляционные или ковариационные матрицы, анализ которых приводит к локализации стимулов в пространстве основных факторов, которые интерпретируются как субъективные шкалы. Каждую субъективную шкалу соотносят с физическими параметрами стимула, выявляя связь по типу одномерной психофизической функции. В случае обнаружения однозначной связи между субъективными измерениями и физической переменной, задачу можно считать решенной. Любой новый стимул будет расположен на субъективной шкале просто путем вычислений по результатам физических измерений.

Но перенос этого принципа на субъективное шкалирование сложных стимулов порождает новую проблему. Даже в случае, когда для сложного стимула известны физические параметры, с которыми связано изменение субъективных оценок, совсем не так просто установить однозначную связь между стимулом и реакцией. Например, восприятие аппертурных цветов традиционно определяется такими субъективными характеристиками, как цветовой тон, насыщенность и яркость. Известны и определяющие их физические параметры: длина волны светового излучения, спектральный состав излучения (чистота) и его интенсивность. Казалось бы, достаточно иметь три одномерные функции типа R=f(S), чтобы описать ощущение такого сложного стимула, как цвет. Но все оказывается значительно сложнее, поскольку изменение длины волны излучения приводит к изменению не только цветового тона, но одновременно меняется и другая субъективная характеристика — насыщенность, например. Или изменение интенсивности светового излучения приводит к изменению яркости, но вместе с тем меняется и ощущение цветового тона, хотя длина волны излучения не меняется, и т.д. Таким образом, простой набор одномерных психофизических функций не гарантирует описания субъективного изменения многомерного стимула.

§ 6. Многомерное шкалирование

 

Приведенный пример с цветовыми стимулами, когда непосредственные физические измерения не объясняют однозначно субъективных шкал, является наиболее типичным случаем (и наиболее интересным); именно в этом случае и применяются разрабатываемые в последние годы новые методы измерения, называемые многомерным шкалированием (Торгерсон, 1958; Шепард, 1962; Крускэл, 1964).

Ясно, что когда люди оценивают сложное качественное свойство объектов, такое как эмоциональное выражение лица, или когда они оценивают общее сходство сложных объектов, они ведут себя так, как если бы мерили объекты сразу по нескольким субъективным шкалам, а не по одной. Комбинируя определенным образом субъективные меры, они и осуществляют сложное суждение, подобное оценке психологического качества. Иначе говоря, сложную субъективную шкалу можно представить как систему нескольких простых субъективных шкал. Тот факт, что люди используют для объяснения некоторого качества зачастую более чем одну физическую шкалу, наводит на мысль, что субъективные шкалы также могут быть составными. Можно представить себе далее, что свои измерения по субъективным шкалам люди осуществляют какими-то не всегда осознанными методами комбинирования характеристик объектов. Поэтому вполне вероятно, что некоторые из этих субъективных шкал не соответствуют однозначно простым физическим шкалам. Применение методов одномерного шкалирования, описанных выше, оставляет мало надежды получить полезную информацию об этих “составных” шкалах.

В конечном итоге становится очевидным, что модель, которая походит на многомерные модели в том, что может трактоваться как система шкал, и которая не требует, чтобы эти шкалы определялись заранее до анализа данных (как, например, в случае с факторным анализом), будет обладать большой ценностью. Подобная модель может применяться непосредственно к оценочным данным, чтобы получить основные субъективные шкалы безотносительно к любым предположениям о физических коррелятах этих шкал.

Для решения таких проблем и развивались методы многомерного шкалирования. При использовании этих методов предполагается, что в основе сложных суждений человека лежит система из нескольких субъективных шкал, которая и формирует субъективное пространство. Когда испытуемых просят сравнить пару объектов, они ориентируются на различия между объектами по каждой субъективной шкале, и итоговая оценка различия есть величина, производная от различий по каждой шкале. В качестве модели системы субъективных шкал обычно используется геометрическое пространство, точки которого представляют исходные стимулы. Оси геометрического пространства интерпретируются как субъективные шкалы, а шкальные величины каждого стимула — как значения координат соответствующей точки. Предполагается, что если стимулы представить как точки пространства, то субъективные оценки различий определенным образом соотносимы с расстояниями между точками в субъективном пространстве. Конкретный вид связи между субъективными различиями и межточечными расстояниями в каждом случае может быть различным. Он определяется используемой моделью субъективного расстояния, но в данном случае понятно, что два стимула, сильно различающиеся между собой, будут расположены на далеком расстоянии друг от друга в пространстве, а сходные стимулы расположатся рядом.

В примере, который приводился, субъектам предлагали оценивать пары цветовых карт по заданному качеству (красоте). В случае многомерного шкалирования от субъекта требуется аналогичная оценка, но не самого отдельного признака, а оценки степени общего сходства или различия между парами стимулов, по которым строится шкала межстимульных различий. Результаты подобных измерений содержат в себе всю информацию о структуре множества стимульных точек в субъективном пространстве. Вопрос заключается в том, как ее оттуда извлечь?

Рассмотрим гипотетический пример многомерного шкалирования цветоразличения. Предположим, что мы предъявили испытуемому три цветные карты (А, В и С). Карта А окрашена в белый цвет, карта С — в желтый и карта В — в оранжевый.

Оценки различий, которые произвел испытуемый для всех карт, следующие:

 

 

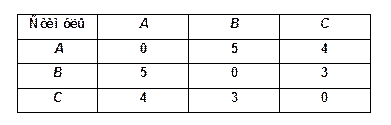Возьмем в качестве модели субъективного расстояния евклидову метрику и допустим, что оценки различий связаны с расстояниями в евклидовом пространстве прямой пропорциональностью. Если данные оценки действительно основаны на одномерной шкале, мы должны расположить точки, представляющие наши цветные карты, вдоль одной оси так, чтобы расстояние между точками соответствовало оценкам различий. Это значит, что, памятуя о предположении, что оценки различий прямо соотносимы с расстояниями в субъективном пространстве, расстояние между какими-то двумя точками должно равняться сумме расстояний от этих точек до третьей. Но для данных вышеприведенной таблицы это следствие никак не может быть выполнено. Из этого следует, что три данных цвета нельзя расположить на одномерной шкале. Поскольку стимулов всего три, то они располагаются, как минимум, в двухмерном пространстве (рис.1), иначе говоря, оцениваются по двум шкалам. Определяя минимальную размерность пространства, которая снимает несовместимость полученных оценок, метод многомерного шкалирования позволяет обнаружить число необходимых субъективных шкал, лежащих в основе сложных суждений.

Полученные две оси субъективного пространства легко интерпретировать как две субъективные характеристики цветовых стимулов: шкалу цветового тона и шкалу цветовой насыщенности. Эта интерпретация наглядно следует из структуры цветовых точек в пространстве (рис. 1), построенном по данным этой таблицы. В соответствии с такой интерпретацией можно выбрать систему ортогональных координат и вычислить проекции точек на оси. Эти значения будут прямо соответствовать шкальным значениям цветового тона и насыщенности анализируемых стимулов.

Конечно, в подобном случае перед исследователями остается проблема физической интерпретации этих субъективных шкал, и хотя многомерное шкалирование не предлагает однозначного решения этой проблемы, но оно все-таки является более полезным, чем процедура одномерного шкалирования. Прежде всего, определяя действительные субъективные шкалы, которые субъекты используют для оценивания объектов, а не априорный набор шкал, метод многомерного шкалирования дает исследователю больше шансов выявить физические свойства объектов, которые человек реально использует как основу для субъективных измерений. Другими словами, отношение между каждой субъективной и физической шкалой может быть определено раздельно. Кроме этого, явно определяя субъективные шкалы (даже если соответствующие физические шкалы неизвестны), эти процедуры дают полезную информацию о том, какие физические измерения необходимо сделать, чтобы попытаться найти физический коррелят субъективной шкалы. И последнее, вся эта информация получается без обращения к традиционным методам шкалирования — более сложным и трудоемким.

Важное значение по отношению к задачам прикладного характера имеют особенности многомерного шкалирования, связанные с выявлением не только структуры субъективного пространства стимулов, но и возможностей определения тонких индивидуальных различий между самими испытуемыми (Клифф, 1973; Терехина, 1975; Виш и Кэрролл, 1974).

Рассмотрим это на примере тех же цветовых карт. Допустим, что оценивая различия между картами, одни испытуемые будут больше ориентироваться на различия по цветовому тону (рис. 2), другие — по насыщенности (рис. 3), а третьи — одинаково на те и на другие (рис.1).

Если все три группы испытуемых расположить в двумерном пространстве цветовой тон — насыщенность, мы получим следующую картину (рис. 4).

 

 

 

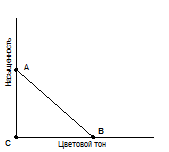Рис.1. Гипотетический пример расположения трех цветов (А, В и С) в двуxмерном евклидовом пространстве

 

Испытуемые группы 3 придают большое значение различиям в цветовой насыщенности, испытуемые группы 1 — различиям в цветовом тоне и игнорируют различия в насыщенности. Испытуемые 2 группы занимают среднее положение. Легко представить, что между этими группами возможны промежуточные варианты, и в таком случае можно использовать, например, угол наклона луча, проходящего из точки пересечения осей через данный класс испытуемых, как некоторую основу для классификации испытуемых (рис. 4). Измеряя этот угол относительно оси цветового тона, мы сможем разделить группы испытуемых по их предрасположению к цветовому тону или насыщенности.

 

 

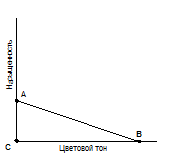Рис. 2. Гипотетический пример субъективного пространства восприятия трех цветов (А, В и С) испытуемыми, больше ориентирующимися при различении цветов на цветовой тон

 

 

 

Рис. 3. Гипотетический пример субъективного пространства восприятия трех цветов (А, В и С) испытуемыми, больше ориентирующимися при различении цветов на насыщенность

 

Естественно, что этот пример, как и все предыдущие, в значительной степени упрощен и схематизирован. Это сделано для того, чтобы подчеркнуть суть данной методики в применении к анализу индивидуальных различий, когда модель многомерного шкалирования предназначена не только для определения субъективных признаков, лежащих в основе суждений, но и для выделения более значащего из этих признаков, вносящего наибольший вклад в индивидуальные суждения.

Изложение сложных вопросов в простой и краткой форме неизбежно связано с разрывами в логической структуре. Этот недостаток будет компенсирован в следующих разделах при более детальном и строгом изложении моделей и процедур шкалирования. Однако более общий взгляд на исследуемый предмет обладает преимуществом охвата одновременно всех главных частей и связей, как это делает крупномасштабная карта. Чтобы еще раз подчеркнуть взаимосвязь различных методов шкалирования, подытожим в виде отдельных пунктов главные моменты излагаемого предмета:

 

 

Рис. 4. Пространство индивидуальных различий трех групп испытуемых

 

1. Психофизические измерения начинались с построения одномерных субъективных шкал (процедуры субъективного шкалирования Фехнера и Стивенса). Необходимым условием для осуществления субъективных измерений было наличие соответствующей физической шкалы. Физические измерения служили основанием и критерием истинности для субъективных измерений. В то же время применение этих моделей было чрезвычайно ограничено этим условием.

2. Принципиально новым шагом в психофизике явилась разработка методов субъективных измерений, не требующих предварительного построения физической шкалы стимула (модель шкалирования Терстоуна). Эти методы значительно расширили сферу применения субъективных измерений, включив в нее шкалы, не имеющие явных физических коррелятов. Существенным ограничением этих методов является обязательная одномерность измеряемой субъективной характеристики стимула.

3. Последующее развитие методов шкалирования связано с построением сложных многомерных шкал. Но практический прогресс соединялся в данном случае с методическим отступлением. В основание многомерных субъективных шкал вновь кладутся определенные характеристики объекта, которые должны быть заданы априорно, т.е. еще перед началом исследования (модели факторного анализа и др.).

4. Наконец, свою наиболее развитую форму психофизические измерения получили в моделях многомерного шкалирования, когда производимый анализ многомерных реакций на сложные стимулы не связан с предварительным физическим анализом стимуляции, а ориентирован исключительно на внутреннюю структуру суждений.

 

ЧАСТЬ I

ЛОКАЛИЗАЦИЯ ТОЧКИ НА ШКАЛЕ

(НОЛЬМЕРНОЕ ШКАЛИРОВАНИЕ)

Глава 1. МЕТОДЫ ИЗМЕРЕНИЯ ПОРОГОВ

Исторически сложилось так, что первыми методами психологических измерений были методы, позволяющие определять локализацию точки на психологической шкале. Их появлением мы обязаны Г. Т. Фехнеру, пытавшемуся с их помощью разрешить психофизическую проблему — выяснить закон соответствия психического образа и вызвавшего его физического воздействия. Согласно Фехнеру, через абсолютный порог задается начальная точка отсчета на психологической шкале, а через разностный порог вводится единица измерения на ней.

Под порогом всегда подразумевается некое критическое значение, разделяющее исследуемый ряд явлений на 2 класса. Абсолютный порог — то минимальное значение в континууме стимулов, выше которого раздражитель всегда воспринимается. Разностный порог — то минимальное различие в выраженности определенного физического параметра стимулов, превышение которого приводит к восприятию их различия.

Для решения основной задачи Фехнером была предпринята разработка методов измерения порога. Предложенные им три метода измерения порога добрую сотню лет были единственными методами определения чувствительности и до сих пор признаются классическими. Знакомство с ними и в наши дни составляет основу подготовки психолога-экспериментатора. И дело не только и даже не столько в том, что порог как мера чувствительности — психической способности воспринимать, чувствовать, реагировать — широко используется в различных областях психологических исследований. Главное в другом. Хотя пороговые, как и любые другие психофизические измерения, если их рассматривать в содержательном аспекте, представляют собой частный случай психометрических измерений, в пороговых методах — наиболее простых измерительных процедурах — уже нашли отражение основные трудности количественного определения переменных и способы их преодоления: вариабельность измеряемых величин и использование средних значений для их характеристики; их вероятностный характер, влияние многочисленных и далеко не всегда контролируемых экспериментатором факторов и введение уравновешивающих их действие процедур. Оба указанные качества — простота и характерность — определяют место пороговых методов в курсе обучения методам психологических измерений.

Развитие методов в науке обычно связано с появлением новых проблем. Главной и единственной задачей классической психофизики было изучение закона соответствия между психическими и физическими переменными. Основное внимание уделялось стимульным переменным, поскольку молчаливо предполагалось отсутствие влияния на ответы испытуемого в эксперименте таких несенсорных факторов как изменение мотивации, получение дополнительной информации об экспериментальной ситуации и т.д. Эти предположения реализовались в процедурных особенностях пороговых измерений и представлениях о пороге как мере чувствительности. Характерной чертой трех классических пороговых методов является довольно большое разнообразие стимулов, применяемых в эксперименте в качестве независимой переменной, и отсутствие какого бы то ни было контроля упомянутых выше несенсорных факторов, фактически всегда включенных в эксперимент. Те статистические показатели, которые приняты в этих методах в качестве пороговых мер, на самом деле являются, строго говоря, мерами исполнения, т.к. определяются не только уровнем чувствительности испытуемого, но и теми несенсорными факторами, которые управляют выбором его ответа. Несмотря на это, такие качества пороговых методов, как простота, меньшие затраты времени на измерение, а также удобство выражения пороговых мер в физических единицах обеспечивают этим методам широкое применение в современной исследовательской практике.

Современная психофизика (в отличие от классической), решая проблему измерения чувствительности, основное внимание уделяет процессу решения снсорной задачи (выбора испытуемым ответа) в типичной для порогового эксперимента ситуации отсутствия ясных отчетливых впечатлений от действия стимула. Это и определило характерные черты нового класса методов, детальная разработка которых осуществлена в последнее тридцатилетие — методов обнаружимости сигнала. Общим для всех методов этого класса является резкое обеднение стимульной ситуации (сведение ее всего до двух стимулов) и варьирование в качестве независимой переменной факторов, управляющих выбором ответа испытуемого. Описанию этих методов посвящена глава 2 данного раздела.

 

§ 1. Метод минимальных изменений

 

Данный метод является единственным среди методов измерения чувствительности, который дает знание величины порога в ходе самого измерения. В процедуре этого метода прямо отразилось понимание порога как барьера, разделяющего стимульный ряд на два класса ощущаемых и неощущаемых стимулов или их разностей.

 

1. Измерение абсолютного порога (RL) методом минимальных изменений.

Процедура. Существует несколько вариантов процедуры измерения этим методом. Рассмотрим процедуру Вундта. Каждая проба начинается сигналом “Внимание”, после которого с постоянным интервалом (0,5 - 1,5 секунды) предъявляется стимул, например, пятно света при определении абсолютной световой чувствительности в полной темноте. Как правило, испытуемому разрешается только две категории ответов (“Да”, “Нет”; “Вижу”, “Не вижу” и т.п.), форма которых точно оговаривается в инструкции испытуемому. Испытуемый отвечает, его ответ регистрируется. Предъявление стимулов осуществляется нисходящими и восходящими рядами. В первом случае степень выраженности определенного параметра стимула, чувствительность к которому измеряется, постепенно уменьшается от максимума до минимума, во втором — наоборот. Обычно измерение абсолютного порога начинается с нисходящего ряда стимулов, т.е. с отчетливо воспринимаемого стимула, изменяемый параметр которого с каждым шагом последовательно уменьшается. За порог в этом ряду принимается значение стимула, находящегося в середине межстимульного интервала между тем стимулом, который еще воспринимается, и тем, который впервые не воспринимается, т.е. середина того интервала, в котором произошла первая смена категории ответа испытуемого. В нисходящем ряду определяется порог исчезновения ощущения — Ll,в восходящем — порог появления — Lh(L — от латинского limen — порог). Чаще всего они не совпадают вследствие существования систематической ошибки.

Систематические ошибки бывают двух типов. Это так называемая ошибка привыкания, когда испытуемый продолжает повторять тот же ответ, что и на предыдущем шаге, хотя порог уже пройден и стимул в нисходящем ряду уже не вызывает ощущения, и ошибка ожидания или предвосхищения — ошибка противоположного толка. Для того, чтобы сбалансировать любую из этих ошибок, если они появляются, применяется: 1) уравновешивание числа тех и других рядов путем их чередования — нисходящие и восходящие ряды предъявляются парами, 2) требование от испытуемого ответа на каждый шаг изменения стимула в ряду. Для контроля за тщательностью работы испытуемого используется еще один экспериментальный прием — изменение длины стимульных рядов от пары к паре за счет смещения в случайном порядке начального и конечного значения стимулов в ряду. Эта предосторожность служит для предупреждения возможности повторения испытуемым своих ответных реакций на основе простого отсчета от начала и конца ряда определенного количества шагов изменения стимула1.

При выборе величины шага изменения стимула надо учитывать следующие моменты. При уменьшении величины шага падает дисперсия ответов (Геррак, 1970), а, следовательно, и порогов в восходящих и нисходящих рядах, что позволяет сократить число пар рядов, не изменяя заданной точности измерения порога. Однако, уменьшение величины шага приводит к увеличению количества шагов в каждом отдельном ряду, т.е. к удлинению ряда и, следовательно, опыта в целом. Оптимальный размер шага является результатом компромисса между стремлением к большой точности в оценке порога и нежеланием делать опыт очень длинным и утомительным.

Необходимое число измерений (пар рядов) определяется требуемой точностью измерения и степенью разброса получаемых в эксперименте данных. Его можно вычислить по формуле:

(1)

где n — число измерений; Up— квантиль нормального распределения, соответствующий заданной доверительной вероятности в определении порога; s — дисперсия пороговых значений; d — требуемая точность в определении порога.

 

Поскольку до начала опытов дисперсия пороговых значений неизвестна, для определения требуемого числа измерений необходимо провести предварительные пробные измерения, чтобы “прикинуть” величину дисперсии.

Обработка результатов. За абсолютный порог принимается среднее арифметическое всех найденных в течении опыта порогов появления и исчезновения и рассчитывается как :

 

(2)

 

где RL — средний абсолютный порог (обозначение RL — аббревиатура от немецкого “Reiz Limen”); Li— значение единичного порога в каждом стимульном ряду, как в восходящем, так и в нисходящем; N — общее число рядов.

 

Вариативность работы испытуемого оценивается средним квадратическим (стандартным) отклонением sL:

(3)

Статистическая ошибка, которая допускается, при вычислении в опыте абсолютного порога, оценивается стандартной ошибкой среднего значения:

(4)

2. Измерение дифференциального порога (DL) методом минимальных изменений.

Процедура. В этом случае все особенности метода и процедура остаются почти теми же, что и при определении абсолютного порога. Единственное изменение процедуры состоит в том, что одновременно с переменным стимулом испытуемому предъявляется эталон или стандартный стимул — Sst, который задает тот уровень исходного раздражителя, относительно которого выясняется величина разностного порога. В силу того, что ощущения различия стимулов у испытуемого могут быть различны, естественно разрешить испытуемому давать три категории ответов, а именно “больше”, “меньше”, “равно”. Ответ “не знаю”, “сомневаюсь” обычно отождествляется с ответом “равно”. За порог принимается значение стимула, соответствующее середине межстимульного интервала, где впервые произошла смена категории ответа: от “больше” к “равно” и от “равно” к “меньше” в нисходящем ряду, а в восходящем ряду от ответа “меньше” к ответу “равно” и от ответа “равно” к ответу “больше”. Таким образом, при измерении разностного порога определяются четыре значения порога (по два в каждом ряду). Это верхний порог — Lhв восходящем и нисходящем рядах ( Lh­и LhЇ) и нижний порог — Llв восходящем и нисходящем рядах (Ll­и LlЇ). Таким образом, в каждом ряду мы находим две пороговые точки: верхний и нижний разностные пороги. На рис.1 они помечены точками в каждом ряду. Этот рисунок иллюстрирует правило установления пороговой точки в нисходящих и восходящих рядах ответов испытуемого.

Рис.1. Фрагмент протокола опыта по измерению дифференциального порога:

<+>, <=> и <-> — ответы испытуемого. Точками отмечены пороги в восходящих (­) и нисходящих (Ї) рядах

Обработка данных. Сначала находим значения верхнего разностного порога путем усреднения всех верхних порогов, в каком бы ряду они не стояли:

(5)

 

где Lh­и LhЇ — значения верхних порогов в восходящем и нисходящем рядах, а n — число пар рядов.

Аналогичным образом вычисляем нижний разностный порог:

(6)

 

Верхний и нижний пороги ограничивают интервал неопределенности — IU (от английского “Interval of Uncertainty”), т.е. ту зону стимульного ряда, где преобладают ответы равенства. Иначе говоря, интервал неопределенности — это та зона стимулов, которая сверху ограничена стимулом, в среднем едва заметно отличающимся от эталонного, как больший, а снизу — стимулом, в среднем едва заметно отличающимся от эталонного, как меньший. Понятно поэтому, что IU содержит две различительные ступени или два едва заметных различия, т.е. равен двум дифференциальным порогам DL (от немецкого “Differenz Limen”):