Раздел 4. Непрерывные случайные величины и их числовые характеристики.
Тест по курсу теории вероятностей и математической статистики.
Раздел 1. Основные понятия теории вероятностей.
Задание: выберите правильный ответ и отметьте в таблице соответствующую букву.
Вариант демо
1. 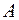 и
и 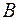 - независимые события. Тогда справедливо следующее утверждение: а) они являются взаимоисключающими событиями
- независимые события. Тогда справедливо следующее утверждение: а) они являются взаимоисключающими событиями
б) 
в) 
г) 
д) 
| а | б | в | г | д |
2.  ,
,  ,
,  - вероятности событий
- вероятности событий 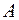 ,
, 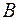 ,
,  соответственно – приведены в таблице. Отметьте в первом столбце знаками плюс и минус те ситуации, которые могут иметь место, и те, которые не могут произойти, соответственно.
соответственно – приведены в таблице. Отметьте в первом столбце знаками плюс и минус те ситуации, которые могут иметь место, и те, которые не могут произойти, соответственно.

| 
| 
| |
| а | 0.1 | 0.3 | 0.2 |
| б | 0.5 | 0.5 | 0.5 |
| в | 0.8 | 0.9 | 0.5 |
| г | 0.5 | 0.6 | 0.6 |
| д | 0.9 | 0.8 | 0.8 |
3.Вероятности событий 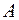 и
и 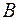 равны
равны  ,
,  . Тогда наименьшая возможная вероятность события
. Тогда наименьшая возможная вероятность события  есть:
есть:
а) 1,25 б)0,3886 в)0,25 г)0,8614
д) нет правильного ответа
| а | б | в | г | д |
4. Докажите равенство  с помощью таблиц истинности или покажите, что оно неверно.
с помощью таблиц истинности или покажите, что оно неверно.
Тест по курсу теории вероятностей и математической статистики.
Раздел 2. Вероятности объединения и пересечения событий, условная вероятность, формулы полной вероятности и Байеса.
Задание: выберите правильный ответ и отметьте в таблице соответствующую букву.
Вариант демо
1.Бросаем одновременно две игральные кости. Какова вероятность, что сумма выпавших очков не больше 6?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) нет правильного ответа
| а | б | в | г | д |
2.Каждая буква слова «РЕМЕСЛО» написана на отдельной карточке, затем карточки перемешаны. Вынимаем три карточки наугад. Какова вероятность получить слово «ЛЕС»?
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ;
;
д) нет правильного ответа
| а | б | в | г | д |
3. Среди студентов второго курса 50% ни разу не пропускали занятия, 40% пропускали занятия не более 5 дней за семестр и 10% пропускали занятия 6 и более дней. Среди студентов, не пропускавших занятия, 40% получили высший балл, среди тех, кто пропустил не больше 5 дней – 30% и среди оставшихся – 10% получили высший балл. Студент получил на экзамене высший балл. Найти вероятность того, что он пропускал занятия более 6 дней.
а)  ; б)
; б)  ; в)
; в)  ; г)
; г)  ; д) нет правильного ответа
; д) нет правильного ответа
| а | б | в | г | д |
Тест по курсу теории вероятностей и математической статистики.
Раздел 3. Дискретные случайные величины и их числовые характеристики.
Задание: выберите правильный ответ и отметьте в таблице соответствующую букву.
Вариант демо
1. Дискретные случайные величины X и Y заданы своими законами
распределения
| X | -1 | ||
| Р(Х) | 0.3 | 0.4 | 0.3 |
| Y | ||
| Р(Y) | 0.5 | 0.5 |
Случайная величина Z = X+Y. Найти вероятность 
а) 0.7; б) 0.84; в) 0.65; г) 0.78; д) нет правильного ответа
| а | б | в | г | д |
2.X, Y, Z – независимые дискретные случайные величины. Величина X распределена по биномиальному закону с параметрами n=20 и p=0.1. Величина Y распределена по геометрическому закону с параметром p=0.4. Величина Z распределена по закону Пуассона с параметром  =2. Найти дисперсию случайной величины U= 3X+4Y-2Z
=2. Найти дисперсию случайной величины U= 3X+4Y-2Z
а) 16.4 б) 68.2; в) 97.3; г) 84.2; д) нет правильного ответа
| а | б | в | г | д |
3. Двумерный случайный вектор (X,Y) задан законом распределения
| X=1 | X=2 | X=3 | |
| Y=1 | 0.12 | 0.23 | 0.17 |
| Y=2 | 0.15 | 0.2 | 0.13 |
Событие  , событие
, событие  . Какова вероятность события А+В?
. Какова вероятность события А+В?
а) 0.62; б) 0.44; в) 0.72; г) 0.58; д) нет правильного ответа
| а | б | в | г | д |
Тест по курсу теории вероятностей и математической статистики.
Раздел 4. Непрерывные случайные величины и их числовые характеристики.
Задание: выберите правильный ответ и отметьте в таблице соответствующую букву.
Вариант демо
1.Независимые непрерывные случайные величины X и Y равномерно распределены на отрезках: X на  Y на
Y на  .
.
Случайная величина Z = 3X +3Y +2. Найти D(Z)
а) 47.75; б) 45.75; в) 15.25; г) 17.25; д) нет правильного ответа
| а | б | в | г | д |
2. Непрерывная случайная величина X задана своей функцией распределения  Найти
Найти 
а) 0.5; б) 1; в) 0; г) 0.75; д) нет правильного ответа
| а | б | в | г | д |
3. Непрерывная случайная величина X задана своей плотностью вероятности  . Найти
. Найти  .
.
а) 0.125; б) 0.875; в)0.625; г) 0.5; д) нет правильного ответа
| а | б | в | г | д |
4.Случайная величина X распределена нормально с параметрами  8 и
8 и  3. Найти
3. Найти 
а) 0.212; б) 0.1295; в)0.3413; г) 0.625; д) нет правильного ответа
| а | б | в | г | д |