Методические указания по выполнению отдельных разделов курсовой работы
Цель и задачи выполнения курсовой работы
Курсовая работа, выполняемая студентами, является завершающим этапом изучения дисциплины " Информатика".
Курсовая работа является одной из важнейших форм учебной работы. Она имеет целью привить навыки самостоятельной работы, выявить знания студентов по данной дисциплине и умение применять эти знания в практической работе по выбранной ими специальности.
В процессе выполнения курсовой работы студент должен проявить способность к самостоятельной работе с учебной и научно-технической литературой, умение обобщать полученные знания, делать обоснованные выводы, формулировать рекомендации по выбору технических и программных средств для конкретной работы, продемонстрировать навыки владения ПК и пакетами прикладных программ (ППП).
В ходе выполнения курсовой работы должны быть изучены и проанализированы вопросы, связанные с различными аспектами использования компьютерной техники для решения инженерных задач.
Выполнение курсовой работы предусматривает следующие задачи:
1. Закрепление и самостоятельное использование на практике знаний в области программирования на алгоритмическом языке "Паскаль" в средах MS/DOS или WINDOWS и применение численных методов при решении инженерно-технических задач.
2. Умение отлаживать составленную программу, применяя функциональные возможности различных ЭВМ.
3. Приобретение студентами навыков использования материалов стандартов единой системы программной документации по разработке алгоритма и программы курсовой работы.
4. Умение работать в офисных приложениях Word, Excel, PowerPoint.
Тематика курсовой работы
Тематика курсовой работы формируется преподавателем в зависимости от уровня подготовки студентов и может включать следующие темы:
· вычисление приближенного значения определенного интеграла;
· вычисление корней нелинейных уравнений;
· решение систем линейных уравнений.
Выполненная курсовая работа должна содержать:
· блок-схему алгоритма программы (основной и подпрограмм);
· программу, выполненную по модульному принципу, которая должна включать основной модуль и следующие обязательные функции и подпрограммы:
· п/п описания вида функции;
· п/п вывода графика функции;
· п/п вычисления интеграла одним из методов прямоугольников;
· п/п вычисления интеграла методом трапеции;
· п/п вычисления интеграла методом Симпсона;
· п/п вычисления интеграла методом трех восьмых;
· п/п вычисления интеграла методом Ньютона-Котеса,
· п/п вычисления интеграла методом Чебышева.
Ввод исходных данных предусмотреть в программе с клавиатуры, а вывод результатов вычислений осуществить в дисковый файл и на экран монитора.
Исходные данные к курсовой работе
Исходные данные к курсовой работы выбираются по таблице (см. приложение) исходя из номера варианта студента
Задание на курсовую работу
Составить блок-схему алгоритма и написать программу на языке Паскаль, позволяющую вычислить значение определенного интеграла от функции f(x) на отрезке [a,b] с абсолютной погрешностью eps, используя известные численные методы - метод прямоугольников, трапеции, Симпсона (парабол), 3/8, Ньютона-Котеса, Чебышева в соответствии с индивидуальным заданием.
В работе программы предусмотреть ввод границ интервала интегрирования и значения погрешности с клавиатуры. В начале работы программы на экран дисплея должен выводиться график функции с оцифровкой осей и иллюстрацией одного из указанных методов интегрирования, например в виде, представленном на рис.1
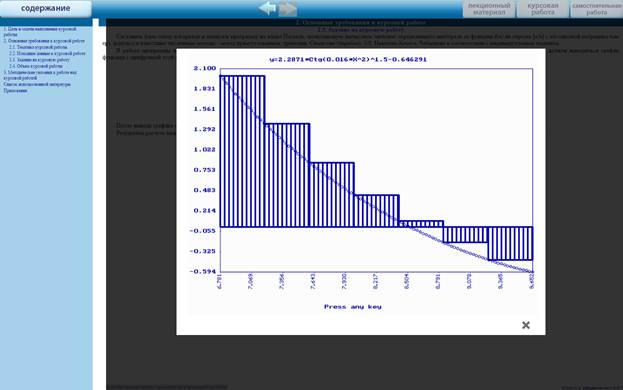
Рис. 1. График функции с иллюстрацией метода левых прямоугольников
После вывода графика функции на экран необходимо задать с клавиатуры начальное значение количества разбиений n, после чего программа должна продолжить работу.
Результаты расчета вывести на экран дисплея и в дисковый файл в виде:
КУРСОВАЯ РАБОТА
ПО КУРСУ ИНФОРМАТИКА
"ПРИБЛИЖЕННОЕ ВЫЧИСЛЕНИЕ ЗНАЧЕНИЙ ОПРЕДЕЛЕННОГО ИНТЕГРАЛА"
Выполнил: студент гр. 320771 Иванов А.Е.
Вариант 17
y = sin(x) + cos(x)
Xn=0.456 Xk=0.998 Eps=0.001
РЕЗУЛЬТАТЫ ВЫЧИСЛЕНИЙ
| Число разбиений | Метод вычисления | Точность вычисления | |||
| Левых прямоугольников | Трапеции | Симпсона | Чебышева | ||
| ... | 0.6876 0.6903 0.6922 ... 0.6924 | 0.6876 0.6903 0.6922 ... 0.6924 | 0.6922 0.6923 0.6924 ... 0.6924 | 0.6922 0.6923 0.6924 ... 0.6924 | - 0.0027 0.0019 … 0.0007... |
*** Требуемая точность достигнута при 32 разбиениях
Объем курсовой работы
Курсовая работа состоит из пояснительной записки, включающей в себя графическую и описательную части. Общий объем записки должен составлять 20-30 листов стандартного формата А4.
Графическая часть выполняется на трех-четырех листах стандартного формата А4. На листах выполняется блок-схема общего алгоритма программы согласно ГОСТ 19.701-90 "Схемы алгоритмов, программ, данных и систем".
Описательная часть пояснительной записки должна быть написана кратко, ясно и включать все необходимые описания, обоснования, рисунки и таблицы.
План построения и содержание разделов пояснительной записки к курсовой работе
Пояснительная записка включает в себя:
1. Титульный лист.
2. Индивидуальное задание на выполнение курсовой работы.
3. Оглавление.
4. Описание численных методов решения задачи (должно быть представлено подробное описание каждого из численных методов с графической иллюстрацией приближения).
5. Блок-схему алгоритма программы (приводятся блок-схемы основной программы и используемых подпрограмм).
6. Текст программы на языке Паскаль (приводится текст программы на языке программирования Паскаль).
7. Результаты работы программы, полученные в ходе выполнения программы в виде графика (возможна замена графиком функции, построенной в Excel с иллюстрацией указанного в задании метода).
8. Результаты работы программы, полученные в ходе выполнения программы в виде таблицы (приводится таблица, полученная в ходе работы программы и записанная в дисковый файл).
9. Теоретическую часть, включающую в себя (приводится краткое описание используемых в программе функций и процедур с указанием формальных и фактических аргументов).
10. Список использованных источников (приводится список источников, использованных при выполнении курсовой работы).
©2008-2016, Интернет-институт ТулГУ
Методические указания по выполнению отдельных разделов курсовой работы
При описании численных методов должно быть дано подробное описание этого метода с графической иллюстрацией
Метод прямоугольников
Сущность метода заключается в вычислении площади фигуры, ограниченной кривой подынтегральной функции, осью абсцисс и пределами интегрирования (рис.2)
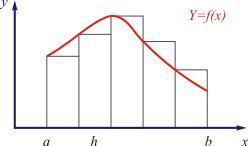
Рис.2. Иллюстрация метода левых прямоугольников
При этом интервал интегрирования [a,b] разбивается на n равных участков с шириной h, где
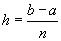 .
.
Площадь каждого отдельного участка вычисляется по формуле вычисления площади прямоугольника:
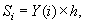
где Y(i) - значение подынтегральной функции на левой границе i-го участка.
В общем случае формула вычисления значения интеграла примет вид:
 .
.
Эта формула носит название формулы левых прямоугольников.
Блок-схема алгоритма программы для данного метода представлена на рис.3.

Рис.3. Блок-схема алгоритма метода левых прямоугольников.
Подпрограммы
При составлении программ необходимо оформлять в виде подпрограмм отдельные части программы, не зависимые друг от друга. Так как подпрограммы аналогичны программам в миниатюре, то программа в этом случае представляет собой конструкцию, состоящую из отдельных программ. Это выделение ценно по нескольким причинам: - во-первых, увеличивает наглядность и понимание программы; во-вторых является эффективным средством разработки программ, что делает процесс программирования более систематическим и регулируемым по нарастанию сложности. В языке Паскаль применяются два вида подпрограмм - функции и процедуры. Их описание должно располагаться между разделом описания переменных и разделом операторов. Структура процедур и функций аналогична структуре основной программы на ПАСКАЛЕ.
Функции
В виде функций оформляются вычисления результатом выполнения которых является одно скалярное значение, которое должно быть присвоено имени функции.
Описание функции начинается с заголовка программы и помимо раздела операторов функции, может включать следующие разделы - описание меток, констант, типов, переменных, а также локальных функций и процедур.
Общая форма записи функции:
FUNCTION <имя функции>(<список формальных параметров>):<тип>;
<разделы определений и описаний локальных параметров и подпрограмм>
begin
<операторы функции
..................
имя функции:=..........>
end;
Необходимо отметить, что тип результата задается в заголовке функции. Список формальных параметров представляет собой список переменных со своими описаниями. В функциях может быть любое фиксированное число параметров, но определять функция с переменным числом параметров нельзя. Среди входящих в функцию операторов должен присутствовать хотя бы один оператор присваивания, в левой части которого указывается имя данной функции. Этот оператор и определяет значение, вырабатываемое данной функцией. Таких операторов присваивания может быть и несколько, но при каждом конкретном обращении к функции должен выполняться только один из них.
Вызов к выполнению функции производится при каждом указании имени функции в любом выражении с последующим перечислением фактических параметров, заключенных в скобки. После выполнения функции выработанный ее результат используется в качестве значения указателя функции в том выражении, в которое входил данный указатель.
Пример.
Написать функцию, описывающую y=tan(x)+sec(x).
function y( x:real):real;
begin y:=Sin(x)/Cos(x)+1/Cos(x); end;
Процедуры
В виде процедур оформляются как вычисления, в ходе которых может быть получено несколько значений, так и вычисления когда вообще не требуется передавать результаты вызывающей программе. Описание каждой процедуры начинается с заголовка, в котором задаются имя процедуры и список формальных параметров с указанием их типов. В отличие от функции процедура может быть и без параметров, тогда в заголовке указывается только ее имя. С помощью параметров в процедуре осуществляется передача исходных данных в процедуру, а также передача результатов работы обратно в вызвавшую ее программу.
Общая форма записи процедуры:
PROCEDURE <имя> [(<список формальных параметров>)];
<разделы определений и описаний локальных параметров и подпрограмм>
begin
<................
операторы процедуры
..................
..................>
end;
Список формальных параметров у процедуры может включать в себя параметры-значения, параметры-переменные, параметры-процедуры и параметры-функции. В отличие от параметров-значений, которые представляют собой обыкновенные формальные параметры, используемые и в функциях, параметры - переменные позволяют передавать результат вычисления в вызываемую программу, без использования глобальных параметров. Описание параметра-переменной в заголовке процедуры должно начинаться со слова VAR.
procedure primer(a,b:real; var d:real; var h,m:integer)
Следует отметить, что нет никаких ограничений на порядок следования формальных параметров процедуры - порядок их следования безразличен
Вызов на выполнение процедуры осуществляется при помощи оператора процедуры:
<имя процедуры > (<список фактических параметров>);
При вызове процедуры параметры-значения передаются по значению, а параметры-переменные по ссылке. Процедуры возвращают результат в основную программу не только при помощи параметров-переменных, но и непосредственно изменяя глобальные переменные.
Между формальными и фактическими параметрами функции и процедуры должно быть полное соответствие:
· формальных и фактических параметров должно быть одинаковое количество;
· порядок следования фактических и формальных параметров должен быть один и тот же;
· тип каждого фактического параметра должен совпадать с типом соответствующего его формального параметра.
Кроме того, следует отметить, что если в качестве формального параметра используется параметр-переменная, то и фактическим параметром может быть только переменная, но не в коем случае не константа или выражение.
Для метода левых прямоугольников подпрограмма на языке паскаль может быть записана в виде:
Procedure levpr(a,b:real; n:integer; var s:real);
var i:integer;
x,h:real;
begin
s:=0;
h:=(b-a)/n;
for i:=0 to n-1 do
begin x:=a+h*i; s:=s+f(x)*h; end;
end;