Выбор банка и погашение кредита
Введение
Задача расчетного задания состоит:
· В определении с помощью финансовой функции ЧПС наиболее выгодного инвестиционного проекта и выборе с помощью финансовой функции ПЛТ банка кредитора для первоначального инвестирования выбранного проекта;
· В последующей разработке плана погашения кредита;
Анализ проектов
Финансовая функция ЧПС возвращает чистый текущий объем вклада, вычисляемый на основе ряда последовательных поступлений наличных и нормы амортизации. Чистый текущий объем вклада - сегодняшний объем будущих платежей (отрицательные значения) и поступлений (положительные значения).
Синтаксис
ЧПС (ставка; значение1; значение2;…)
ЧПС использует порядок аргументов значение1; значение2;… для определения порядка поступлений и платежей. Убедитесь в том, что Ваши платежи и поступления введены в правильном порядке.
Аргументы, которые являются числами, пустыми ячейками, логическими значениями или текстовыми представлениями чисел учитываются; аргументы, которые являются значениями ошибки или текстами, которые не могут быть преобразованы в числа, игнорируются.
Если аргумент является массивом или ссылкой, то учитываются только числа. Пустые ячейки, логические значения, тексты или значения ошибок в массиве или ссылке игнорируются.
Замечания
Считается, что инвестиция, значение которой вычисляет функция ЧПС, начинается за один период до даты денежного взноса значение1 и заканчивается с последним денежным взносом в списке. Вычисления функции ЧПС базируются на будущих денежных взносах. Если первый денежный взнос приходится на начало первого периода, то первое значение следует добавить к результату функции ЧПС, но не включать в список аргументов. Для получения более подробной информации, см. примеры ниже.
Если n - это количество денежных взносов в списке значений, то формула для функции ЧПС имеет вид:
ЧПС= 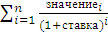 .
.
ЧПС аналогична функции ПС (текущее значение). Основное различие между функциями ПС и ЧПС заключается в том, что ПС допускает, чтобы денежные взносы происходили либо в конце, либо в начале периода. В отличие от денежных взносов переменной величины в функции ЧПС, денежные взносы в функции ПС должны быть постоянны на весь период инвестиции.
ЧПС также связана с функцией ВСД (внутренняя скорость оборота). ВСД - это скорость оборота, для которой ЧПС равняется нулю.
Примеры
Рассмотрим инвестицию, при которой Вы выплачиваете 10000 рублей через год после сегодняшнего дня и получаете годовые доходы 3000 руб., 4200 руб. и 6800 руб. в последующие три года. Предположим, что учетная ставка составляет 10%, в таком случае чистый текущий объем инвестиции составит:
ЧПС(10%; -10000; 3000; 4200; 6800) равняется 1188,44 руб.
В предыдущем примере начальный платеж 10000 руб. был включен как одно из значений, поскольку выплата производилась в конце первого периода.
Рассмотрим инвестиции, которые начинаются в начале первого периода. Допустим, Вы интересуетесь покупкой обувного магазина. Стоимость предприятия -40000 руб. и Вы ожидаете получить следующие доходы за первые пять лет: 8000 руб., 9200 руб., 10000 руб., 12000 руб. и 14500 руб. Годовая учетная ставка равна 8%. Она может представлять степень инфляции или учетную ставку конкурирующих инвестиций.
Если стоимость и доходы от обувного магазина введены в ячейки от В1 до В6 соответственно, то чистый текущий объем инвестиции в обувной магазин составит:
ЧПС(8%; В2:В6)+В1, что равняется 1922,06.
В предыдущем примере начальная цена 40000 руб. не включалась в список значений, поскольку выплата пришлась на начало периода. Предположим, что на шестой год Ваш магазин потерпел крах, и Вы предполагаете убыток в 9000 руб. для шестого года. Чистый текущий объем инвестиции в обувной магазин после шести лет составит:
ЧПС(8%; В2:В6;-9000)+В1,что равняется -3749,47.
Рассмотрим пример использования функции ЧПС.
Предположим, что стоит задача наладить производство товаров, на которые имеется спрос. При этом предстоит выбрать один из трех альтернативных проектов. Первоначальные инвестиции при реализации первого проекта составляют 508000 руб., второго – 408000 руб. и третьего - 708000.; при этом сроки службы оборудования (период инвестиции) также различаются. Все эти значения будут введены в таблицу с исходными данными. Задача заключается в определении наиболее выгодного инвестиционного проекта.
Решим эту задачу с помощью метода чистой текущей стоимости, который является одним из методов так называемого динамического расчета рентабельности инвестиции. Сущность метода заключается в том, что все будущие поступления и выплаты, происходящие в течение периода инвестиций, дисконтируются (сводятся к настоящему значению). При этом предполагается, что денежные потоки имеют место в конце каждого периода (то есть фактически учитывается сальдо денёжных потоков за период). В качестве процентной ставки используется ставка финансирования (если для финансирования проекта используются заемные средства) или ставка альтернативной возможности вложения капитала (при использовании для финансирования проекта собственных средств). Если чистая текущая стоимость инвестиции больше нуля, то инвестиция рентабельна. В этом случае нас интересует только абсолютная величина чистой текущей стоимости инвестиции (поскольку будущие платежи дисконтированы и предполагается, что возможности финансирования при данной процентной ставке не ограничены, относительная рентабельность инвестиции не имеет значения). То есть, чем больше значении чистой стоимости инвестиции, тем лучше.
Начнем рассмотрение примера с создания таблицы исходных данных. Откроем новую рабочую книгу и введем в первом рабочем листе в ячейке А1 название таблицы — Выбор проекта. В ней будут представлены не только исходные данные, но и результаты расчетов, на основании которых будет возможно принять решение о выгодности того или иного проекта.
По строкам представим исходные данные и итоги для отдельных проектов: в ячейках В5, В7 и В9следует указать текстовые метки строк Проект 1, Проект 2 и Проект 3. В строке 3 будут отображены метки столбцов, поэтому введем в ячейки D3, Е3, F3, Н3 и I3 соответственно:
Инвестиция
Срок (лет)
Ставка (%)
Текущая стоимость
Чистая стоимость
В столбце D укажите размер первоначальной инвестиции. Введете значения 508000, 408000 и 708000 для трех проектов и отформатируйте ячейки денежным стилем. Дополнительные инвестиции будут учитываться в балансе денежных потоков. Столбец Срок (лет) должен содержать данные о периоде инвестиции - 5, 5 и 8 лет соответственно. Зададим в столбце Ставка (%) для первых двух проектов процентную ставку 13,08%, а для третьего -11,08%. Отформатируйте ячейки процентным стилем. Основные исходные данные введены, присвоим первому рабочему листу имя Выбор проекта. В результате получаем таблицу, приведенную на рис. 1.
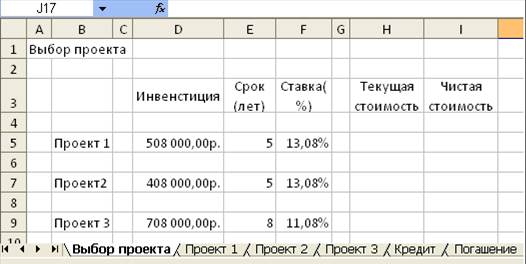
Рис. 1
Присвоим второму рабочему листу имя Проект 1. Одноименный заголовок таблицы введите и в ячейку А1. В строке 3 укажите в ячейках В3, D3, F3 и Е3 текстовые метки столбцов:
Год
Баланс денежных потоков
Текущая стоимость
Текущая стоимость (Итог).
Текущую стоимость инвестиции в первом и последующих рабочих листах будем определять отдельно. Если в первом рабочем листе для расчета текущей стоимости будем использовать функцию ЧПС, то в других листах текущую стоимость денежных потоков для каждого года рассчитаем с помощью формулы
Текущая стоимость = Денежн. поток*(1 + ставка)^(-год), а затем сложим полученные значения.
В ячейках В4 - В8 укажите значения от 1 до 5. Далее введите предполагаемые значения для денежных потоков в ячейки D4 - D8. Следует помнить, что отрицательное сальдо денежных потоков (выплаты в течение периода превышают поступления) следует указывать со знаком минус.
Теперь определим текущую стоимость денежных потоков для каждого года. Для этого в ячейку Е4 введите формулу:
=D4*(1 + Выбор проекта!$F$5)^(-B4)
и скопируйте ее в ячейки Е5 - Е8. В столбце F значение текущей стоимости инвестиции будет представлено нарастающим итогом. В ячейке F4 с помощью формулы
= Е4
задайте представление значения текущей стоимости сальдо денежных потоков для первого года. В ячейке F5 укажите формулу
= F4 + Е5
и скопируйте ее в ячейки F6 - F8. В ячейке F8 представлено значение текущей стоимости инвестиций, которое должно совпасть со значением в ячейке Н5 в рабочем листе Выбор проекта, рассчитанном с помощью функции ЧПС. В результате все этих действий получаем таблицу, представленную на рис. 2.

Рис. 2
Перейдем в третий рабочий лист и назовем его Проект 2. Чтобы не повторять всех аналогичных действий, скопируем содержимое рабочего листа Проект 1 и выполним необходимую редакцию содержимого. Отредактируем название таблицы (ячейка А1) и формулу в ячейке Е4 (ту ее часть, которая касается процентной ставки (Выбор проекта!$F$7)). В результате получаем таблицу, представленную на рис. 3.
Те же самые операции следует выполнить для четвертого рабочего листа, который называется Проект 3. Здесь только необходимо добавить данные для трех дополнительных лет (см. рис. 4). Следует не забыть указать правильный адрес ячейки для значения процентной ставки (Выбор проекта!$F$9).

Рис. 3

Рис. 4
Перейдем к рабочему листу Выбор проекта для завершения расчетов и определения наиболее выгодного проекта. В этом рабочем листе текущее значение инвестиции будем определять с помощью функции ЧПС. Поместим указатель ячейки на ячейку Н5 и активизируем Мастер функций, выберем функцию ЧПС и зададим ее аргументы следующим образом:
= ЧПС(F5;проект1!D4:D8).
В ячейках Н7 и Н9 укажите формулы:
= ЧПС(F7;проект2!D4:D8)
и
= ЧПС(F9;проект3!D4:D11).
Полученные данные должны совпасть со значениями, рассчитанными с столбцах Текущая стоимость (Итог) в рабочих листах, относящихся к соответствующим проектам. Теперь для определения чистой стоимости инвестиции следует вычесть из текущей стоимости размер первоначально осуществленных затрат. Поэтому укажем в ячейке I5 формулу:
H5-D5
и скопируем ее в ячейки I7 и I9. Результаты вычислений приведены в таблице на рис. 5.

Рис. 5
Анализ столбца Чистая стоимость показывает перспективность использования третьего проекта. Для признания проекта эффективным, как правило, необходимо, чтобы его чистая стоимость была положительной, а при сравнении альтернативных проектов предпочтение должно отдаваться проекту с более высоким значением. Из трех данных проектов наиболее выгоден последний (наибольшая чистая стоимость), т. к. здесь заложен дешевый ресурс, затраты вложены в экономном режиме. Таким образом, самым эффективным следует считать инвестицию 3-го проекта.
Выбор банка и погашение кредита
Для выбора банка кредитора используем финансовую функцию ПЛТ.
Эта функция возвращает величину выплаты за один период годовой ренты на основе постоянных выплат и постоянной процентной ставки.
Синтаксис
ПЛТ(ставка; кпер; нз; бз; тип)
здесь ставка - процентная ставка за период, кпер - общее число периодов выплат годовой ренты, нз - текущее значение - общая сумма, которую составят будущие платежи, бз - будущая стоимость или баланс наличности, который нужно достичь после последней выплаты. Если бз опущено, оно полагается равным 0 (будущая стоимость займа, например, равна 0), тип - число 0 или 1, обозначающее, когда должна производиться выплата. Если аргумент тип опущен, то он полагается равным 0.
Тип Когда нужно платить
0 В конце периода
1 В начале периода
Замечания
Выплаты, возвращаемые функцией ПЛТ, включают основные платежи и платежи по процентам, но не включают налогов, резервных платежей или гонораров, иногда связываемых с рентой.
Для нахождения общей суммы, выплачиваемой на протяжении интервала выплат, умножьте возвращаемое функцией ПЛТ значение на кпер.
Примеры
Следующая макроформула возвращает ежемесячные выплаты по займу в 10000 руб. и годовой процентной ставке 8%, которые можно выплачивать в течение 10 месяцев:
ПЛТ(8%/12; 10; 10000) равняется - 1037,03 руб.
Для того же займа, если выплаты должны делаться в начале периода, то выплата составит:
ПЛТ(8%/12; 10; 10000; 0; 1) равняется - 1030,16 руб.
Следующая макроформула возвращает сумму, которую необходимо выплачивать Вам каждый месяц, если Вы дали взаймы 5000 руб. под 12% годовых и хотите получить назад деньги за пять месяцев:
ПЛТ(12%/12; 5; -5000) равняется 1030,20 руб.
Предположим, что Вы хотите накопить 50000 руб. за 18 лет, накапливая постоянную сумму каждый месяц. Если предположить, что Вы сможете обеспечить 6% годовых на Ваши накопления, то можно использовать функцию ПЛТ, чтобы определить, сколько нужно откладывать каждый месяц:
ПЛТ(6%/12; 18*12; 0; 50000) равняется -129,08 руб. Если Вы платите 129,08 руб. с 6% накоплением в течение 18 лет, Вы получите 50000 руб.
Так как, был выбран третий проект, то следует взять кредит размером в 708000 р. сроком на восемь лет, погашать который (основной долг и проценты) предполагается равномерными платежами в конце каждого года. Запросы на финансирование были направлены в три банка, из которых пришли ответы с соответствующими условиями. Необходимо сравнить условия, определив эффективную процентную ставку, а также составить план погашения кредитов по годам.
Откроем новый рабочий лист и присвоим ему имя «Кредит».
В ячейках В7, В9, В11 рабочего листа «Кредит» вводится соответственно Банк 1, Банк 2 и Банк 3. В строке 5 будут представлены текстовые метки столбцов. Введите в ячейки С5, D5, Е5, F5, G5, I5, J5, К5, L5 следующие текстовые метки столбцов: Объем кредита, Выдача (%), Плата за оформление, Ставка (%), Срок (лет), Получено, Дизажио, Выплата (год), Выплата/Получено.
В первом столбце будет представлен объем кредита. Укажем во всех трех случаях объем кредита в 708000 р. Однако представление кредита еще не означает, что будет получена вся сумма. Кое-что (дизажио) необходимо оставить в банке, как плату за обработку и за повышенный риск, на который идет банк. Указам в ячейках D7, D9 и D11 значения 0,9508, 0,9558 и 0,9608 и сформатируем ячейки процентным стилем. Кроме того, следует оплатить издержки, возникающие при оформлении кредита, которые в нашем примере составляют 280, 330 и 380 р. В столбце Ставка следует ввести значения процентных ставок, по которым банки готовы предоставить кредит: 0,1208, 0,1358 и 0,1428 - а затем сформатировать ячейки столбца процентным стилем. Столбец Срок должен содержать значения количества лет, на которые предоставлен кредит - 8 лет. Этим завершается ввод исходных данных в таблицу. В результате получаем таблицу, приведенную на рис. 6.

Рис. 6
Теперь необходимо произвести расчеты.
Сначала определим в столбце J7 размер дизажио для первого варианта с помощью формулы:
=С7*(1 - D7).
Для определения полученной суммы следует вычесть из объема кредита дизажио и плату за оформление, поэтому в ячейке I7 следует задать формулу:
= С7-J7-E7.
Теперь можно приступить к расчету годового платежа по кредиту, который будет включать в себя как погашение основного долга, так и процентные платежи. Поместим указатель ячейки на ячейку К7 и введем функцию ПЛТ с обязательными аргументами:
=ПЛТ(F7; G7; -С7).
Остается определить в ячейке L7 (предварительно отформатированной в процентном стиле) отношение годовой выплаты к полученной сумме с помощью формулы:
= K7/I7.
Скопируем формулы изI7, J7, К7, L7 в расположенные ниже ячейки, в которых будут произведены вычисления для предложений кредита второго и третьего банков. Все результаты имеются на рис. 6.
В данном случае, можно рекомендовать к выбору первый банк с более низким годовым процентом. Кроме того, объективными критериями выбора здесь выступают размер ежегодных выплат и их отношение к полученной сумме по кредиту (наименьшие выплаты будут производиться именно в первом банке).
В новом рабочем листе рассчитаем процесс погашения взятого кредита.
Перейдем в следующий рабочий лист и присвоим ему имя Погашение. Вводите в ячейки В4,С4, D4 и Е4 следующие текстовые метки столбцов: Год, Погашение долга, Процентыи Остаток. В первом столбе в ячейках В6 - В13 будут представлены значения периодов выплаты - от 1 до 8. Ячейки С6 - С13 должны содержать суммы - части годового платежа, которые будут идти на погашение основного долга, ячейки D6 - D13 - значения выплачиваемых процентов, а ячейки Е6 - Е13 - значения остатка основного долга.
Особое внимание следует уделять последовательности ввода и копирования содержимого ячеек.
Определим размер выплачиваемых в первый год процентов. Поместите указатель ячейки на ячейку D6 и задайте в ней формулу:
=Кредит!$С$7*Кредит!$F$7.
Часть годового платежа, которая в первый год уйдет на погашение основного долга, составит (ячейка С6):
Кредит!$К$7-D6.
Остаток долга в конце первого года рассчитаем по формуле (ячейка Е6):
Кредит!$С$7-$С$6.
Выплачиваемые по долгу проценты для второго года определите в ячейке D7 с помощью формулы:
=E6*Кредит!$F$7.
Эту формулу следует скопировать в ячейки и для того, чтобы определить процентные платежи для следующих лет. Также можно скопировать формулу определения суммы погашения основного долга, заданную для первого года, в ячейки С7 - С13. В заключение в ячейке Е7следует указать формулу определенияостатка основного долга:
E6-C7
и скопировать эту формулу в ячейки Е8 - Е13. В итоге получаем таблицу, приведенную на рис. 7.

Рис.7
Список литературы
1. Андреев В.В. Табличный процессор Excel в экономических расчетах: Учеб. пос. по курсу «Технологическая обработка экономической информации». -Казань: КГЭУ, 2002. -108с.
2.Андреев В.В. Экономические расчеты в Excel: Лаб. практикум по курсам «Технологическая обработка экономической информации», «Информационные технологии в экономике», «Информационные технологии управления». -Казань: КГЭУ, 2003.
3. Андреев В.В. Информационные технологии в экономике. -Казань: КГЭУ, 2004.
4. Справочные материалы пакета Excel в Microsoft Office.
5. Андреев В.В. «Информационные технологии в экономике», «Информационные технологии управления», методические указания к расчетному заданию. –Казань: КГЭУ, 2006.