Алгоритм побудови апроксимуючої функціональної залежності.
ЗАВДАННЯ ДЛЯ ІНДІВІДУАЛЬНОЇ ДОМАШНЬОЇ РОБОТИ
Постановка задачі
Нехай у результаті досліджень одержали табличну модель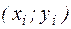 
, 
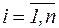, деякої функціональної залежності величини 
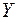від величини 
, при цьому припускається, що виміри значень 
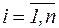, , проведені незалежно одне від одного і що похибки вимірювань підпорядковані нормальному закону розподілу випадкової величини з параметрами 
і 
, де 
, 
. Задача полягає в аналітичному представленні табличної моделі, тобто в підборі апроксимуючої функції 
, яка дає найточніше наближення до вихідних даних.
1. За допомогою метода найменших квадратів знайти параметри нелінійних залежностей визначеного типу: 
, 
, 
, 
, 
, 
.
2. За допомогою аналітичного критерію обрати вид нелінійної залежності , яка найбільш точно описує експериментальні дані 
, .
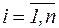3. Побудувати таблицю даних 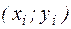, , 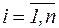і графік обраної функціональної залежності .
Варіанти до завдання
Таблиця 1.1– Варіанти до завдання
| № варіанта | і | 1 | 2 | 3 | 4 | 5 |
| 1 | 
| -6 | -4 | -1 | 0 | 1 |
|
| 0,4 | 0,2 | -1,8 | -0,7 | 0,8 | |
| 2 |
| -6 | -4 | -2 | 0 | 4 |
|
| 2,6 | 2,4 | 2,5 | 1,4 | 1,8 | |
| 3 |
| -3 | -2 | -4 | 2 | 1 |
|
| -3 | -1,3 | -0,7 | 0.3 | -0,1 | |
| Продовження Таблиці 1.1 | ||||||
| № варіанта | і | 1 | 2 | 3 | 4 | 5 |
| 4 |
| -3 | -1 | -2 | 0 | 1 |
|
| 2,3 | 2,1 | 2,2 | 1,5 | 1,4 | |
| 5 |
| -2 | -4 | 0 | 6 | 2 |
|
| -1,8 | -4,2 | -1 | -1,6 | -7,4 | |
| 6 |
| -1 | -7 | 0 | 1 | 2 |
|
| 2,9 | 3,1 | 2 | 1,9 | 3,5 | |
| 7 |
| -7 | -1 | 0 | 6 | 2 |
|
| -1,2 | -0,9 | -1 | -2,1 | -6,6 | |
| 8 |
| -1 | -7 | 0 | 1 | 2 |
|
| 2,9 | 1 | 5 | 2,3 | 3,2 | |
| 9 |
| -9 | -3 | -1 | -4 | 0 |
|
| -7,8 | 6,1 | -4,5 | -6,7 | 1,2 | |
| 10 |
| -3 | -2 | -1 | 3 | 0 |
|
| 5,6 | 5 | 2,0 | 4,3 | 1,4 | |
| 11 |
| -3 | -2 | -1 | 0 | 1 |
|
| -9,4 | -5,7 | -7,4 | -2 | -2,6 | |
| 12 |
| -5 | -2 | -1 | 0 | 1 |
|
| 4,9 | 4,3 | 4,4 | 2,3 | 2,2 | |
| 13 |
| -3 | -2 | -8 | 0 | 1 |
|
| -8,2 | -5,1 | -2,3 | 0,2 | -4,2 | |
| 14 |
| -5 | -2 | -1 | 0 | 1 |
|
| 3,5 | 4,2 | 2,8 | 1,6 | 2,7 | |
| 15 |
| -2 | -1 | 0 | 1 | 2 |
|
| -6,2 | -5,9 | -7,1 | 1,7 | -3,6 | |
| 16 |
| -2 | -1 | 0 | 1 | 2 |
|
| -2 | -4,7 | 1,5 | -4.5 | -7,1 | |
| 17 |
| -2 | -1 | 0 | 1 | 2 |
|
| -4,1 | -4 | -3,1 | -4,4 | -7,9 | |
| Продовження Таблиці 1.1 | ||||||
| № варіанта | і | 1 | 2 | 3 | 4 | 5 |
| 18 |
| -2 | -3 | -2 | -1 | 0 |
|
| -1,3 | -4,1 | -8,9 | -7,1 | -5,3 | |
| 19 |
| -3 | -2 | -1 | 0 | 1 |
|
| -5,1 | -5,5 | -3,6 | -0,3 | -2,1 | |
| 20 |
| -3 | -2 | -1 | 0 | 1 |
|
| -6,8 | -5 | -1,8 | -2 | -4,7 | |
| 21 |
| -3 | -2 | -1 | 0 | 1 |
|
| -3 | -3,8 | -2,1 | 0 | -1,7 | |
| 22 |
| -2 | -1 | 0 | 1 | 2 |
|
| -6,3 | -1,7 | 1,2 | -3,2 | -8,3 | |
| 23 |
| -4 | -3 | -2 | -1 | 0 |
|
| -4,2 | -5,2 | -5,8 | -4,4 | -3,4 | |
| 24 |
| -4 | -3 | -2 | -1 | 0 |
|
| 4,8 | 8 | 3,3 | 3,5 | 2,8 | |
| 25 |
| -2 | -7 | 0 | 1 | 2 |
|
| -2,1 | -1,6 | 0,7 | -2,5 | -5,6 | |
| 26 |
| 0 | 1 | 6 | 3 | 4 |
|
| 0,9 | 0,1 | -1,3 | 0,4 | 3,5 | |
| 27 |
| -5 | -3 | -8 | -2 | -1 |
|
| 9,5 | 5,7 | -0,2 | 0,9 | -0,8 | |
| 28 |
| 0 | 1 | 2 | 3 | 4 |
|
| 1,7 | 0,4 | -1,5 | -0,6 | 3,3 | |
| 29 |
| 0 | 1 | 8 | 3 | 4 |
|
| 0,7 | 0,1 | 0,4 | 1,5 | 4,6 | |
| 30 |
| 0 | 1 | 2 | 3 | 4 |
|
| 1,3 | 0,2 | -0,3 | 1,3 | 5,5 |
ТЕОРЕТИЧНА ЧАСТИНА
2.1 Теоретичні відомості
Необхідність встановлення форми зв’язку між ознаками виникає при проведенні теоретичних досліджень і практичних розрахунків в багатьох галузях техніки, у процесі вивчення різних питань природознавства, соціології, економіки. Вдало підібрана емпірична формула дає змогу не тільки апроксимувати сукупність експериментальних даних, “згладжуючи” значення результативної ознаки, а й екстраполювати знайдену залежність на інші проміжки значеньфакторної ознаки.
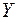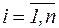Нехай у результаті досліджень одержали деяку функціональну залежність величини від величини , при цьому припускається, що виміри значень , , проведені незалежно одне від одного і що похибки вимірювань підпорядковані нормальному закону розподілу випадкової величини з параметрами і , де , .
Задача полягає в аналітичному представленні табличної моделі 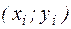, , 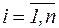тобто в підборі апроксимуючої функції , що описує результати експерименту. Функцію називають емпіричною, або рівнянням регресії y на x, параметри функції – параметрамирівняння регресії, графік функціональної залежності – лінією регресії.
Для апроксимації табличних моделей використовують метод найменших квадратів, при якому мірою наближення табличної моделі апроксимуючою функцією є сума квадратів відхилень вихідних значень і значень апроксимуючої функції 
, тобто:
.
Апроксимуючу функцію обирають так, щоб сума 
була мінімальною, що відповідає найбільш ймовірним значенням апроксимуючої функціональної залежності.
Алгоритм побудови апроксимуючої функціональної залежності.
1. Від нелінійної залежності перейти до лінійної моделі 
, використавши відповідні формули переходу до нових координат.
2. За вихідною табличною моделлю 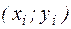, , 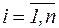побудувати нову таблицю даних 
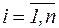, , де 
, 
.
3. Знайти параметри 
і 
лінійної моделі за формулами:
,
.
4. За відповідними формулами переходу обчислити параметри 
і 
нелінійної функціональної залежності .
5. Обрати апроксимуючу функцію за правилом: сума квадратів відхилень вихідних значень і значень апроксимуючої функції мінімальна.