Нахождение уравнений регрессии для других элементарных функций
МАТЕМАТИЧЕСКИЕ МЕТОДЫ ОБРАБОТКИ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТОВ
1. МЕТОД НАИМЕНЬШИХ КВАДРАТОВ
Пусть в результате экспериментов (например, измерений) найдены 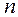 значений аргумента
значений аргумента 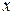 и
и 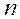 соответствующих им значений функции
соответствующих им значений функции  :
:
Таблица 1

| 
| 
| ... | 
|

| 
| 
| ... | 
|
Найти формулу, выражающую эту зависимость аналитически и принимающую значения, близкие к табличным.
Одним из распространенных методов нахождения приближающей аналитической функции является метод наименьших квадратов, который формулируется следующим образом: для функции  , заданной таблицей, найти функцию
, заданной таблицей, найти функцию  определенного вида, такую, чтобы сумма квадратов расстояний между точками
определенного вида, такую, чтобы сумма квадратов расстояний между точками  и
и 
 была наименьшей:
была наименьшей:
 (1.1)
(1.1)
Уравнение  называется уравнением регрессии
называется уравнением регрессии  на
на  .
.
На рис. 1 показана приближающая функция для заданных табличных значений (они изображены точками). Из рисунка видно, что приближающая функция представляет гладкую кривую

Рассмотрим метод нахождения приближающей функции на примере приближающей функции с  параметрами:
параметрами:

 (1.2)
(1.2)
Пусть  ,
,  . Сумма квадратов разностей соответствующих значений функций
. Сумма квадратов разностей соответствующих значений функций  и
и  имеет вид
имеет вид
 (1.3)
(1.3)
Эта сумма является функцией от параметров  Задача сводится к отысканию минимума функции
Задача сводится к отысканию минимума функции  . Используем условие экстремума:
. Используем условие экстремума:
 ,
,  , …,
, …,  ,
,
или

 (1.4)
(1.4)
………………………………………………………

Решив эту систему уравнений относительно  неизвестных
неизвестных  , найдем функцию
, найдем функцию  .
.
Значения разностей
 (1.5)
(1.5)
называются отклонениями экспериментальных значений от вычисленных по формуле (1.2). Для найденной приближающей функции сумма квадратов отклонений
 (1.6)
(1.6)
в соответствии с принципом наименьших квадратов должна быть наименьшей.
Формулы для функции с  параметрами будем использовать для приближающих функций, содержащих два и три параметра.
параметрами будем использовать для приближающих функций, содержащих два и три параметра.
Приближающие функции с двумя параметрами
В качестве приближающих функций в зависимости от характера экспериментальных данных часто используют следующие функции:
1)  5)
5) 
2)  6)
6) 
3)  7)
7) 
4)  8)
8) 
Линейная и квадратичная регрессия
Рассмотрим линейную регрессию
 (2.1)
(2.1)
Найдем частные производные по параметрам
 ,
, 
Составим систему уравнений вида (1.4)
 ,
, 
После алгебраических преобразований перепишем систему в виде


Введем обозначения
 ,
,  ,
,  (2.2)
(2.2)
 ,
, 
Тогда последняя система примет вид

 (2.3)
(2.3)
Найдем параметры  и
и  , решив систему уравнений (2.3)
, решив систему уравнений (2.3)

 (2.4)
(2.4)
Нахождение уравнений регрессии для других элементарных функций
Степенная функция (геометрическая регрессия)
 (2.5)
(2.5)
Полагая, что  и
и  , прологарифмируем формулу (2.5)
, прологарифмируем формулу (2.5)
 (2.6)
(2.6)
Введем новую функцию  , новую переменную
, новую переменную  и новые постоянные
и новые постоянные  и
и 

 ,
,  (2.7)
(2.7)
 ,
,  (2.8)
(2.8)
Введенная функцию  запишется в виде:
запишется в виде:
 (2.9)
(2.9)
т.е. задача свелась к отысканию приближающей функции в виде линейной.
Для нахождения степенной приближающей функции следует
1) пересчитать исходную таблицу  и
и  в новую таблицу значений
в новую таблицу значений  и
и  по формулам,
по формулам, 
2) для новой таблицы значений  и
и  найти постоянные
найти постоянные  и
и  ,
,
3) после определения постоянных  и
и  (см. п.1.1) , найдем постоянные
(см. п.1.1) , найдем постоянные  и
и  по формулам
по формулам
 ,
,  (2.10)
(2.10)
Показательная функция
 (2.11)
(2.11)
Логарифмируя показательную функцию (2.11), получим
 (2.12)
(2.12)
Приняв обозначения  ,
,  , перепишем (2.12) в виде
, перепишем (2.12) в виде
 (2. 13)
(2. 13)
где  , а
, а  и
и  определяются по формулам
определяются по формулам  ,
,  .
.
Для нахождения показательной приближающей функции следует
1) заменить в исходной таблице  ,
,  значения
значения  на
на  ,
, 
2) для новой таблицы значений  и
и  найти постоянные
найти постоянные  и
и  ,
,
3) после определения постоянных  и
и  (см. п.1.1) , найдем постоянные
(см. п.1.1) , найдем постоянные  и
и  по формулам
по формулам  ,
,  .
.
Дробно-линейная функция
 (2.14)
(2.14)
Введем новую приближающую функцию по формуле 
 ,
,  (2.15)
(2.15)
Из последнего равенства видно, что для нахождения параметров  и
и  по заданной таблице 1 следует составить новую таблицу, у которой значения аргумента оставить прежними, а значения функции заменить обратными числами, после чего для полученной таблицы найти приближенную функцию
по заданной таблице 1 следует составить новую таблицу, у которой значения аргумента оставить прежними, а значения функции заменить обратными числами, после чего для полученной таблицы найти приближенную функцию  . Найденные значения параметров
. Найденные значения параметров  и
и  подставить в формулу функции (2.14).
подставить в формулу функции (2.14).
Логарифмическая функция
 (2.16)
(2.16)
Очевидно, что для перехода к линейной функции следует сделать замену аргумента  по формуле
по формуле
 (2.17)
(2.17)
Новая приближающая функция примет вид
 (2.18)
(2.18)
Из формул (2.16), (2.17) видно, что для нахождения значений  и
и  нужно составить новую таблицу, в которой значения аргумента определяются по формулам (2.17) путем логарифмирования заданных
нужно составить новую таблицу, в которой значения аргумента определяются по формулам (2.17) путем логарифмирования заданных  , а значения функции те же, что в исходной таблице. Для линейной функции (2.18) описанным ранее способом найдем коэффициенты
, а значения функции те же, что в исходной таблице. Для линейной функции (2.18) описанным ранее способом найдем коэффициенты  и
и  , затем подставим их в искомую формулу (2.16).
, затем подставим их в искомую формулу (2.16).
Гипербола
 (2.19)
(2.19)
Для перехода к линейной функции сделаем замену переменной
 (2.20)
(2.20)
Новая приближающая функция запишется в виде

Для нахождения функции (2.19) следует вычислить значения нового аргумента  по формулам (2.20) и найти для новой таблицы линейную приближающую функцию. Полученные значения
по формулам (2.20) и найти для новой таблицы линейную приближающую функцию. Полученные значения  и
и  подставим в искомую формулу (2.19).
подставим в искомую формулу (2.19).