Понятие и виды случайных событий
Глава 2.
Понятие случайного события и его
Вероятности
Понятие и виды случайных событий
Как было отмечено ранее, одним из основных понятий теории вероятностей является понятие случайного события. Случайность или случай – это повседневные понятия, с которыми связан целый ряд обычных слов: наугад, риск, шанс, неопределенность, верить, ожидать и т.д. Со случайностями мы встречаемся повсюду. Традиционное отношение к ним – отрицательное. Конечно, случай может оказаться и счастливым, например, выигрыш в Спортлото. Однако счастливые исходы происходят так редко, что рассчитывать на них не имеет смысла. В основном, считается, что случайности нам мешают, путают наши планы. Лучше от них не зависеть и стараться, по возможности, исключить из нашей практики. Однако, как правило, это сделать не удается. Более того, можно привести сколь угодно примеров, где не только нецелесообразно отбросить, исключить случайность, а наоборот, необходимо изучить ее и учесть.
Например, работа станции скорой помощи. Ясно, что нельзя заранее предвидеть, когда именно потребуется скорая помощь, куда надо будет ехать, сколько времени придется затратить на того или иного больного. А ведь от этого зависит ответ на один практический вопрос: сколько дежурных врачей надо иметь, чтобы с одной стороны им не приходилось бы долго бездействовать в ожидании вызова, а с другой – больным не приходилось бы долго ждать помощи. Исключить такую случайность невозможно, следовательно, нужно не отгораживаться от нее, а постараться учесть наилучшим образом.
Итак, поскольку случайности или случайные события врываются в нашу жизнь помимо нашего желания и постоянно окружают нас, необходимо изучить их и попытаться использовать при решении тех или иных задач.
Предположим, что при определенном комплексе условий происходит какой-либо процесс, приводящий к одному из нескольких возможных исходов. Сам этот процесс со своим комплексом условий будем называть опытомили испытанием. Исходом опыта может быть результат наблюдения или измерения. Сам процесс может происходить и без участия человека. Будем также предполагать, что имеется возможность проводить каждое такое испытание неоднократно со своим неизменным (или почти неизменным) комплексом условий.
Представим теперь, что производится некоторый опыт или некоторое испытание, результат (или исход) которого не может быть заранее предсказан. Например, при броске монеты заранее нельзя сказать, как она упадет: гербом или цифрой вверх. Невозможно абсолютно точно предсказать, каков будет курс доллара по отношению к рублю через 6 месяцев? Другой пример: мы выходим к автобусной остановке, не зная расписание движения. Сколько времени нам придется ждать нужного автобуса? Заранее число минут предсказать точно нельзя.
Все эти примеры относятся к области случайных явлений. В каждом из них исход испытания заранее точно непредсказуем. Этот исход и называется случайным событием.
Случайным событиемназывается всякий факт, который в результате испытания может произойти или не произойти.
В тех случаях, когда понятно, о чем идет речь, вместо слов «случайное событие» будем использовать одно слово «событие».
Студент покупает билет «Спортлото» и отмечает в нем 6 номеров из 49. Через некоторое время публикуется список «выигравших» номеров. В этом испытании могут произойти (или не произойти), например, следующие события:
А – угадано 3 номера;
В – угадано 4 номера;
С – не угадано ни одного номера.
Конечно, приведенными событиями не исчерпывается все возможные события данного испытания.
В рассмотренном примере были введены обозначения событий, которых, в основном, будем придерживаться и в дальнейшем. Таким образом, случайные события будем обозначать большими буквами латинского алфавита: А, В, С, … и т.д.
Случайные события бывают разных видов. Рассмотрим следующий пример.
Пример 2.1. Пусть испытание состоит в том, что производится один бросок игрального кубика. Выделим несколько событий возможных в данном испытании:
А – выпало не более шести очков;
В – выпало семь очков;
С – выпало четыре очка;
D – выпало не менее четырех очков;
Е – выпало четное число очков;
F – выпало нечетное число очков.
Очевидно, что в данном испытании (1 бросок игрального кубика) событие А всегда произойдет, а событие В, наоборот, произойти не может. Такие события для конкретного испытания не являются случайными и носят названия достоверного и невозможного.
Достовернымсобытием для данного испытания называется событие, которое в этом испытании обязательно произойдет.
Достоверные события будем обозначать буквой U. Следовательно, для рассматриваемого примера А = U.
Невозможнымсобытием для данного испытания называется событие, которое в этом испытании никогда не произойдет.
Невозможные события будем обозначать буквой . Следовательно, для рассматриваемого примера В = .
Необходимо отметить, что достоверным и невозможным события являются именно для данного испытания. Изменив условия испытания можно добиться того, что эти события превратятся в случайные. Например, если предположить, что будет два броска игрального кубика и рассматривается сумма очков, выпавших на этих кубиках, то, очевидно, что событие А не вседа будет происходить в новом испытании, т.е. не будет достоверным, а событие В может появиться в этом испытании, т.е. не является невозможным.
События, содержащие только один исход, называются элементарными(или простыми).
События, содержащие более одного исхода, называются сложными(или составными).
Будем считать, что сложное событие наступило в результате испытания, если испытание закончилось одним из исходов, входящих в это событие.
Для примера 2.1 событие С является элементарным, а событие D – сложным.
Если для испытания указаны все элементарные события, которые могут в нем произойти, то говорят о том, что задано пространство элементарных событий.
Пространством элементарных событийдля данного испытания называется совокупность всех элементарных событий, возможных в данном испытании.
Элементарные события будем обозначать буквами 1, 2, …, а пространство элементарных событий буквой .
Пространство элементарных событий для испытания в примере 2.1 может быть записано следующим образом
= {1, 2, 3, 4, 5, 6,},
где 1 – выпало одно очко;
2 – выпало два очка;
3 – выпало три очка;
4 – выпало четыре очка;
5 – выпало пять очков;
6 – выпало шесть очков.
При определении этого пространства, конечно, предполагалось, что кубик в определенном смысле является «идеальной фигурой», т.е. невозможна ситуация, при которой кубик падает на ребро или вершину.
Пространство элементарных событий можно рассматривать как одно случайное составное событие. Тогда для данного испытания оно будет являться достоверным, так как в этом испытании оно всегда будет происходить.
Вернемся к примеру 2.1 и рассмотрим две пары событий С, Е и С, F. Очевидно, что при одном броске кубика события С, Е могут произойти вместе, а события С, F произойти одновременно не могут. Рассмотренные пары образуют совместные и несовместные события.
Два события называются совместными(или совместимыми) в данном испытании, если появление одного из них не исключает появление другого в этом испытании и, несовместными(или несовместимыми)в данном испытании, если появление одного из них исключает появление другого в этом испытании.
Понятно, что события С и Е являются совместными, а события С и F несовместными при одном броске игрального кубика.
Геометрически элементарные случайные события можно изобразить точками на плоскости. Пространство элементарных событий будет соответствовать области на плоскости, состоящей из всех точек, соответствующих элементарным событиям данного испытания. Любое составное событие также можно представить в виде некоторых точек области . Тогда совместные и несовместные события допускают соответственно следующую геометрическую интерпретацию (см. рис. 2.1.-2.2):
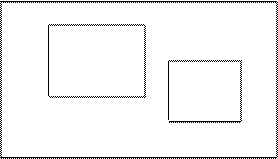
• • • • • • • • • •• • • • • • • • • •
• •А• • • • • • • • • •А• • • • • • • •
• • • • • • • • • • • • • • • • • • • •
• • • • • • • •В• • • • • • • • • •В• •
• • • • • • • • • • • • • • • • • • • •
Рис. 2.1. Рис. 2.2.
Если не фиксировать элементарные события, из которых состоят и события А и В, а рассматривать события как множества, то геометрическую интерпретацию можно упростить. Так для совместных событий рис.2.1 можно представить следующим образом:
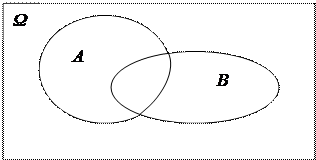 |
Рис.2.3.
Геометрическое представление на рисунке 2.3 называется диаграммой Эйлера-Венна.
Диаграммами Эйлера-Венна называются плоские фигуры, иллюстрирующие пересечение, объединение и разность конечного числа множеств.
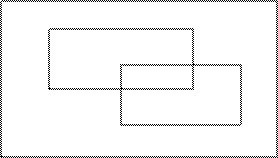
Понятие несовместности можно распространить на любое конечное число случайных событий. Для трех и более событий необходимо различать понятия попарной несовместности и несовместности в совокупности.
События А1, А2, …, Аn называются попарно несовместными, если любые два из них несовместны.
События А1, А2, …, Аn называются несовместными в совокупности, если одновременное появление всех этих событий невозможно.
Условие попарной несовместности является более сильным, чем условие несовместности в совокупности, т.е. если события попарно несовместны, то они и несовместны в совокупности. Обратное утверждение неверно. На рисунке 2.4. приведены три несовместных в совокупности события, которые не являются попарно несовместными.
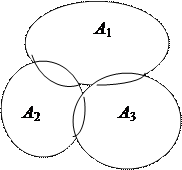
Рис. 2.4.
Нетрудно понять, что все элементарные события в одном испытании будут как несовместны в совокупности, так и попарно несовместны.
В дальнейшем, при решении задач и при выводе теорем достаточно часто будет использоваться понятие полной группы событий.
События А1, А2, …, Аn образуют полную группу событий для данного испытания, если они несовместны и в результате испытания одно из этих событий обязательно произойдет.
Геометрически это означает, что все множество, соответствующее пространству элементарных событий , события А1, А2, …, Аn делят на n частей, не имеющих между собой общих точек (см. рис. 2.5).
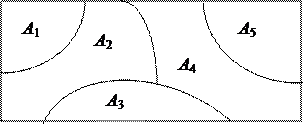 |
Рис. 2.5.
Следует отметить, что в некоторых курсах теории вероятностей в определении полной группы не входит условие несовместности событий.
Вернемся к примеру 2.1 и рассмотрим события Е – выпадение четного числа очков и F - выпадение нечетного числа очков при одном броске игрального кубика. Ясно, что, во-первых, в результате испытания одно из этих событий обязательно произойдет, во-вторых, эти события несовместны в данном испытании. Такие события называются противоположными.
Два события называются противоположнымив данном испытании, если в этом испытании они несовместны и одно из них в результате испытания обязательно произойдет.
Событие, противоположное данному событию, будем обозначать той же буквой с чертой наверху.
Очевидно, что в примере 2.1 события Е и F являются противоположными, следовательно,  или
или  .
.
Итак, в общем случае, противоположное событие дополняет событие А до полной группы или до пространства элементарных событий:
 |
Рис. 2.6.
Заметим, что достоверное и невозможное события в одном испытании являются противоположными событиями. Таким образом, если какое-то событие в данном испытании достоверно, то противоположное ему событие невозможно и наоборот.
Кроме этого, очевидно, что противоположные события А и образуют полную группу несовместных для данного испытания событий.
Полная группа несовместных событий и пространство элементарных событий для одного и того же испытания, вообще говоря, разные понятия. Если любое пространство элементарных событий можно рассматривать и как полную группу событий данного испытания, то обратное утверждение неверно. Не всякая полная группа несовместных событий будет являться пространством элементарных событий. Последнее будет выполняться только в том случае, если события, входящие в полную группу, являются элементарными. Отсюда нетрудно понять, что для каждого испытания пространство элементарных событий всегда одно, а полных групп событий (или несовместных событий) может быть несколько.
События называются равновозможными в данном испытании, если по условию испытания ни одно из них не имеет объективно большую возможность появления, чем другие.
Между случайными событиями могут существовать некоторые соотношения. Если из того, что произошло событие А следует, что произошло и событие В, то говорят, что событие А влечет за собой событие В, т.е.  . Кроме того, если одновременно
. Кроме того, если одновременно  и
и  , то события А и В являются равными, т.е.
, то события А и В являются равными, т.е.  .
.
Со случайными событиями можно проводить некоторые арифметические действия, а именно существуют понятия суммы, разности и произведения событий.