Понятия случайной величины и закона распределения вероятностей

РАЗДЕЛ II. СЛУЧАЙНЫЕ ВЕЛИЧИНЫ И ЗАКОНЫ ИХ РАСПРЕДЕЛЕНИЯ

В горячку времени стремглав!

В разгар случайностей с разбегу!

Гёте

 

Понятие случайного события и его вероятности, выработанные на уровне интуитивных представлений на протяжении XVI – XVII столетий, сразу же стали действенной силой при изучении жизненно важных процессов. С течением времени значение понятия случайного события стремительно возрастало. Одновременно выяснилось, что даже для простейших ситуаций одного этого понятия недостаточно. Действительно, в демографии, практике страхования, при рассмотрении разного рода модельных задач неизбежно встречались не только случайные события, но и некоторые величины, значения которых менялись случайным образом.

Даже в теоретических вопросах самой теории вероятностей еще на начальных стадиях ее развития появилась необходимость рассмотрения не случайных событий, а некоторых величин, значения которых появлялись с некоторыми вероятностями. Так в задачах, связанных с испытаниями Бернулли уже можно было бы рассмотреть величину, равную числу появлений конкретного события при заданном числе испытаний.

Так постепенно в науку входило новое понятие – понятие случайной величины, которое самим ходом развития знаний становилось необходимым.

Глава 5.

Случайная величина, ее виды и закон

Распределения

Понятия случайной величины и закона распределения вероятностей

В различных научных исследованиях, да и просто в жизни, часто приходится сталкиваться с величинами, которые принимают различные значения в зависимости от случайных обстоятельств. Например, количество звонков, поступивших на телефонную станцию в течение ближайшего часа, величина спроса на некий товар в течение определенного промежутка времени, число очков, выпавших при одном броске игрального кубика и т.д. При попытке хотя бы приближенно оценить значения этих величин или подобных им можно столкнуться с некоторыми, а иногда и достаточно большими трудностями. Величины, значения которых зависят от некоторых случайностей, естественно назвать случайными.

Случайной величиной называется величина, которая в результате испытания случайно принимает одно значение из множества возможных значений.

Студент идет сдавать экзамен. Оценка, которую он получит – случайная величина, множество возможных значений которой числа 2, 3, 4, 5.

Случайные величины будем обозначать большими буквами латинского алфавита: Х, У, Z и т.д., а их возможные значения соответствующими маленькими буквами с индексами. Например, для случайной величины Х ее возможные значения – х₁, х₂, … .

Рассмотрим несколько примеров.

Пример 1. Х – число очков, набранных при одном выстреле в мишень.

Пример 2. Х – число очков, выпавших при одном броске игрального кубика.

Пример 3. Х – число вызовов, поступивших от абонентов на телефонную станцию в течение определенного промежутка времени.

Пример 4. Х – время работы компьютера до первого сбоя.

Пример 5. Х – расстояние, которое пролетит снаряд при выстреле из некоторого орудия.

Пример 6. Х – вес яблока, сорванного со случайно выбранной яблони.

В первых трех примерах случайная величина Х может принимать отдельные изолированные значения, которые можно заранее перечислить. Так для случайной величины Х из примера 2 ее возможными значениями будут числа 1, 2, 3, 4, 5, 6. Для случайной величины из примера 3 возможными значениями будут числа 1, 2, 3, 4, … и т.д. Таким образом, значения этих величин можно перечислить или записать в виде некоторой последовательности чисел. Такие величины будем называть дискретными.

Дискретной случайной величиной называется случайная величина, множество возможных значений которой конечно или счетно, или иначе, представимо в виде конечной или бесконечной последовательности чисел.

Заметим, что значения дискретной случайной величины отделены друг от друга промежутками, в которых нет других возможных ее значений, поэтому дискретную случайную величину иногда называют прерывной.

В 4, 5 и 6 примерах значения случайной величины не отделены друг от друга, а заполняют некоторый интервал. Границы этого интервала могут быть приблизительно найдены из смыслового содержания величины (пример 6) или неопределены (пример 4).

Непрерывной случайной величиной называется случайная величина, множество значений которой сплошь заполняют некоторый конечный или бесконечный промежуток.

Очевидно, что для непрерывной случайной величины, в отличие от дискретной, одно значение нельзя отделить от другого некоторым промежутком.

Отметим, что данное определение непрерывной случайной величины является не совсем точным. Более строгое определение будет дано позже, после рассмотрения понятия так называемой функции распределения.

Случайная величина непосредственно связана со случайными событиями. Появление тех или иных значений случайной величины можно рассматривать как случайные события одного испытания. Предположим, что производится некоторое испытание, в результате которого может произойти случайное событие. Если пространство элементарных событий этого испытания (или полная группа событий) состоит из событий, которые имеют числовое значение, то это пространство можно рассматривать как множество значений некоторой случайной величины, связанной с данным испытанием.

Например, испытание – один бросок игрального кубика. Пространство элементарных событий состоит из шести событий, определяемых числами – один, два, три, четыре, пять и шесть очков. Тогда, очевидно, это пространство будет являться множеством значений для случайной величины Х, определяемой как число очков, выпавших при одном броске игрального кубика.

Если элементарные события не связаны с каким-либо числом, то можно искусственно дополнить эту связь. Например, испытание состоит в одном броске монеты. Пусть одна сторона монеты, к примеру, герб будет соответствовать числу ноль, а решка – числу один. Тогда пространство элементарных событий данного испытания: выпал герб, т.е. число 0 и выпала решка, т.е. число 1 будет являться множеством значений случайной величины Х, равной числу очков, выпавших при одном броске монеты.

Так как разные значения случайной величины можно рассматривать как события, а, как известно, случайные события имеют вероятность, то и значения случайной величины имеют также свои вероятности. В этом и проявляется "случайный" характер случайной величины. Например, случайная величина Х, равная числу очков, выпавших при одном броске игрального кубика, принимает значение равное 1 (выпало одно очко) с вероятностью 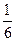, а значение равное 9 (невозможное событие) с вероятностью равной 0. Таким образом, для полного определения случайной величины необходимо указать какое-либо правило нахождения вероятностей значений этой случайной величины, т.е. задать ее закон распределения.

Законом распределения случайной величиныназывается любое правило, по которому можно находить вероятности произвольных событий, связанных со случайной величиной.

Это правило может быть задано в виде таблицы, формулы, графика, функции и т.д. Чаще всего, это бывает формула нахождения вероятности того, что случайная величина примет какое-то значение, или, что случайная величина попадет на какой-нибудь интервал.

Существуют стандартные формы задания закона распределения случайной величины, причем эти формы, кроме одной, являются различными для дискретных и непрерывных случайных величин. Наиболее простые формы закона распределения имеет дискретная случайная величина.