
Категории:
АстрономияБиология
География
Другие языки
Интернет
Информатика
История
Культура
Литература
Логика
Математика
Медицина
Механика
Охрана труда
Педагогика
Политика
Право
Психология
Религия
Риторика
Социология
Спорт
Строительство
Технология
Транспорт
Физика
Философия
Финансы
Химия
Экология
Экономика
Электроника
График функции многих переменных. Линии уровня
Функции нескольких переменных
Методические указания и контрольная работа для студентов первого курса всех специальностей
Ухта 2003
УДК 514.742.4(075)
Мотрюк Е.Н., Мужикова А.В., Зубкова С. Е. Функции нескольких переменных: Методические указания. – Ухта: УГТУ, 2003.– 42с. ил.
Методические указания предназначены для студентов первого курса всех специальностей. В методических указаниях даны основные сведения о функциях нескольких переменных и их приложениях. Приведено достаточное количество примеров с подробным описанием решения.
Содержание указаний соответствует рабочей программе.
Методические указания рассмотрены и одобрены кафедрой высшей математики УГТУ от 19.06.03 пр. №10.
Рецензент – Волкова И.И., доцент, к.т.н.
Редактор – Баскакова Ю.Л., ст. преп. каф. ВМ.
В методических указаниях учтены предложения рецензента и редактора
План 2003г., позиция 92
Подписано в печать 01.11.2001г.
Объем 16 м.п.л. тираж 25 экз. Заказ.171
2003г., Ухта, ул. Первомайская, 13.
СОДЕРЖАНИЕ
| ГЛАВА 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ | |
| § 1.1. Понятие функции многих переменных. График и линии уровня функции двух переменных. | 3-8 |
| § 1.2. Предел функции нескольких переменных в точке. Непрерывность функции в точке и на множестве. | 8-13 |
| ГЛАВА 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ | |
| § 2.1. Частные производные функции нескольких переменных. Полный дифференциал. Линеаризация функций | 13-18 |
| §2.2. Дифференцирование сложных и неявных функций. Касательная пи нормаль к поверхности. | 18-23 |
| ГЛАВА 3. ПРИМЕНЕНИЯ ЧАСТНЫХ ПРОИЗВОДНЫХ | |
| §3.1. Производная по направлению. Градиент. | 23-26 |
| §3.2 Касательная плоскость и нормаль к поверхности. | 26-27 |
| §3.3. Экстремум функции двух переменных. | 27-35 |
| КОНТРОЛЬНАЯ РАБОТА | 35-37 |
| ТИПОВОЙ РАСЧЕТ | 37-41 |
| Библиографический список |
ГЛАВА 1. ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ
§ 1.1. Понятие функции многих переменных. График и линии уровня функции двух переменных.
Определение функции многих переменных
Определение. Переменная 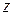 называется функцией двух переменных
называется функцией двух переменных  и
и  , если каждой паре
, если каждой паре  значений двух независимых друг от друга переменных величин
значений двух независимых друг от друга переменных величин  и
и  из некоторой области
из некоторой области  соответствует определенное значение
соответствует определенное значение  ,
,  .
.
Определение. Переменная величина  называется функцией от
называется функцией от  переменных
переменных  , если каждому набору этих независимых друг от друга переменных величин соответствует единственное значение переменной
, если каждому набору этих независимых друг от друга переменных величин соответствует единственное значение переменной  :
:  ,
,  .
.
Всякая функция нескольких переменных становится функцией меньшего числа переменных, если часть их зафиксировать. Например, функции  , где
, где  и
и  постоянные, являются функциями соответственно трех, двух и одной переменной.
постоянные, являются функциями соответственно трех, двух и одной переменной.
В дальнейшем будем рассматривать, в основном, функции двух переменных.
График функции многих переменных. Линии уровня
Определение. Множество  всех точек
всех точек  , при которых
, при которых  имеет смысл, называется областью определения, а множество значений
имеет смысл, называется областью определения, а множество значений  , принимаемых функцией
, принимаемых функцией  при
при  , называется областью изменения
, называется областью изменения  или множеством значений функции. Линия, ограничивающая область
или множеством значений функции. Линия, ограничивающая область  , называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается
, называют границей области. Точки области, не лежащие на границе, называются внутренними. Область, состоящая из одних внутренних точек, называется открытой. Область с присоединенной к ней границей называется замкнутой, обозначается  .
.
Для наглядного геометрического представления используют линии уровня для функции двух переменных и поверхностей уровня для функции трех переменных.
Определение. Множество точек пространства  с координатами
с координатами  при всех
при всех  определяет некоторую поверхность, которая называется графиком функции
определяет некоторую поверхность, которая называется графиком функции  .
.
Определение. Линией уровня функции двух переменных  называется множество всех точек плоскости
называется множество всех точек плоскости  , в которых функция
, в которых функция 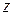 принимает постоянные значение, т.е.
принимает постоянные значение, т.е.  , где
, где  - постоянная.
- постоянная.
Определение. Поверхностью уровня функции трех переменных  называется множество всех точек плоскости
называется множество всех точек плоскости  , в которых функция
, в которых функция  принимает постоянные значение, т.е.
принимает постоянные значение, т.е.  , где
, где  - постоянная.
- постоянная.
Пример 1.1.1 Выразить объем прямоугольного параллелепипеда, вписанного в шар радиуса  как функцию двух его измерений
как функцию двух его измерений  и
и  . Найти область определения этой функции.
. Найти область определения этой функции.
Исходим из построенного чертежа (рис.1). Обозначим два измерения, скажем,  . Пусть
. Пусть  - радиус шара, тогда
- радиус шара, тогда  .
.
 Рисунок 1
Рисунок 1
| Объем параллелепипеда равен  , ,  и нам надо выразить и нам надо выразить  через через  . Из . Из  имеем имеем  , а из , а из  получаем получаем  . Значит, . Значит,  , а тогда , а тогда  - искомая функция двух переменных. - искомая функция двух переменных.
|
Ее область определения:  , т. е. круг
, т. е. круг  радиуса
радиуса  с центром в начале координат.
с центром в начале координат.
Под функцией  будем также понимать функцию точки
будем также понимать функцию точки  с координатами
с координатами  и
и  . Значением функции
. Значением функции  в точке
в точке  обозначают
обозначают  и называют частным значением функции.
и называют частным значением функции.
Пример 1.1.2. Дано:  . Найти:
. Найти:
А) 
В)  .
.
А) Чтобы найти  , надо в выражении для
, надо в выражении для  подставить
подставить  и выполнить указанные действия. Имеем
и выполнить указанные действия. Имеем  .
.
В)  .
.
Пример 1.1.3. Дано:  . Найти
. Найти  .
.
Введем обозначения

Тогда

 .
.
Из  следует, что
следует, что 
Пример 1.1.4. Найти область определения и множество значений функции  . Построить график этой функции и линии уровня
. Построить график этой функции и линии уровня  .
.
Действие извлечения корня возможно при условии  . Это неравенство определяет замкнутый круг радиуса
. Это неравенство определяет замкнутый круг радиуса  с центром в начале координат
с центром в начале координат  .
.
 Рисунок 2
Рисунок 2
| Данная функция определяется уравнением сферы  , а значит ее графиком , а значит ее графиком  является верхняя полусфера (рис.2). Линиями уровня являются окружности является верхняя полусфера (рис.2). Линиями уровня являются окружности  при условии при условии  . Отсюда, в частности, следует, что множество значений функции - отрезок . Отсюда, в частности, следует, что множество значений функции - отрезок 
|
Пример 1.1.5. Найти область определения функции 
 Рисунок 3.
Рисунок 3.
| Область определения этой функции задается неравенствами  . Первые два неравенства определяют квадрат в плоскости . Первые два неравенства определяют квадрат в плоскости  , а условие , а условие  Rозначает, что каждая прямая, проходящая через точку квадрата перпендикулярно ему, принадлежит области определения. Значит, Rозначает, что каждая прямая, проходящая через точку квадрата перпендикулярно ему, принадлежит области определения. Значит,  - бесконечный в направлении - бесконечный в направлении  параллелепипед (рис.3). параллелепипед (рис.3).
|
Пример 1.1.6. Найти линии уровня функции  .
.
Линии уровня  определяются уравнением
определяются уравнением  . Это полупарабола, расположенная в первой четверти при
. Это полупарабола, расположенная в первой четверти при  , во второй четверти плоскость
, во второй четверти плоскость  при
при  , и полуось
, и полуось  если
если 
Упражнения к §1.1.
1) Выразить площадь  равнобочной трапеции как функцию трех величин: длин оснований
равнобочной трапеции как функцию трех величин: длин оснований  и
и  и боковой стороны
и боковой стороны 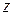 .
.
2) Выразить площадь треугольника как функцию длин двух его сторон  и
и  при условии, что известен полупериметр треугольника
при условии, что известен полупериметр треугольника 
3) Выразить объем конуса  как функцию его образующей
как функцию его образующей  и высоты
и высоты  . Указать область определения этой функции.
. Указать область определения этой функции.
4) Дана функция  Найти:
Найти:
a) 
b) 
c) 
d) 
e) 

f) 
5) Для функции  найти:
найти:
a) 
b) 
c) 
d) 
6) Найти  , если
, если 
7) Найти  , если
, если 
8) Найти и изобразить области определения следующих функций:
a) 
b) 
c) 
d) 
e) 
9) Найти линии уровня данных функций:
a) 
b) 
c) 
d) 
§ 1.2. Предел функции нескольких переменных в точке. Непрерывность функции в точке и на множестве.
Предел функции в точке
Определение. Множество всех точек  плоскости, координаты которых удовлетворяют неравенству
плоскости, координаты которых удовлетворяют неравенству  , называется
, называется  –окрестностью точки
–окрестностью точки  . Другими словами,
. Другими словами,  –окрестность точки
–окрестность точки  – это внутренние точки круга с центром
– это внутренние точки круга с центром  и радиусом
и радиусом  .
.
Определение. Пусть функция  определена в окрестности точки
определена в окрестности точки  , кроме, может быть, самой этой точки. Число
, кроме, может быть, самой этой точки. Число  называется пределом функции
называется пределом функции  при
при  , если для любого
, если для любого  существует
существует  такое, что для всех
такое, что для всех  и удовлетворяющих неравенству
и удовлетворяющих неравенству  выполняется неравенство
выполняется неравенство  . Записывают:
. Записывают:  или
или  .
.
Из определения следует, что если предел существует, то он не зависит от пути, по которому  стремится к
стремится к  .
.
Пример 1.2.1. Найти предел  .
.
Будем приближаться к  по прямой
по прямой  , где
, где  –некоторое число. Тогда
–некоторое число. Тогда  .Функция
.Функция  в точке
в точке  предела не имеет, так как при разных значениях
предела не имеет, так как при разных значениях  предел функции не одинаков.
предел функции не одинаков.
Предел функции двух переменных обладает теми же свойствами, что и предел функции одной переменной.
Пример 1.2.2. Найти предел  .
.
Исходя из того, что  при
при  , используя известную формулу
, используя известную формулу  и одно из свойств предела
и одно из свойств предела  , легко заключаем, что
, легко заключаем, что  .
.
Пример 1.2.3. Вычислить предел  .
.
Если  , то
, то  , т.е.
, т.е.  –величина бесконечно малая. Множители
–величина бесконечно малая. Множители  и
и  являются величинами ограниченными, а потому (произведение бесконечно малой на величину ограниченную есть величина бесконечно малая)
являются величинами ограниченными, а потому (произведение бесконечно малой на величину ограниченную есть величина бесконечно малая)  . Здесь считаем
. Здесь считаем  и
и  ,
,  .
.
Пример 1.2.4. Вычислить предел  .
.
Обозначим  . Тогда при
. Тогда при  имеем
имеем  . Следовательно,
. Следовательно,  .
.
Пример 1.2.5. Вычислить предел  .
.
Условие  преобразуем в условие
преобразуем в условие  при помощи подстановок
при помощи подстановок  . Получаем
. Получаем  . Из неравенства Коши имеем
. Из неравенства Коши имеем  . А тогда
. А тогда  , и поэтому
, и поэтому  . И поскольку
. И поскольку  , то заключаем, что
, то заключаем, что  .
.
Непрерывность функции в точке
Определение. Функция  называется непрерывной в точке
называется непрерывной в точке  , если она:
, если она:
a) определена в этой точке и ее окрестности,
b) имеет предел  ,
,
c) этот предел равен значению функции  в
в  , т.е.
, т.е.  или
или  .
.
Пример 1.2.6. Непрерывна ли функция  при
при  .
.
Проверяем условия непрерывности функции в  .
.
1. Функция  определена в окрестности этой точки.
определена в окрестности этой точки.
2.  , так как имеем
, так как имеем  , а
, а  ограничена.
ограничена.
3. Предел в точке равен значению функции в этой точке  .
.
Функция непрерывна в точке  . Заметим, что эта функция непрерывна в каждой точке
. Заметим, что эта функция непрерывна в каждой точке  как комбинация непрерывных элементарных функций.
как комбинация непрерывных элементарных функций.
Функции, непрерывные на множестве
Функция, непрерывная в каждой точке некоторой области, называется непрерывной в этой области. Точки, в которых нарушается условие непрерывности, называются точками разрыва этой функции. Точки разрыва  могут образовать целые линии разрыва. Так, функция
могут образовать целые линии разрыва. Так, функция  имеет линию разрыва
имеет линию разрыва  .
.
Пользуясь определением непрерывности и теоремами о пределах, можно доказать, что арифметические операции над непрерывными функциями и построение сложной функции из непрерывных функций приводит к непрерывным функциям–подобные теоремы имели место для функции одной переменной.
Определение. Областью называется множество точек плоскости, обладающих свойствами открытости и связности.
Свойство открытости: каждая точка принадлежит ей вместе с некоторой окрестностью этой точки.
Свойство связности: любые две точки области можно соединить непрерывной линией, целиком лежащей в этой области.
Определение. Точка  называется граничной точкой области
называется граничной точкой области  , если она не принадлежит
, если она не принадлежит  , но в любой окрестности ее лежат точки этой области. Совокупность граничных точек
, но в любой окрестности ее лежат точки этой области. Совокупность граничных точек  называется границей
называется границей  . Область
. Область  с присоединенной к ней границей называется замкнутой областью и обозначается
с присоединенной к ней границей называется замкнутой областью и обозначается  . Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса
. Область называется ограниченной, если все ее точки принадлежат некоторому кругу радиуса  . В противном случае область называется неограниченной.
. В противном случае область называется неограниченной.
Примером неограниченной области может служить множество точек первого координатного угла. Примером ограниченной-  -окрестность точки
-окрестность точки  .
.
Теорема 1.2.1. Если функция  непрерывна в ограниченной замкнутой области, то она в этой области:
непрерывна в ограниченной замкнутой области, то она в этой области:
a) ограничена, т.е. существует такое число  , что для всех точек
, что для всех точек  в этой области выполняется неравенство
в этой области выполняется неравенство  ;
;
b) имеет точки, в которых принимает наименьшее  и наибольшее
и наибольшее  значения;
значения;
c) принимает хотя бы в одной точке области любое численное значение, заключенное между  и
и  .
.
Упражнения к §1.2.
1) Вычислить пределы:
a) 
b) 
c) 
d) 
e) 
2) Найти пределы:
a) 
b) 
c) 
d) 
e) 
f) 
3) Исследовать на непрерывность данные функции в указанных точках:
a)  в точке
в точке 
b)  в точке
в точке 
c)  в точке
в точке 
ГЛАВА 2. ПРОИЗВОДНЫЕ И ДИФФЕРЕНЦИАЛЫ
§ 2.1. Частные производные функции нескольких переменных. Полный дифференциал. Линеаризация функций
Определение частных производных.
Рассмотрим функцию двух переменных  , определенную и непрерывную в некоторой области
, определенную и непрерывную в некоторой области  . Считаем, что точки с координатами
. Считаем, что точки с координатами  где
где  – приращения аргументов, также принадлежат области
– приращения аргументов, также принадлежат области  .
.
Определение. Частными приращениями функции  по независимым переменным
по независимым переменным  и
и  называются разности
называются разности
 , ,  . .
| (1) |
Определение. Полным приращением функции  , соответствующим приращениям аргументов
, соответствующим приращениям аргументов  и
и  , называется разность
, называется разность

| (2) |
Заметим, что в общем случае 
Пример 2.1.1. Найти частное и полное приращение функции  в точке
в точке  при приращениях аргументов
при приращениях аргументов  и
и  .
.
Принимаем  . Сначала определим
. Сначала определим  . Далее,
. Далее,
 ;
;
 ;
;
 .
.
Таким образом, используя формулы (1) и (2), получаем
 ;
;
 ;
;
 .
.
Очевидно,  .
.
Определение. Частной производной функции  по независимым переменным
по независимым переменным  и
и  называется передел отношения соответствующего частного приращения
называется передел отношения соответствующего частного приращения  и
и  к приращению данной переменной, при условии, что приращение переменной стремится к нулю:
к приращению данной переменной, при условии, что приращение переменной стремится к нулю:

| (3) |
Приняты также обозначения:  .
.
Аналогично по другой переменной.
Пример 2.1.2. Найти частные производные функции 


Геометрическая интерпретация частных производных функции двух переменных
 Рисунок 4.
Рисунок 4.
| График функции  есть некоторая поверхность. График есть некоторая поверхность. График  есть линия пересечения этой поверхности с плоскостью есть линия пересечения этой поверхности с плоскостью  . Исходя из геометрического смысла производной для функции одной переменной, заключаем, что . Исходя из геометрического смысла производной для функции одной переменной, заключаем, что  , где , где  -угол между осью -угол между осью  и касательной, проведенной к кривой и касательной, проведенной к кривой  в точке в точке  (рис. 4). (рис. 4).
|
Аналогично,  .
.
Определение. Частные производные  называются частными производными первого порядка, их можно рассматривать как функции от
называются частными производными первого порядка, их можно рассматривать как функции от  . Эти функции могут иметь производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:
. Эти функции могут иметь производные, которые называются частными производными второго порядка. Они определяются и обозначаются следующим образом:

| |

| |

| |

| (4) |
Частные производные, взятые по различным порядкам, называются смешанными.
Аналогично определяются частные производные 3-го, 4-го и т.д. порядков.
Частные производные функции двух и более переменных определяется по тем же формулам и правилам, что и функции одной переменной. Следует помнить только одно правило: если по одной переменной дифференцируем, то остальные считаем постоянными.
Пример 2.1.3. Найти частные производные второго порядка функции 
Так как  и
и  , то
, то  и
и  . Смешанные производные
. Смешанные производные  и
и 
Теорема 2.1.2 (Шварц). Если частные производные высшего порядка непрерывны, то смешанные производные одного порядка, отличающиеся лишь порядком дифференцирования, равны между собой.
В частности, для  имеем
имеем 
Дифференциал функции. Линеаризация функций
Определение. Если функция  обладает частными производными
обладает частными производными  , непрерывными в точке
, непрерывными в точке  , то по теореме Лагранжа для функций одной переменной получаем
, то по теореме Лагранжа для функций одной переменной получаем  . Это выражение представляет собой главную, линейную часть приращения функции и называется дифференциалом этой функции в данной точке.
. Это выражение представляет собой главную, линейную часть приращения функции и называется дифференциалом этой функции в данной точке.
Обозначение:  . Здесь
. Здесь  . Приняты также обозначения:
. Приняты также обозначения:  – частные дифференциалы функции
– частные дифференциалы функции 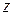 , тогда
, тогда

| (5) |
– полный дифференциал функции 
Пример 2.1.5. Найти полный дифференциал функции 
Здесь имеем место с производными сложной функции и дроби.


Ввиду симметрии выражения  относительно
относительно  и
и 
 можно писать сразу
можно писать сразу

После преобразований получаем





Определение. Если полное приращение  функции
функции  в точке
в точке  можно представить в виде
можно представить в виде  , где
, где  и
и  не зависят от
не зависят от  и
и  , а
, а  при
при  , то функция
, то функция  называется дифференцируемой в точке
называется дифференцируемой в точке  .
.
Теорема 2.1.3. Для того чтобы функция  была дифференцируема в данной точке, достаточно, чтобы она обладала частными производными, непрерывными в этой точке.
была дифференцируема в данной точке, достаточно, чтобы она обладала частными производными, непрерывными в этой точке.
Определение. Линеаризацией функции  в окрестности точки
в окрестности точки  называется приближенное равенство (тем точнее, чем меньше
называется приближенное равенство (тем точнее, чем меньше  и
и  ):
):

| (6) |
Это соотношение используется в приближенных вычислениях: дифференцируемую функцию можно заменить линейной функцией в окрестности рассматриваемой точки.
Пример 2.1.4. Вычислить приближенно 
Рассмотрим функцию  Тогда
Тогда  , где
, где  . Воспользуемся формулой (6), предварительно найдя
. Воспользуемся формулой (6), предварительно найдя  :
:  ,
,  . Следовательно,
. Следовательно,  .
.
Упражнения к §2.1.
1) Найти частное и полное приращения данной функции в данной точке и при данных приращениях аргументов:
a) 
b) 
c) 
2) Найти полные приращения данных функций в данных точках (или при переходе от точки  к
к  ):
):
a) 
b) 
c) 
3) Найти частные производные данных функций:
a) 
b) 
c) 
d) 
e) 
4) Вычислить приближенно:
a) 
b) 
c) 
d) 
e) 
f) 
§2.2. Дифференцирование сложных и неявных функций. Касательная пи нормаль к поверхности.
Случай одной независимой переменной
Предположим, что  -дифференцируемая функция двух переменных
-дифференцируемая функция двух переменных  и
и  в некоторой области
в некоторой области  , а аргументы
, а аргументы  и
и  являются дифференцируемыми функциями некоторой переменной
являются дифференцируемыми функциями некоторой переменной  , т.е.
, т.е.  . Тогда
. Тогда  -функция одной переменной.
-функция одной переменной.
Теорема 2.2.1.Имеет место равенство
 . .
| (7) |
Если  совпадает с одним из аргументов, скажем,
совпадает с одним из аргументов, скажем,  , то
, то

и  называется полной производной функции
называется полной производной функции 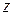 по
по  .
.
Пример 2.2.1. Найти  , если
, если  , и
, и  .
.
Непосредственная подстановка не упрощает функцию, поэтому применяем формулу (6).
 ,
,  ,
,  ,
,  .
.
В результате можно как сохранить переменные  и
и  , так и заменить их через
, так и заменить их через  (в зависимости от того, что проще). Ответ оставим в таком виде:
(в зависимости от того, что проще). Ответ оставим в таком виде:
 .
.
Случай нескольких независимых переменных
Если аргументы  и
и  функции
функции  являются функциями двух переменных, скажем,
являются функциями двух переменных, скажем,  , то
, то  также является функцией двух переменных
также является функцией двух переменных  и
и  .
.
Теорема 2.2.2 Имеют место формулы
 и и 
| (8) |
Структура этих формул сохраняется и при более большем числе переменных.
Пример 2.2.2. Найти  и
и  , если
, если 
Применим формулы (8):


Составляя суммы соответствующих произведений:


Ответ можно оставить в такой форме, или выразить через  и
и  (т.е. основные переменные):
(т.е. основные переменные):


Дифференциал сложной функции
Дифференциал сложной функции  , где
, где  , можно получить, если по формуле дифференциала
, можно получить, если по формуле дифференциала

заменить
 , ,  . .
| (9) |
В результате подстановки и перегруппировки членов при  приходим к формуле
приходим к формуле
 , ,
| (10) |
Показывающий, что форма дифференциала не зависит от того, являются ли  и
и  независимыми переменными или функциями других переменных. Это свойство называется инвариантностью формы первого дифференциала.
независимыми переменными или функциями других переменных. Это свойство называется инвариантностью формы первого дифференциала.
Пример 2.2.3. Найти дифференциал функции  , если
, если 
 .
.
Поскольку  ,то найдем все эти величины.
,то найдем все эти величины.
 по (8)
по (8)
 .
.
Подставив в  :
:
 .
.
Подставим выражения для  и
и  и перегруппируем члены, выделяя множители при
и перегруппируем члены, выделяя множители при  и
и  :
:



