Неявная функция одной переменной

Функция называется неявной, если она определена уравнением , неразрешенным относительно .

Это значит, что при каждом значении , при котором неявная функция определена, она принимает единственное значение так, что .

Теорема 2.2.3. Если –дифференцируемая функция переменных и в некоторой области и , то уравнение определяет однозначно неявную функцию , также дифференцируемую, и ее производная находится по формуле

.

(11)

В частности,

.

 

Пример 2.2.4. Уравнение с двумя переменными имеет решение . Определяет ли это уравнение неявную функцию в окрестности точки и если да, то найти и .

Обозначим . Имеем , , , , . Условие обеспечивает существование неявной функции , дифференцируемой в некоторой окрестности точки и согласно (10) имеем

.

В частности, .

Производную можно еще найти также следующим способом. Перепишем данное уравнение с учетом того, что есть функция от :

.

Тогда полная производная левой части этого равенства также равна нулю, т.е.

.

Отсюда

.

 

Неявная функция нескольких переменных

Функция называется неявной функцией переменных и , если она определяется уравнением , неразрешенным относительно .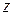

Теорема 2.2.4. Если дифференцируема по переменным , и 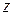в некоторой области и , то уравнение определяет однозначно неявную функцию , также дифференцируемую, и ее частные производные находятся по формуле

.

(12)

 

Пример 2.2.5. Найти и для неявной функции , определенной уравнением .

Способ 1, основанный на формулах (12). Найдем частные производные функции F:

, , .

Значит,

, ,

.

Способ 2 заключается в том, что если уравнение определяет неявную функцию , то имеем следующее тождество

,

,

.

Из первого тождества

,

из второго

.

 

Упражнения к §2.2.

1) Найти , если :

a)

b)

c)

d)

e)

f)

2) Для данных найти и :

a)

b)

c)

d)

e)

f)

3) Найти и для неявной функции , определяемой уравнением:

a)

b)

c)

 

ГЛАВА 3. ПРИМЕНЕНИЯ ЧАСТНЫХ ПРОИЗВОДНЫХ

 

§3.1. Производная по направлению. Градиент.

 

Случай двух переменных

Определение. Пусть – дифференцируемая функция в некоторой области , . Пусть – некоторое направление (вектор с началом в точке ), а – орт этого направления. Пусть – точка в направлении от . Обозначим . Тогда , . Предел отношения

называется производной функции по направлению .

Выражая этот предел через и , получаем

.

(13)

 

Теорема 3.1.1. Производная по направлению, касательному к линии уровня поверхности , равна нулю.

Случай нескольких переменных

По аналогии можно определить производную по направлению для функции трех переменных . Окончательная формула такова:

,

(14)

где – орт направления или – направляющие косинусы направления .

Теорема 3.1.2. Производная по направлению, касательному к линии уровня поверхности , равна нулю.

Градиент