Определение экстремума функции двух переменных в точке

Определение. Рассмотрим функцию двух переменных, определенную в некоторой области . Функция имеет локальный максимум (минимум) в точке , если неравенство ( ) имеет место во всех точках , достаточно близких к , но отличных от нее.

Теорема 3.3.1. (необходимые условия экстремума). Если дифференцируема в точке и имеет экстремум в этой точке, то ее дифференциал равен нулю:

(18)

Определение. Точка называется стационарной точкой функции , если .

Теорема 3.3.2 (достаточные условия экстремума). Пусть – стационарная точка функции . Обозначим

1. Если и , то —точка максимума.

2. Если и , то —точка минимума.

3. Если , то не является точкой экстремума.

4. Если , то точка может как быть, так и не быть точкой экстремума, поэтому требуется дополнительное исследование.

Пример 3.3.1 Исследовать на экстремум функцию .

Область определения — вся числовая плоскость , дифференцируема в каждой точке .

1. Определим стационарные точки (применим теорему 3.3.1).

Отсюда

Получили три стационарные точки:

2. Эти точки исследуем согласно теореме 3.3.2 на достаточность условий экстремума. Сначала определим отдельно

А теперь для каждой точки вычислим соответствующие , определим знаки величин и .

a) , т.е. не является точкой экстремума.

b) т.е. не является точкой экстремума.

c) . При этом . Вывод: — точка локального минимума функции с

Ответ:

Условный экстремум функции двух переменных

Определение. Под условным экстремумом имеется ввиду поиск экстремума некоторой функции при условии, что удовлетворяет некоторым условиям, описываемым уравнением (уравнение связи).

Чтобы найти экстремум функции при условии, что и связаны уравнением , необходимо составить вспомогательную функцию . Данная функция называется функцией Лагранжа, а – множителем Лагранжа. Координаты экстремальной точки должны удовлетворять трем уравнениям:

(19)

Из них и находятся .

Пример 3.3.2. Найти экстремум функции при условии, что и связаны уравнением .

Рассмотрим функцию Лагранжа . Имеем , . Из системы уравнений (19)

находим Нетрудно увидеть, что в точке функция достигает наибольшего значения .

Экстремум функции в области

Пусть функция определена и непрерывна в ограниченной замкнутой области . Тогда она достигает в некоторых точках своего наибольшего и наименьшего значений (т.е. глобальный экстремум). Эти значения достигаются функцией в точках, расположенных внутри области ., или в точках, лежащих на границе области.

Правило нахождения наибольшего и наименьшего значений дифференцируемой в области функции состоит в следующем:

1. Найти все критические точки функции, принадлежащие , и вычислить значения функции в них;

2. Найти наибольшее и наименьшее значения функции на границах области;

3. Сравнить все найденные значения функции и выбрать из них наибольшее и наименьшее .

Пример 3.3.3. Найти наибольшее и наименьшее значения функции в замкнутой области, ограниченной линиями: , , , (см. рис. 6).

Рисунок 6.

1. Здесь , . Находим все критические точки: Решением системы являются точки .

Ни одна из найденных точек не принадлежит области .

2. Исследуем функцию 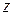на границе области, состоящей из участков .

На участке где ,

. Значения функции .

На участке , ,

. Значения функции .

На участке ,

. Значения функции .

На участке , ,

. Значения функции .

3. Сравнивая полученные результаты, имеем: .

Метод наименьших квадратов

Метод наименьших квадратов является непосредственным результатом применения исследования на экстремум функции нескольких переменных и заключается в следующем. На плоскости имеется система из точек Требуется подобрать некоторую функцию , которая «сглаживала» бы все точки этой системы, т.е. величина

(20)

Была бы минимальной; – квадрат отклонения ординаты функции в точке , от ординаты данной точки.

Рисунок 7.

В случае, если , речь идет о поиске прямой, квадратическое отклонение которой (см. рис.7) от данной системы точек было бы минимальным.

Существование минимума такой функции очевидно, поэтому соответствующие коэффициенты и прямой можно найти, используя только необходимые условия экстремума для функции двух переменных и :

(21)

Которые сводятся к линейной системе

(22)

где , , , , , .

Пример 3.3.4. Дана система точек, координаты которых указаны в таблице, число точек . Требуется построить прямую с уравнением , чтобы она отличалась как можно меньше от данной системы точек в смысле наименьших квадратов.

Для того, чтобы построить прямую, «сглаживающую» данные точки (они не лежат на одной прямой). Для этого достаточно решить систему уравнений (22). Для удобства расчетов строим рабочую таблицу

№
	-1	3,5 4,5			0,81 1,55 2,29 3,03 3,77 4,51	0,81 -0,45 -0,71 -0,47 0,77 0,01	0,6561 0,2025 0,5041 0,2209 0,5929 0,001
							2,1766

Первый столбец обозначает номер по порядку записи точек. Из сумм столбцов при составляются коэффициенты системы (22) для определения параметров и прямой . Система имеет вид:

Решим ее методом определителей (Крамера):

Искомое уравнение .

Упражнения к § 3.3.

1) Исследовать на экстремум следующие функции:

a) .

b) .

2) Исследовать на экстремум функцию в квадрате .

3) Исследовать на экстремум функцию в открытом квадрате .

4) Исследовать на экстремум неявную функцию , определяемую данным уравнением:

a)

b)

5) Найти наибольшее и наименьшее значения данной функции в данных замкнутых областях :

a)

b)

c)

6) Дана система точек, координаты которых указаны в таблице, число точек . Требуется построить прямую с уравнением , чтобы она отличалась как можно меньше от данной системы точек в смысле наименьших квадратов.

КОНТРОЛЬНАЯ РАБОТА

Вариант 1.

1. Найти полный дифференциал функции

2. Для функции , где , найти частные производные и .

3. Показать, что функция удовлетворяет уравнению

.

4. Вычислить приближенно .

5. Найти уравнение касательной плоскости и нормали к поверхности в точке .

6. Найти наибольшее и наименьшее значения производной по направлению функции в точке .

7. На эллипсе даны две точки и . На этом же эллипсе найти такую третью точку , чтобы треугольник имел наибольшую площадь (площадь треугольника выразить через координаты его вершин).

Вариант 2.

1. Найти полный дифференциал функции .

2. Найти частные производные и для функции , если .

3. Найти частные производные и для неявной функции , определяемой уравнением .

4. Вычислить приближенно изменение функции , если изменяется от 2 до 2,15, а изменяется от 1 до 1,25.

5. Составить уравнение касательной плоскости к поверхности , параллельной плоскости .

6. Показать, что функция удовлетворяет уравнению

.

7. Найти прямоугольный параллелепипед с длиной диагонали, равной , имеющий наибольший объем.

Вариант 3.

1. Найти частные и полное приращения функции в точке при

2. Найти , если , а .

3. Доказать, что функция удовлетворяет уравнению

.

4. Показать, что поверхности и имеют общую касательную плоскость в точке .

5. Найти точки разрыва функции .

6. Составить уравнение касательной плоскости и нормали к поверхности в точке .

7. На эллипсе найти точки наиболее и наименее удаленные от прямой .

Вариант 4.

1. Найти разность для функции в точке при .

2. Найти частные производные и для неявной функции , определяемой уравнением .

3. Показать, что функция удовлетворяет уравнению

.

4. Найти производную функции в точке (1;1) по направлению к точке (2;2). Найти также направления, по которым принимает наибольшее, наименьшее и равное нулю.

5. Вычислить предел .

6. Составить уравнение касательной плоскости и нормали к поверхности , параллельной прямой .

7. В полушар радиуса вписать прямоугольный параллелепипед наибольшего объема.

ТИПОВОЙ РАСЧЕТ

Вариант 1 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной прямыми

Вариант 2 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в квадрате, ограниченном прямыми

Вариант 3 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в круге

Вариант 4 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в треугольнике, ограниченном прямыми

Вариант 5 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в круге

Вариант 6 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в области

Вариант 7 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в области

Вариант 8 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в области

Вариант 9 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в круге

Вариант 10 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в области

Вариант 11 1. Дана функция . Показать, что . 2. Найти экстремумы функции . 3. Найти наименьшее и наибольшее значение функции в круге

Вариант 12 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в треугольнике

Вариант 13 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в прямоугольнике

Вариант 14 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной осями координат и прямой

Вариант 15 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в прямоугольнике с вершинами

Вариант 16 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной линиями

Вариант 17 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной прямыми

Вариант 18 1. Дана функция . Показать, что 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной линиями

Вариант 19 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной прямыми

Вариант 20 1. Дана функция . Показать, что . 2.Найти экстремумы функции . 3.Найти наименьшее и наибольшее значение функции в замкнутой области, ограниченной прямыми

Библиографический список

1. Пискунов С.П. Дифференциальное и интегральное исчисления. Том 1. М:Наука,1972, 456с.

2. Бугров С.А., Никольский С.М. Дифференциальное и интегральное исчисление. – М.Н.аука,1984.

3. Письменный Д.ТИ. Конспект лекций по высшей математике. 1 часть.–.

4. Лунгу К.Н., Письменный Д.Т., Федин С.Н., Шевченко Ю.А. Сборник задач по высшей математике. 1 курс.– М.:Рольф, 2001.–576с.

5. Гусак А.А. Справочное пособие по решению задач: математический анализ и дифференциальные уравнения.— Мн.:ТетраСимемс, 1998.–416с.

6. Щипачев В.С. Задачник по высшей математике: Учебн. пособие для вузов. – .М.:Высш. шк., 1998.–304с.

7. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в примерах и задачах. Часть 1. – М.: Высш. Шк., 1999.–304с.