Область гидравлически гладких труб

Цели работы

 

1. Экспериментально определить коэффициент сопротивления трения трубы.

2. Исследовать зависимость коэффициента сопротивления трения от числа Рейнольдса.

3. Построить характеристику трубы.

 

Общие сведения

 

Движение жидкости по трубопроводам сопровождается потерями напора (давления) [1, 2, 3, 4].

Торможение потока стенками трубы (в силу прилипаемости частичек жидкости к граничной поверхности) приводит к тому, что отдельные струйки жидкости движутся с различными скоростями относительно друг друга. В результате между слоями жидкости, а также между жидкостью и граничной поверхностью появляются касательные напряжения трения. Они, в общем случае, могут быть определены по формуле

 

,

 

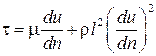где – коэффициент динамической вязкости жидкости;

– плотность жидкости;

– поперечный градиент скорости;

– длина пути смешения при турбулентном течении жидкости;

– касательное напряжение, обусловленное только вязкостью жидкости;

– турбулентное касательное напряжение, возникающее за счёт вихревого движения жидких частиц.

Внутренние силы трения создают сопротивление движению, на преодоление которого затрачивается часть механической энергии потока, переходящая в тепло. Поэтому удельная энергия потока по длине трубы уменьшается. Эта убыль удельной энергии (напора) называется потерей напора на трение по длине трубопровода .

Запишем уравнение Бернулли для горизонтального участка трубы длиной (плоскость сравнения проведена через ось трубы)

 

,

где , – пьезометрические напоры в выбранных сечениях трубы;

– средние скорости движения жидкости в этих сечениях;

– потери напора на участке трубы между выбранными сечениями.

В трубе постоянного сечения и тогда

 

,

 

т.е. потеря напора на трение равна убыли удельной потенциальной энергии потока и выражается разностью пьезометрических напоров в начальном и конечном сечениях данного участка трубы.

Расчёт потерь напора на трение при турбулентном режиме производится по формуле Дарси-Вейсбаха[2, 5]

, (1)

 

где – коэффициент сопротивления трения (коэффициент Дарси);

– длина трубы;

– диаметр трубы;

– средняя скорость потока жидкости,

– ускорение свободного падения.

Средняя скорость находится по формуле

 

, (2)

 

где – объемный расход жидкости в трубе;

– площадь сечения трубы.

Подставляя соотношения для средней скорости (2) и площади сечения, выраженной через диаметр трубы, в формулу (1), получаем:

 

или

. (3)

Зависимость (3) называется характеристикой трубы, а величина

 

(4)

 

именуется гидравлическим сопротивлением трубы.

Из выражения (4) следует, что сопротивление трубы зависит не только от геометрических размеров, но и от коэффициента сопротивления трения.

Экспериментально установлено, что коэффициент сопротивления трения в общем случае зависит от абсолютной шероховатости и диаметра трубы, скорости потока и кинематической вязкости жидкости. Эту зависимость можно представить в безразмерной форме

 

 

где – относительная шероховатость стенок трубопровода;

– число Рейнольдса.

Описать геометрию естественной абсолютной шероховатости (высоту и форму выступов неровности, их плотность) практически невозможно.

Поэтому вводится понятие эквивалентной шероховатости. Это такая однородная зернистая шероховатость (с одинаковой высотой выступов), для которой коэффициент Дарси в квадратичной области гидравлического сопротивления равен коэффициенту Дарси абсолютной шероховатости.

Эквивалентная шероховатость зависит от материала стенок, технологии обработки внутренней поверхности трубы, срока службы трубы, условий эксплуатации. Определяется экспериментальным путем в квадратичной зоне гидравлического сопротивления, приводится в справочниках.

Средние значения эквивалентной шероховатости для новых стальных цельнотянутых труб и бывших в употреблении (незначительно корродированных) .

Коэффициент сопротивления трения существенным образом зависит от режимов движения жидкости.

При ламинарном течении жидкости выступы шероховатости не участвуют в сопротивлении потоку. Потому коэффициент Дарси является функцией числа Рейнольдса , определяется для воды по формуле Пуазейля:

 

При числах Рейнольдса ламинарное течение жидкости переходит в турбулентное. Поскольку турбулентное течение потока жидкости начинает формироваться на оси потока, постепенно распространяясь к стенкам трубы, то у стенок трубы может сохраняться небольшой слой ламинарного течения жидкости, который называется ламинарной пленкой. Толщина последней может быть определена по формуле [2]

 

.

 

По мере увеличения скорости толщина ламинарной плёнки уменьшается. В зависимости от соотношения толщины ламинарной плёнки и величины абсолютной шероховатости (высоты выступов неровности) различают три области (зоны) гидравлического сопротивления, последовательно сменяющие друг друга с ростом скорости движения жидкости.

 

Область гидравлически гладких труб

В этой области толщина ламинарной плёнки значительно больше абсолютной шероховатости

.

 

Выступы шероховатости полностью затоплены в ламинарном слое, плавно обтекаются с очень малыми скоростями и не оказывают сопротивления потоку жидкости (рис. 1). Турбулентное ядро скользит по пристенному ламинарному слою. При этом коэффициент Дарси зависит только от числа Рейнольдса, т.е. .

Рис. 1. Структура потока в области
гидравлически гладких труб

Величина коэффициента сопротивления трения определяется по формуле

Блазиуса [2]

 

.

 

Границы области гидравлически гладких труб определяются неравенством

 

,

где - эквивалентная относительная гладкость стенок трубы.