Однозначность и эквивалентность грамматик
Сентенциальная форма грамматики.
Цепочка = 12 называется непосредственно выводимой из цепочки = 12 в грамматике G(VT,VN, P,S), V= VN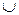 
VT,1, , 2 
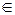V*, V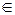+ , Если в грамматике G существует правило: 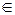P. Непосредственная выводимость цепочки из цепочки обозначается: =>. Из определения следует, что если взять несколько символов в цепочке и заменить их на другие символы согласно некоторому правилу грамматики и получить цепочку , то непосредственно выводима из .
Цепочка называется выводимой из цепочки (обозначается: =>* ), в том случае, если выполнено одно из двух условий:
1. непосредственно выводима из ( => );
2. существует такая , что выводима из и непосредственно выводима из ( =>* и => ).
Суть определения заключается в том, что => , то можно построить последовательность непосредственно выводимых цепочек от к , в которой каждая последующая цепочка непосредственно выводима из предыдущей цепочки. Такая последовательность называется выводом или цепочкой вывода.
Если цепочка вывода из к содержит одну и более промежуточных цепочек, она имеет специальное обозначение =>+ . Если количество шагов известно, можно его указать непосредственно у знака выводимости. Например, выражение =>3 означает, что выводится из за три вывода.
Вывод называется окончательным, если на основе цепочки , полученной в результате вывода, нельзя больше сделать ни одного шага вывода. Иначе говоря, вывод законченный, если цепочка, полученная в его результате пустая, либо содержит только терминальные символы грамматики.
Язык L, заданный грамматикой G(VT, VN, P,S) –это множество всех сентенциальных форм грамматики G. Язык L, заданный грамматикой G обозначается как L(G). Алфавитом языка L(G) будет множество терминальных символов грамматики VT, поскольку все конечные сентенциальные формы грамматики – цепочки над алфавитом VT. Тогда очевидно, что две эквивалентные грамматики должны иметь, по крайней мере, пересекающиеся множества терминальных символов. (Как правило, эти множества совпадают).
Вывод называется левосторонним, если в нем на каждом шаге вывода правило применяется к крайнему левому нетерминальному символу в цепочке. Аналогично, вывод называется правосторонним, если в нем на каждом шаге вывода правило применяется к крайнему правому нетерминальному символу в цепочке.
Примером левостороннего вывода является: S => Y => TY => TT => YTT => TTT, а правостороннего S => T => TX => T5 => T6. Вывод F => R является одновременно и лево- и правосторонним.
Встречаются выводы, которые нельзя отнести ни к левосторонним, ни к правосторонним, например TFT => TFFT => TFFF => FFFF => FFTFF.
Для грамматик типов 2 и 3 (КС-грамматик и регулярных грамматик) всегда можно построить левосторонний или правосторонний выводы. Для грамматик других типов это не всегда возможно, так как по структуре их правил не всегда можно выполнить замену крайнего левого или крайнего правого нетерминального символа в цепочке.
Деревом вывода грамматики G(VT,VN, P,S),называется граф, который соответствует некоторой цепочке вывода и удовлетворяет следующим условиям:
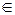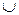каждая вершина графа обозначается некоторым символом грамматики А VN VT;
корнем дерева является вершина, обозначенная целевым символом грамматики S;
листьями дерева являются вершины, обозначенные терминальными символами грамматики или символом пустой цепочки 
,
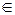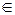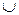если некоторый узел дерева обозначен нетерминальным символом A VN, а связанные с ним узлы – символами b, b2... bn; n > 0, 0 < i < n, bi (VN VT 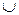{ }), то в грамматике G(VT,VN, P,S),существует правило А b1b2…bn 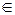Р.
Из определения следует, что по структуре правил дерево вывода в указанном виде всегда можно построить только для грамматик типов 2 и 3 (контекстно-свободных и регулярных). Для грамматик других типов дерево вывода в таком виде можно построить не всегда (либо же оно будет иметь несколько иной вид).
Для того чтобы построить дерево вывода, достаточно иметь только цепочку вывода. Дерево вывода можно построить двумя способами: сверху вниз и снизу вверх. Для строго формализованного построения дерева вывода всегда удобнее пользоваться строго определенным выводом: либо левосторонним, либо правосторонним.
При построении дерева вывода сверху вниз построение начинается с целевого символа грамматики, который помещается в корень дерева. Затем в грамматике выбирается необходимое правило, и на первом шаге вывода корневой символ раскрывается на несколько символов первого уровня. На втором шаге среди всех концевых вершин дерева выбирается крайняя (крайняя левая – для левостороннего вывода, крайняя правая – для правостороннего) вершина, обозначенная нетерминальным символом, для этой вершины выбирается нужное правило грамматики, и она раскрывается на несколько вершин следующего уровня. Построение дерева заканчивается, когда все концевые вершины обозначены терминальными символами, в противном случае надо вернуться ко второму шагу и продолжить построение.
Построение дерева вывода снизу вверх начинается с листьев дерева. В качестве листьев выбираются терминальные символы конечной цепочки вывода, которые на первом шаге построения образуют последний уровень (слой) дерева. На втором шаге в грамматике выбирается правило, правая часть которого соответствует крайним символам в слое дерева (крайним правым символам при правостороннем выводе и крайним левым при левостороннем). Выбранные вершины слоя соединяются с новой вершиной, которая выбирается из левой части правила. Новая вершина попадает в слой дерева вместо выбранных вершин. Построение дерева закончено, если достигнута корневая вершина (обозначенная целевым символом), а иначе надо вернуться ко второму шагу и повторить его относительно полученного слоя дерева.
Все известные языки программирования имеют нотацию записи «слева направо», компилятор также всегда читает входную программу слева направо (и сверху вниз, если программа разбита на несколько строк). Поэтому для построения дерева вывода методом «сверху вниз», как правило, используется левосторонний вывод, а для построения «снизу вверх» – правосторонний вывод.
Грамматика называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, можно построить единственный левосторонний (и единственный правосторонний) вывод. Грамматика также называется однозначной, если для каждой цепочки символов языка, заданного этой грамматикой, существует единственное дерево вывода. В противном случае грамматика называется неоднозначной.
Рассмотрим некоторую грамматику G ( {+, – , *, /, (, ), x, y}, {S}, P, S):
P: S S+S | S–S | S*S | S/S | (S) | x | y
Грамматика определяет язык арифметических выражений с четырьмя основными операциями: сложение, вычитание, умножение, деление и скобками.
Для цепочки, принадлежащей данному языку, x*y+x можно построить два варианта левостороннего вывода:
S => S+S => S*S+S => x*S+S => x*y+S => x*y+x
S => S*S => x*S => x*S+S => x*y+S => x*y+S
Каждому из этих вариантов будет соответствовать свое дерево вывода (рис. 1).
Рис. 1. Варианты дерева выражения x*y+x
Дерево вывода (или цепочка вывода) является формой представления структуры предложения языка. Поэтому для языков программирования, которые несут смысловую нагрузку, имеет принципиальное значение то, какая цепочка вывода будет построена для того или иного предложения языка. В рассмотренной грамматике все операции равноправны и для них не определен порядок выполнения. Поэтому с точки зрения арифметических операций приведенная грамматика имеет неверную семантику, хотя синтаксическая структура построенных с ее помощью выражений будет правильной. Такая ситуация вызывает неоднозначность в грамматике.
Если грамматика является неоднозначной, необходимо попытаться преобразовать ее в однозначный вид. Например, для рассмотренной грамматики арифметических выражений существует эквивалентная ей однозначная грамматика вида:
G’ ( {+, – , *, /, (, ), x, y}, {S, Т, Е}, P’, S):
P’: S S+T | S–T | T
T T*E | T/E | E
E (S) | x | y
Для арифметического выражения x*y+x в этой грамматике можно построить единственный левосторонний вывод:
S => S+T => T+T => T*E+T => E*E+T => x*E+T => x*y+T => x*y+E => x*y+x
На рис. 2 представлено единственно возможное дерево соответствующее этому выводу.
Рис. 2. Дерево вывода выражения x*y+x для однозначной грамматики
К сожалению, доказано, что не существует алгоритма, позволяющего проверить однозначность и эквивалентность грамматик. Однако, неразрешимость проблем эквивалентности и однозначности грамматик в общем случае не означает, что они не разрешимы вообще. Для многих частных случаев эти проблемы решены. Например, для КС-грамматик существуют правила определенного вида, по наличию которых во всем множестве правил грамматики G(VT, VN, P,S)можно утверждать, что она является неоднозначной. Эти правила имеют следующий вид:
1) А АА |
2) А АА |
3) А А | А |
4) А А | АА |
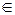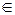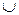здесь A VN; , , (VN VT)*.
Если в КС-грамматике встречается хотя бы одно правило любого из приведенных вариантов, то доказано, что такая грамматика точно будет неоднозначной. Однако если подобных правил во всем множестве правил грамматики нет, это совсем не означает, что грамматика является однозначной. То есть отсутствие правил указанного вида – необходимое, но не достаточное условие однозначности грамматики.
Существуют условия, при выполнении которых грамматика заведомо является однозначной. Они справедливы для всех регулярных и многих классов контекстно-свободных грамматик. Эти условия, напротив, являются достаточными, но не необходимыми для однозначности грамматик.
Контрольные вопросы
1. Что такое сентенциальная форма грамматики?
2. В чем заключается отличие левосторонних и правосторонних выводов?
3. В чем заключается однозначность грамматики?
4. Дайте определение полностью выводимой цепочки.
5. По каким правилам строится дерево вывода?
6. Выберите неверное утверждение:
а) однозначность – это свойство грамматики;
б) построение дерева вывода заканчивается, когда все концевые вершины обозначены терминальными символами;
в) проблема эквивалентности грамматик разрешима алгоритмически;
г) для того чтобы построить дерево вывода достаточно иметь только цепочку вывода.
Задание
1. Дана грамматика G({“ ”,i, f, t, h, e, n, l, s, b, a}, {E}, P,E)с правилами:
P: E if b then E else E; | if b then E; | a
Не строя цепочек вывода, показать, что грамматика является неоднозначной. Проверить это, построив некоторую цепочку вывода.
2. Построить эквивалентную ей однозначную грамматику.
3. Указать к какому типу относится каждая из грамматик языка десятичных чисел с фиксированной точкой:
3.1) G1 ({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, – , “.”}, {<число>, <цел>, <дроб>, <цифра>, <осн>, <знак>}, P1, <число>)
P1:
<число> <знак> <осн>
<знак> | + | -
<осн> <цел>. <дроб> | <цел>.
<цел> <цифра> | <цифра> <цифра>
<дроб> | <цел>
<цифра> <цифра> <цифра> <цифра> <цифра>
<цифра> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7| 8 | 9
3.2) G2 ({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, – , “.”}, {<число>, <часть>, <цифра>, <осн>}, P2, <число>)
Р2:
<число> +<осн>| -<осн> | <осн>
<осн> <часть>.<часть> |<часть>. |<часть>
<часть> <цифра> | <цифра> <цифра>
<цифра> <цифра> <цифра> <цифра> <цифра>
<цифра> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7| 8 | 9
3.3) G3 ({0, 1, 2, 3, 4, 5, 6, 7, 8, 9, +, – , “.”}, {<число>, <часть>, <осн>}, P3, <число>)
Р3:
<число> +<осн>| -<осн> | <осн>
<осн> <часть>. | <часть> | <осн>0 | <осн>1 | <осн>2 | <осн>3 | <осн>4 | <осн>5 | <осн>6 | <осн>7| <осн>8 | <осн>9
<часть> 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7| 8 | 9 | <часть>0 | <часть>1 | <часть>2 | <часть>3 | <часть>4 | <часть>5 | <часть>6 | <часть>7| <часть>8 | <часть>9
4. Определить является ли однозначной каждая из грамматик, описанная в задание 3.
5. Построить цепочки вывода для цепочек -57, 196, 11.9 но основе грамматик из задания 3.
6. Перестроить грамматики, определенные в задании 3 таким образом, чтобы они допускали цепочки вида: .124, .34.