Коэффициенты турбулентной диффузии (Dтурб) в морях

Й закон Фика

 
 

 
 
(5.5.1))

 


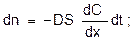Й закон Фика

 
 

 
 
(5.5.2)

 


где n – количество диффундирующего вещества, S – сечение, перпендикулярное потоку вещества, t – время, C – концентрация диффундирующего вещества, D – коэффициент диффузии, x – координата в направлении диффузии.
Какую роль играет диффузия в рассеянии загрязняющих веществ (ЗВ) в объектах окружающей среды?

Коэффициенты диффузии загрязнителей в различных средах могут быть найдены в справочниках или рассчитаны по уравнению Эйнштейна:

 
 

 
 
(5.5.3)

 


где R – универсальная газовая постоянная, A – число Авогадро, h – вязкость среды, r – радиус диффундирующей частицы, T – абсолютная температура.

Уравнение (5.5.3) выведено для коллоидных систем, однако для приближенной оценки коэффициентов диффузии его можно применять и для истинных растворов.

–
Эйнштейн и Смолуховский показали также, что в коллоидных растворах среднее смещение частиц (Dx) можно найти из выражения:

 
 

 
 
(5.5.4)

 


По уравнению (5.5.4) можно приближенно рассчитывать среднее смещение границы загрязнения в различных средах за определенный промежуток времени, а по уравнению:

 
 

 
 
(5.5.5)

–
находить время прохождения фронтом загрязнителя пути Dx.

Точные расчеты переноса загрязнителей от точки выброса можно провести, решив уравнение (5.5.2). Однако это уравнение не имеет общего решения, а может быть решено лишь при определенных граничных условиях.

Если имеется постоянный выброс загрязнителя, концентрация которого в выбросе постоянна и равна C0, а концентрация C в начальный момент в любых точках, кроме точки выброса, равна нулю, то граничные условия имеют вид:

1) C=0 при t=0; 2) при x=0, C=C0=const и не зависит от времени.

Решение уравнения (5.5.2) при этих граничных условиях имеет вид:

 
 

 
 
(5.5.6)

 


где второй член, стоящий в скобках, – интеграл вероятностей (трансцендентная функция Крампа), определяемый по специальным таблицам (табл. 5.5.10).

Естественно, что отсутствие перемешивания (ветра, течений и т.п.) в природных средах – явление достаточно редкое, поэтому и расчеты по уравнению (5.5.6) с использованием коэффициентов молекулярной диффузии имеют ограниченное значение. На практике применяются другие, значительно более сложные расчеты, приводимые далее.

Таблица 5.5.10

 
 

Интеграл вероятностей (трансцендентная функция Крампа)

 

 

z F z F z F
0,01 0,01128 0,65 0,64203 1,80 0,98909
0,02 0,70 1,85
0,03 0,75 1,90
0,04 0,80 1,95
0,05 0,85 2,00
0,06 0,90 2,05
0,07 0,95 2,10
0,08 1,00 2,15
0,09 1,05 2,20
0,10 1,10 2,25
0,13 1,15 2,30
0,17 1,20 2,35
0,20 1,25 2,40
0,23 1,30 2,50
           

 

z F z F z F
0,27 1,35 2,60
0,30 1,40 2,70
0,33 1,45 2,80
0,37 1,50 2,85
0,40 1,55 2,90
0,45 1,60 3,00
0,50 1,65 3,07
0,55 1,70 3,23 1,00000
0,60 1,75    

 

. Диффузия в почве и донных осадках

Почва и донные осадки, в принципе, – твердые фазы, поэтому в них перемешивание практически всегда отсутствует. Следовательно, рассеяние загрязнителей в этих средах должно строго описываться уравнением (5.5.6) с использованием молекулярных коэффициентов диффузии.

Согласно большому массиву экспериментальных данных, молекулярные коэф-фициенты диффузии различных веществ в газовой фазе составляют примерно n×10–1 см2/с, в жидкой – n×10–5 см2/с, а в твердой фазе – n×10–10 см2/с.

В соответствии с этим, согласно уравнению (5.5.4), среднее смещение границы загрязнения за несколько суток в атмосфере будет определяться метрами, в водной среде – сантиметрами, а в почвах и донных осадках – долями миллиметров.

Однако реально почвы часто, а донные осадки никогда не являются истинными твердыми фазами, так как первые часто, а вторые всегда содержат воду, то есть являются влажными. Эта вода находится в порах и трещинах твердых фаз, и в этой жидкой составляющей почв и донных осадков диффузия загрязнителей протекает со скоростями, которые определяются коэффициентами диффузии в жидкостях, на несколько порядков большими, чем коэффициенты диффузии в твердой фазе.

Поэтому коэффициент диффузии, не реагирующей с твердой основой загрязнителя в осадке или почве, определяется по уравнению:

 
 

 
 
(5.5.7)

 


где D – коэффициент диффузии загрязнителя в осадке или почве, D0 – коэффициент диффузии в свободном растворе, наполняющем осадок, j – пористость и q – извилистость осадка, или по уравнению:

 
 

 
 
(5.5.8)

 


где LS – электропроводность водонасыщенного осадка, LW – электропроводность поровой воды.

Так как электропроводность экспериментально определяется проще и быстрее, чем пористость и извилистость, использование уравнения (5.5.8) часто более предпочтительно.

Отношение LW/LS для морских глубоководных осадков обычно лежит в пределах от 1,6 до 13,6.

5.5.2.3. Рассеяние загрязнителей из дымовых труб

Распространение выходящего из труб газа в атмосфере определяется аэродинамикой самой нижней части атмосферы. Потоки воздуха у поверхности земли могут быть турбулентными или ламинарными.

В солнечный день почва и воздух вблизи нее теплее верхних слоев воздуха, поэтому поднимающиеся потоки теплого воздуха поддерживают атмосферу в состоянии турбулентности.

В ясную ночь земля охлаждается быстрее, и холодный воздух вблизи земли плохо перемешивается с более теплыми верхними слоями, ветер у земли стихает. В период зимнего антициклона, особенно когда дым или туман ослабляют солнечное тепло, такое устойчивое состояние может наблюдаться в течение всего дня.

В облачную погоду солнечная радиация минимальна, и температурный градиент становится нейтральным или адиабатическим. Температура воздуха с высотой падает за счет охлаждения поднимающегося воздуха при адиабатическом расширении. Турбулентность в воздухе зависит от ветра и рельефа земли.

На рис. 5.5.2 показано рассеяние дыма из трубы (в средней части), изменение температуры воздуха (слева) и концентрации загрязнителя (справа) с высотой.

Штриховой линией показано адиабатическое изменение температуры. В случае «а» температура падает быстрее, чем при адиабатическом изменении. Такое состояние называется переходным. В случае «б» температура растет с высотой, это состояние называется инверсией. Случай «в» является вариантом, когда нижняя часть струи находится в состоянии инверсии, а верхняя – в переходном состоянии.

Концентрация загрязнителя во всех случаях максимальна в центре струи и уменьшается к периферии, особенно резко в состоянии инверсии.

В переходном состоянии на струе могут наблюдаться «пучности» (как вверх, так и вниз), вызванные турбулентностью в нестабильных условиях. В условиях инверсии струя не размывается.

 
 

Рис. 5.5.2. Рассеяние дыма из трубы (обозначения в тексте)

Рис. 5.5.3. Зависимость концентрации загрязнителя на уровне земли от расстояния от трубы

 

Изменение концентрации загрязнителя на уровне земли (1 м от земли) в зависимости от расстояния от трубы показано на рис. 5.5.3. Максимальная концентрация наблюдается на расстоянии, равном 10–30 высотам трубы.

Если температура выбрасываемого из трубы газа значительно выше температуры окружающего воздуха, над трубой наблюдается восходящий столб дыма и вместо истинной высоты трубы следует брать эффективную высоту, которая учитывает этот эффект.

Кроме того, на рассеяние загрязнителей из дымовых труб влияет характер рельефа местности и высота строений и сооружений в окрестностях трубы, за счет которых может происходить размыв струи, подсос дыма в низины или пространства между зданиями, возникновение застоя загрязнителя в складках местности и между строениями.

В адиабатических и переходных условиях расчет концентрации загрязнителя на уровне земли с достаточной точностью можно провести по уравнению Саттона, полученному теоретически и проверенному на распространении радиоактивного изотопа аргона, дыма, масляного тумана и оксида серы (IV):

 
 

 
 
(5.5.9)

 


где C(x) – концентрация загрязнителя на расстоянии x м, ед. выд./м3; h – высота трубы, м; Q – скорость (мощность) выброса, ед. выд./с; v – скорость ветра, м/с; Dy и Dz – фактические коэффициенты диффузии в горизонтальном и вертикальном направлениях; n – безразмерный параметр, зависящий от устойчивости потока.

Имеется также более сложное уравнение, учитывающее рассеяние загрязнителя в направлении, перпендикулярном потоку дыма.

Приложение 5.5.1

Коэффициенты молекулярной диффузии (D)

а) В воздухе, см2/с

 

Вещество Температура, оC D
NH3 0,227
SO2 0,122
COCl2 0,095
CO2 0,138
Бензин 0,091
J2 0,081
HCN 0,173
Cl2 0,124
Ацетон 0,109
Rn 0,120

 


Приложение 5.5.2

Коэффициенты турбулентной диффузии (Dтурб) в морях

Масштаб длины, км 0,1 1,0 10,0
Dтурб, см2/с 103 104 (3–5)×105

 

Приложение 5.5.3

Параметры при расчете выбросов из дымовой трубы (уравнение (5.9))

Безразмерный параметр n=0,25.

Фактические коэффициенты диффузии:

Dy=Dz=0,12 при h>100 м,

Dy=Dz=0,25 при h<100 м.

 

5.5.3. Решение типовых заданий

Задание 5.5.3.1.

%
Рассчитать среднее смещение границы загрязнения атмосферы при залповом выбросе аммиака за 1 сут при 20оC за счет молекулярной диффузии.

Решение:

 
 

В приложении 5.5.1 находим коэффициент молекулярной диффузии аммиака в воздухе (D=0,227 см2/с) и, используя уравнение (5.4), находим

Задание 5.5.3.2.

%
Какая доля от исходной концентрации аммиака, остающейся постоянной за счет непрерывного выброса, будет наблюдаться за счет молекулярной диффузии через 10 сут после начала его сброса на расстоянии 10 м при 20оC?

Решение:
Коэффициент диффузии аммиака найден при решении предыдущей задачи.

Согласно (5.6),

 

 
 

На основе условий задачи находим верхний предел интегрирования


Затем находим значение интеграла, стоящего в скобке в (5.5.6), и подставляем его в эту формулу: C/C0=1–0,89, отсюда C/C0=0,11.

Примечание. Возможны многочисленные задачи этого типа: если дано числовое значение C0, то можно вычислить конкретное значение C; могут быть даны значения C и C0 (например, C=ПДК), а найти требуется x или t, тогда из отношения C/C0 находят значение интеграла.

Задание 5.5.3.3.

%
Через какое время в турбулентных условиях при непрерывном сбросе в водоем загрязнителя его концентрация на расстоянии 10 км составит 10% от концентрации в месте сброса?

Решение:

Коэффициент турбулентной диффузии при масштабе 10 км равен 4 ×105 см2/с в среднем.

Из условий задачи и (5.5.6) C/C0=0,1=(1–0,9), т.е. интеграл вероятностей равен 0,9, а верхний предел интегрирования равен 1,17, поэтому

 
 

 


откуда

 

t=(675,7)2:(24×3600)=5,3 суток.


Примечание. Как и для предыдущей задачи, возможны различные варианты условий. Принципы решения не отличаются от указанных там же. Коэффициенты турбулентной диффузии следует выбирать в соответствии с масштабами расстояния.

5.5.4. Задания для самостоятельного решения

Задание 5.5.4.1.

%
Рассчитать среднее смещение границы загрязнения водоема за счет молекулярной диффузии при залповом выбросе соляной кислоты за 1 и 30 сут при 25 оC.