Решение. Векторное и смешанное произведения векторов

Векторное и смешанное произведения векторов.

 

Три некомпланарных вектора 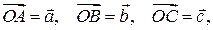взятые в указанном порядке и приложенных в одной точке называются тройкой векторов .

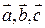Если при наблюдении из конца вектора кратчайший поворот от к происходит против часовой стрелки, то тройка векторов 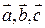называется правой, если указанный поворот совершается по часовой стрелке, тройка 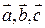называется левой.

 

правая тройка левая тройка

 

Векторным произведением векторов и называется вектор , обозначаемый , который удовлетворяет следующим трём условиям:

1.

2.

3. образуют правую тройку векторов.

Свойства векторного произведения:

Если векторы и заданы своими координатами: и ,

то их векторное произведение может быть вычислено по формуле .

Пример 1. Даны векторы Найти координаты векторного произведения

Решение.

----------------------------------------------------------------------------------------------------------------

Векторное и смешанное произведения векторов. Стр. 1

Геометрический смысл векторного произведения. Площадь S параллелограмма, построенного на векторах и , имеющих общее начало, вычисляется по формуле: .

Площадь треугольника соответственно:

Пример 2. Вершины треугольника находятся в точках A(1;1;3), B(3;-1;6); С(5;1;-3). Вычислить его площадь.

Решение. Выберем два вектора, выходящих из одной вершины. Например, и . Определим координаты выбранных векторов:

; .

Вычислим векторное произведение найденных векторов:

Найдём модуль полученного вектора:

.

Тогда площадь треугольника равна (кв.ед.).

Механический смысл векторного произведения. Вращающий момент силы , приложенной к точке B тела, закреплённого в точке A, вычисляется по формуле .

Пример 3. Точка N(2,3,4) твёрдого тела закреплена. В точке Q(0,3,4) приложена сила . Найти момент силы относительно точки N.

Решение. Момент силы можно вычислить с помощью формулы .

Определим координаты вектора : . Тогда вращающий момент равен .

 

С помощью векторного произведения можно найти: 1) вектор, который перпендикулярен двум данным векторам; 2) площадь параллелограмма (треугольника); 3) вращающий момент силы.

Смешанным произведением векторов 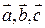называется число, которое вычисляется по формуле

Свойства смешанного произведения:

(признак компланарности)

----------------------------------------------------------------------------------------------------------------

Векторное и смешанное произведения векторов. Стр. 2

Если векторы , и заданы своими координатами: , , , то их смешанное произведение может быть вычислено по формуле

Геометрический смысл смешанного произведения. Объём параллелепипеда, построенного на векторах 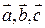равен: .

Объём пирамиды: .

Пример 4. Найти объём параллелепипеда, построенного на векторах .

Решение. Вычислим смешанное произведение векторов:

Тогда объём параллелепипеда равен (куб.ед.).

 

С помощью смешанного произведения можно: 1) вычислить объём параллелепипеда (пирамиды); 2) выяснить, являются ли векторы компланарными.