III.Методика измерений и расчетные формулы. I.Цель работы: ознакомление с принципом работы баллистического крутильного маятника; определение скорости полета пули

ЛАБОРАТОРНАЯ РАБОТА № 1.8

«ИЗУЧЕНИЕ ЗАКОНОВ СОХРАНЕНИЯ ЭНЕРГИИ И

МОМЕНТА ИМПУЛЬСА С ПОМОЩЬЮ БАЛЛИСТИЧЕСКОГО МАЯТНИКА»

I.Цель работы: ознакомление с принципом работы баллистического крутильного маятника; определение скорости полета пули, попавшей в него.

II.Описание установки.

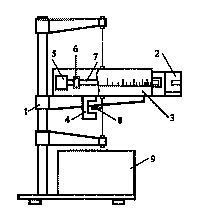
Общий вид баллистического крутильного маятника представлен на рисунке. К кронштейну 1 прикреплены: стреляющее устройство 2, прозрачный экран с нанесенной на него угловой шкалой 3 и фотоэлектрический датчик 4. Маятник состоит из двух мисочек, наполненных пластилином 5, двух перемещаемых грузов 6, двух стержней 7 и заслонки 8.

Если освободить пулю от стреляющего устройства, то она вклеится в пластилин, находящийся в мисочках крутильного маятника, и вызовет отклонение последнего на некоторый угол от положения равновесия. Кинетическая энергия маятника, полученная им от пули, постепенно будет переходить в потенциальную энергию упругой деформации закручивающейся нити.

Затем начнется процесс перехода потенциальной энергии в кинетическую и т.д. Маятник будет совершать гармонические крутильные колебания, период которых значительно больше времени соударения.

Угол отклонения маятника считывают с угловой шкалы 3. Число колебаний и время определяется миллисекундомером 9.

III.Методика измерений и расчетные формулы

Систему пуля - маятник можно считать замкнутой. Применим к ней закон сохранения момента импульса:

где 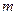и - масса и скорость пули соответственно; r - расстояние от оси вращения маятника до центра масс пули в месте ее вклеивания; J_n - момент инерции пули относительно оси вращения маятника; J - момент инерции маятника при некотором расположении грузов на нем; - начальная угловая скорость маятника.

Поскольку J_n << J, то

. (1)

Из (1) следует, что для определения скорости пули необходимо найти момент инерции и начальную угловую скорость маятника, т.к. величины m и r могут быть непосредственно измерены.

Дня определения воспользуемся законом сохранения механической энергии и основным законом динамики для вращательного движения.

Маятник будет совершать колебания под действием упругого момента нити, пропорционального углу поворота маятника :

М = - ,

где k - коэффициент пропорциональности (модуль кручения). Знак "-" указывает на то, что вектор момента силы направлен в сторону, противоположную направлению вектора отклонения маятника.

Элементарная работа против сил упругости по закручиванию нити на малый угол равна

После интегрирования получаем, что .

Если пренебречь незначительными потерями на трение, то можно записать:

или , (2)

где - максимальный угол отклонения маятника от положения равновесия.

По закону динамики для вращательного движения

или .

Частным решением этого уравнения является

в чем можно убедиться непосредственной подстановкой.

Величина - в последнем выражении является циклической частотой колебаний, которая по определению равна .

Таким образом, маятник будет совершать гармонические колебания с периодом

. (3)

Подставив в формулу (3) выражение для из формулы (2), получим следующее выражение для начальной угловой скорости маятника:

. (4)

Если на стержне маятника закреплены 2 груза, причем расстояние R₁, от оси маятника до центра масс каждого груза значительно больше размеров груза, то момент инерции системы будет равен

, (5)