Nombre:__________________________________________________________
EXAMEN DE SEGUNDA EVALUACIÓN DE CONTROL AUTOMATICO
Primer tema: 35 puntos
Si Gc(s) = K , 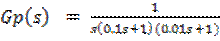 , H(s) =1
a) Dibuje el gráfico asintótico de Bode de la ganancia de lazo GcGpH(s), para la ganancia logarítmica y la fase con la ganancia K ajustada para un Margen de fase de 45o.
b) Para los siguientes valores de w = 0.5, 1, 2, 5, 10, 20, traslade el gráfico de la ganancia de lazo a la carta de Nichols, determine el margen de ganancia.
|
c) A partir de la carta de Nichols, determine en Bode la respuesta de frecuencia de magnitud de lazo cerrado, la frecuencia de resonancia wr y el valor máximo Mpw
|
Segundo Tema: 30 puntos
Si Gc(s) = K ,  , H(s) =1
a) Si K = 1, construya el gráfico polar, considere en su gráfico los siguientes valores de frecuencia w = 0, 0.5, 1, 1.5 e infinito. Además el punto de cruce de ganancia y el punto de cruce de fase, el Margen de Ganancia y el Margen de Fase.
| b) Si se añade un compensador de retardo de fase  construya el gráfico de Bode del sistema compensado y determine cuál es el efecto de este compensador.
c) Compare los valores de Kv sin compensador y con compensador
|
Tercer tema: 35 puntos.
Si Gc(s) = K ,  , H(s) =1
a) Bosqueje la trayectoria de las raíces del sistema sin compensar.
b) Diseñe un compensador de adelanto de fase para cumplir con las siguientes especificaciones para las raíces complejas: S.P. = 7.5% y tiempo de estabilización de 400 milisegundos. Ubique el cero del compensador en s = -15 y determine la ubicación del polo del compensador
| c) Determine mediante el criterio de magnitud el valor de K en la ubicación deseada y de allí el valor de Kv.
d) Bosqueje la trayectoria de las raíces del sistema compensado, verifique que se cumplen los requerimientos para la respuesta transiente.
|