отчет о лабораторной работе

ИНСТИТУТ УПРАВЛЕНИЯ БИЗНЕС ПРОЦЕССАМИ И ЭКОНОМИКОЙ

Факультет Прикладной экономики и управления экономическими системами

Кафедра Экономики и управления

Дисциплина Статистика

Группа ПЭ 09-01

отчет о лабораторной работе

Преподаватель Боровкова О. Г.

Разработал студент Бородулина К.Ю.

Красноярск, 2010 г.

Цель работы:

Закрепить полученные теоретические данные и практические навыки по расчету и анализу основных статистических показателей.

Теоретическое введение

Наиболее распространенной формой статистических показателей, используемой в социально-экономических исследований, является средняя величина. Она представляет собой обобщенную количественную характеристику признака в статистической совокупности в конкретных условиях места и времени. Показатель в форме средней величины выражает типичные черты и дает обобщенную характеристику однотипных явлений по одному из варьирующих признаков. Он отражает уровень этого признака, отнесенный к единице совокупности.

Важнейшее свойство средней заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. Значения признака отдельных частиц совокупности могут колебаться в ту или иную сторону под влиянием множества факторов, среди которых могут быть как основные, так и случайные.

Сущность средней в том и заключается, что в ней взаимопогашаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием факторов основных. Это позволяет средней отражать типичный уровень признака и абстрагироваться от индивидуальных особенностей, присущих отдельным единицам.

Типичность средней непосредственным образом связана с однородностью статистической совокупности. Средняя величина только тогда будет отражать типичный уровень признака, когда она рассчитана по качественно однородной совокупности.

Наиболее распространенным видом средних величин является средняя арифметическая, которая, как и все средние, в зависимости от характера имеющихся данных может быть простой или взвешенной.

Средняя арифметическая простая. Эта форма средней используется в тех случаях, когда расчет осуществляется по не сгруппированным данным.

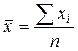(1)

Средняя арифметическая взвешенная. При расчете средних величин отдельные значения осредняемого признака могут повторяться, встречаться по несколько раз. В подобных случаях расчет производится по сгруппированным данным или интервальными.

Расчет производится по формуле арифметической взвешенной:

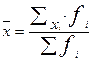(2)

Для характеристики структуры совокупности используются такие показатели как мода и медиана, называемые структурными или распределительными средними.

Модой (Мо) называется наиболее часто встречающийся вариант или то значение признака, которое соответствует максимальной точке теоретической кривой распределения.

В дискретном ряду мода – это вариант с наибольшей частотой. В интервальном вариационном ряду модой приближенно считают центральный вариант так называемого модального интервала.

Модальный интервал – интервал, который имеет наибольшую частоту (частость).

Конкретное значение моды для интервального ряда определяется формулой:

, (3)

где х_мо – нижняя граница модального интервала;

i_мо – величина модального интервала;

f_мо – частота, соответствующая модальному интервалу;

f_мо-1– частота интервала, предшествующая модальному интервалу;

f_мо+1– частота интервала, следующего за модальным.

Медиана (М_е) - это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значение варьирующего признака меньше, чем средний вариант, другая большие.

В дискретном ряду с четным числом индивидуальных величин медианой будет средняя арифметическая из двух смежных вариант, а с нечетным числом медианой будет варианта, расположенная в центре ряда.

Для интервального ряда медиана определяется по формуле:

(4)

где х_ме- нижняя граница медианного интервала;

i_ме - величина медианного интервала;

s_ме-1– сумма частот, накопленная до медианного интервала;

f_ме – частота, соответствующая медианному интервалу.

Медианный интервал – первый интервал, в котором накопленная частота составляет половину или больше половины общей суммы частот. Рассматривая зарегистрированные в процессе статистического наблюдения величины того или иного признака у отдельных единиц совокупности можно обнаружить между ними различия. Колеблемость, многообразие, изменяемость величины признака у единиц совокупности называются вариацией. Вариация порождается комплексом условий, действующих на совокупность ее единицы.

Исследование вариации в статистике дает возможность оценить степень воздействия на данный признак других варьирующих признаков. Определение вариации необходимо при организации выборочного наблюдения, построении статистических моделей, разработке материалов экспертных опросов и во многих других случаях.

Наличие вариации в признаках изучаемых явлений ставит перед статистикой задачи ее исследования: определение меры вариации, ее измерение, нахождение соответствующих измерителей, показателей, характеризующих ее размеры, выявление их сущности и методов вычисления факторов, ее определяющих.

По степени вариации можно судить о многих сторонах процесса развития изучаемых явлений, в частности об однородности совокупности, устойчивости индивидуальных значений признака, типичности средней, о взаимосвязи между признаками одного и того же явления и признаками разных явлений. Статистические показатели, характеризующие вариацию, широко применяются в практической деятельности.

Показатели вариации делятся на две группы: абсолютные и относительные. К абсолютным относятся размах вариации, среднее линейное отклонение, дисперсия и среднее квадратическое отклонение. Вторая группа показателей вычисляется как отношение абсолютных показателей вариации к средней арифметической. Относительными показателями вариации являются коэффициенты осцилляции, вариации, относительное линейное отклонение и др.

Самым простым абсолютным показателем является размах вариации (R).

Размах показывает, насколько велико различие между единицами совокупности, имеющими самое маленькое и самое большое значение признака.

Его рассчитывают как разность между наибольшим (х_max) и наименьшим (x_min) значениями варьирующего признака, т.е.

(5)

Размах вариации – важный показатель колеблемости признака но не исчерпывающий его характеристику.

Для анализа вариации необходим и показатель, который отражает все колебания варьирующего признака, дающий обобщенную ее характеристику. Для многих варьирующих признаков возможно допущение, что при прочих равных условиях все единицы совокупности в соответствии с основными законами своего развития имели бы одинаковую и притом вполне определенную величину признака в данных условиях места и времени. Вполне логично в качестве такой величины условно принять среднюю величину из всех значений признака, поскольку в ней более или менее погашаются случайные отклонения от закономерного хода развития явления, и средняя тем самым отражает типичный размер признака у данной однородной совокупности единиц. Но условия существования и развития отдельных единиц совокупности в определенной степени различны, что сказывается и на различии значений у них взятого нами признака. Средняя величина отражает эти средние условия.

Следовательно, средняя применяется в качестве своего рода центра тяжести, вокруг которого происходит колебание, рассеяние значений признака. При обобщении этих колебаний необходимо вновь прибегнуть к методу средних величин – найти среднюю величину этих отклонений.

Такая средняя называется средним линейным отклонением (d). Оно вычисляется как средняя арифметическая из абсолютных значений отклонений вариант и (взвешенная или простая в зависимости от исходных условий) по следующим формулам:

(простая), (6)

(взвешенная) (7)

Поскольку сумма отклонений значений признака от средней величины равна нулю, приходится все отклонения брать по модулю, приходится все отклонение брать по модулю, на что указывают прямые скобки в числителе формул.

Среднее линейное отклонение дает обобщенную характеристику степени колеблемости признака в совокупности. Однако при его исчислении приходится допускать некорректные с точки зрения математики действия, нарушать законы алгебры, что побудило математиков и статистиков искать иной способ оценки вариации для того, чтобы иметь дело только с положительными величинами. Самый простой выход – возвести все отклонения во вторую степень. Это столь простое решение привело к большим научным результатам. Оказалось, что обобщающие показатели вариации, найденные с использованием вторых степеней отклонений, обладают замечательными свойствами. Поэтому они получили широкое распространение в различных областях знаний, на их основе были разработаны новые методы исследования, а также новые показатели количественной характеристики большого класса явлений.

Полученная мера вариации называется дисперсией (2), а корень квадратный из дисперсии – средним квадратическим отклонением (). Эти показатели являются общепринятыми мерами вариации и часто используются в статистических исследованиях, а также в технике, биологии и др. отраслях знаний. Данные показатели нашли также свое широкое применение в международной практике учета и статистического анализа, в частности в системе национального счетоводства.

Дисперсия представляет собой средние квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсии (в зависимости от исходных данных):

(простая дисперсия) (8)

(взвешенная дисперсия) (9)

Дисперсия – средняя величина квадратов отклонений. В данном случае варианты признака выражены в первой степени, значит, и мера их вариации также должна быть взята в первой степени. Для этого достаточно извлечь из дисперсии корень второй степени, получится среднее квадратическое отклонение (). Значит, среднее квадратическое отклонение равно корню квадратному из дисперсии:

(10)

(11)

Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единица измерения, что и признак (в метрах, тоннах, рублях, процентах и т.д.)

До сих пор говорилось о показателях вариации, выраженных в абсолютных величинах. Но для целей сравнения колеблемости различных признаков в одного и того же признака в нескольких совокупностях представляют интерес показатели вариации, приведенные в относительных величинах. Базой для сравнения должна служить средняя арифметическая. Эти показатели вычисляются как отношение размаха вариации, среднего линейного отклонения или среднего квадратического отклонения к средней арифметической или медиане. Чаще всего они выражаются в процентах и определяют не только сравнительную оценку вариации, но и дают характеристику однородности совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33% (для распределений, близких к нормальному). Различают следующие относительные показатели вариации:

Коэффициент осцилляции (Ко):

(12)

Линейный коэффициент вариации ( ):

(13)

Наиболее часто в практических расчетах применяется показатель относительной вариации – коэффициент вариации.

Коэффициент вариации (К или V):

(14)

Практическая часть

1) Определение средних величин и показателей вариации по несгруппированным данным

В исходных данных представлена информация о количестве единиц приобретаемого товара.

По формулам простой средней арифметической (1), медианы для дискретного ряда, среднего линейного отклонения (6) и дисперсии (8) определим статистические показатели, результаты расчетов представлены в таблице 2. Для нахождения данных показателей использованы стандартные функции Excel:

· СРЗНАЧ – нахождение среднего значения (по несгруппированным данным);

· МЕДИАНА – расчет медианы дискретного ряда;

· СРОТКЛ – определение среднего линейного отклонения;

· ДИСП – оценка дисперсии;

· СТАНДОТКЛОН – вычисление среднеквадратического отклонения.

2) Определение средних величин и показателей вариации по сгруппированным данным

По результатам группировки по количеству единиц приобретаемого товара, подготовленной в лабораторной работе №1 имеем следующие данные интервального ряда (таблица 1).

Таблица 1 – Вспомогательная таблица для расчета

Группы банков	Середина интервала (х_i')	Кол-во банков (f_i)	х_i'*f_i	\|х_i'-x_ср\|*f_i	(х_i'-x_ср)²*f_i	Накопленные частоты (s_i)
начало	конец
						41 999
						19 367
						80 101
					1 715	154 847
						66 894
						20 245
						24 389
Итого				4 506	407 842

Среднее значение признака характеризуют показатели:

а) средняя арифметическая (взвешенная):

б) мода

в) медиана

Определим абсолютные показатели вариации:

а) размах вариации

б) среднее линейное отклонение

4,284902581

в) дисперсия

36,30595173

г) среднеквадратическое отклонение

6,025442036

Вычислим относительные показатели вариации:

а) коэффициент осцилляции

1,183536694

б) линейный коэффициент вариации

0,28174108

в) коэффициент вариации

0,396185097

Таблица 2 – Статистические показатели

Показатели	Значение
дискретный ряд	интервальный ряд
Средняя арифметическая	10,02	15,208654
Мода	–	22,12766
Медиана		10,539425
Размах вариации
Среднее линейное отклонение	3,1048	4,2849026
Дисперсия	17,81592	36,305952
Среднее квадратическое отклонение	4,220891	6,025442
Коэффициент осцилляции	1,796407	1,1835367
Линейный коэффициент вариации	0,30986	0,2817411
Коэффициент вариации	0,421247	0,3961851

Выводы

Закрепили полученные теоретические данные и практические навыки по расчету и анализу основных статистических показателей.

Сравнивая значения дискретного ряда и интервального, можно сказать, что величины приблизительно равны между собой.