Свойства высот треугольника
Планиметрия. Тема 1. Углы треугольника. Тригонометрические функции углов. Решение треугольников.
Виды треугольников 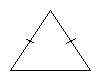
Треугольник называется равнобедренным, если у него две стороны равны. Эти равные стороны называются боковыми сторонами, а третья сторона называется основанием треугольника.
Треугольник, у которого все стороны равны, называется равносторонним или правильным.
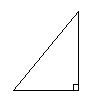 Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется прямоугольным, если у него есть прямой угол, то есть угол в 90°. Сторона прямоугольного треугольника, противолежащая прямому углу, называется гипотенузой, две другие стороны называются катетами.
Треугольник называется остроугольным, если все три его угла — острые, то есть меньше 90°.
Треугольник называется тупоугольным, если один из его углов — тупой, то есть больше 90°.
Замечание: Сумма углов любого треугольника равна 180 градусам!
Основные линии треугольника
Медиана
Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны этого треугольника. 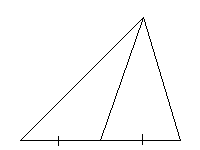
Свойства медиан треугольника
1. Медиана разбивает треугольник на два треугольника одинаковой площади.
2. Медианы треугольника пересекаются в одной точке, которая делит каждую из них в отношении 2:1, считая от вершины. Эта точка называется центром тяжести треугольника.
3. Весь треугольник разделяется своими медианами на шесть равновеликих треугольников.
4. Медиана, опущенная из середины прямого угла равна половине гипотенузы и равна радиусу описанной окружности.
5. В равнобедренном треугольнике медиана, проведенная из вершины, является так же биссектрисой и высотой.
Биссектриса
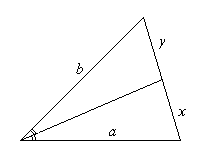 Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Биссектриса угла — это луч, который исходит из его вершины, проходит между его сторонами и делит данный угол пополам. Биссектрисой треугольника называется отрезок биссектрисы угла треугольника, соединяющий вершину с точкой на противолежащей стороне этого треугольника.
Свойства биссектрис треугольника
1. Биссектриса угла — это геометрическое место точек, равноудаленных от сторон этого угла.
2. Биссектриса внутреннего угла треугольника делит противолежащую сторону на отрезки, пропорциональные прилежащим сторонам: 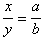 .
.
3. Точка пересечения биссектрис треугольника является центром окружности, вписанной в этот треугольник.
4. Биссектрисы внутреннего и смежного с ним внешнего угла перпендикулярны.
Высота
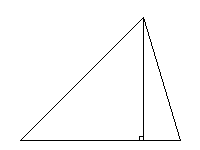 Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Высотой треугольника называется перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону этого треугольника.
Свойства высот треугольника
1. В прямоугольном треугольнике высота, проведенная из вершины прямого угла, разбивает его на два треугольника, подобные исходному.
2. В остроугольном треугольнике две его высоты отсекают от него подобные треугольники.
Срединный перпендикуляр
Прямую, проходящую через середину отрезка перпендикулярно к нему, называют серединным перпендикуляром к отрезку.
Свойства серединных перпендикуляров треугольника 
1. Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Верно и обратное утверждение: каждая точка, равноудаленная от концов отрезка, лежит на серединном перпендикуляре к нему.
2. Точка пересечения серединных перпендикуляров, проведенных к сторонам треугольника, является центром окружности, описанной около этого треугольника.
Средняя линия
 Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.
Средней линией треугольника называется отрезок, соединяющий середины двух его сторон.