Рекомендации для решения задачи №2

Далее ⇒

Рекомендации для решения задачи №1.

Для определения оптимального числа групп необходимо воспользоваться формулой Стерджеса:

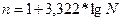, где

n – число групп (целое число);

N – число единиц в статистической совокупности.

Затем следует определить максимальный и минимальный элементы в исследуемой совокупности:

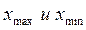
Далее определяется интервал группировки по формуле:

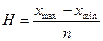где H – интервал группировки.

Строится группировка следующим образом

Средние значения искомых показателей определяются по формуле средней арифметической.

				Таблица 1.1
Зависимость выпуска продукции от среднегодовой стоимости основных фондов
Номер группы	Группы предприятий по стоимости основных фондов	Число предприятий	Выпуск продукции
Всего	В среднем на одно предприятие





Итого

Построить интервальный вариационный ряд и гистограмму распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов и установить характер (тип) этого распределения.

Интервальный вариационный ряд распределения единиц совокупности по признаку Среднегодовая стоимость основных производственных фондов представлен в табл.2

		Таблица 1.2
Интервальный ряд распределения предприятий по стоимости основных производственных фондов
Группа предприятий по стоимости основных фондов	Число предприятий в группе	Накопленная частность группы.%

Задача №2. По данным табл. Приложения 2 выполнить следующие расчеты и представить их в табл. 2.1, 2.2 и табл. 2.3:

2.1. Вычислите цепные и базисные показатели:

а) абсолютные приросты;

б) темпы роста;

в) темпы прироста;

г) абсолютные значения 1% прироста.

Рекомендации для решения задачи №2.

Абсолютный прирост:

Темп роста:

Темп прироста:

Абсолютное значение одного процента прироста:

Средний уровень ряда динамики:

а) для моментных рядов вычисляется по формуле средней хронологической;

б) для интервальных – по формуле средней арифметической.

Средний уровень моментного ряда с равными интервалами рассчитывается по формуле средней хронологической:

Средний абсолютный прирост:

Средний темп роста:

Средний темп прироста:

Прогноз выпуска:

По среднему абсолютному приросту, млн. руб., =

По среднему темпу роста, %, =

						Таблица 2.1
Показатели динамики выпуска продукции
Годы	Выпуск продукции, млн. руб.	Абсолютный прирост, млн. руб.	Темп роста, %	Темп прироста, %	Абсолютное значение 1% прироста
цепной	базисный	цепной	базисный	цепной	базисный
1-й
2-й
3-й
4-й
5-й
6-й

2.2. Вычислите средние показатели динамики.

Таблица 2.2.

Средние показатели ряда динамики:

Средний уровень ряда динамики, млн. руб.,
Средний абсолютный прирост, млн. руб.,
Средний темп роста, %,
Средний темп прироста, %,

2.3. Составить прогноз выпуска на 7-й год:

Таблица 2.3.

Прогноз выпуска на 7-й год:

По среднему абсолютному приросту, млн. руб.,
По среднему темпу роста, %,

Задача №3. По данным таблицы из Приложения 1 рассчитать обобщающие статистические показатели совокупности по изучаемым признакам: среднюю арифметическую ( ), моду (Мо), медиану (Ме), размах вариации (R), дисперсию ( ), средние отклонения – линейное ( ) и квадратическое ( ), коэффициент вариации (Vσ), коэффициент осцилляции (VR ).

Далее ⇒