От момента действующих сил и определение момента инерции маятника и момента сил сопротивления
Описание установки
В лабораторной работе поступательное и вращательное движение тел изучается на установке, основной частью которой является модель маятника Обербека – крестообразный маятник. Схема установки приведена на рис. 2.1.
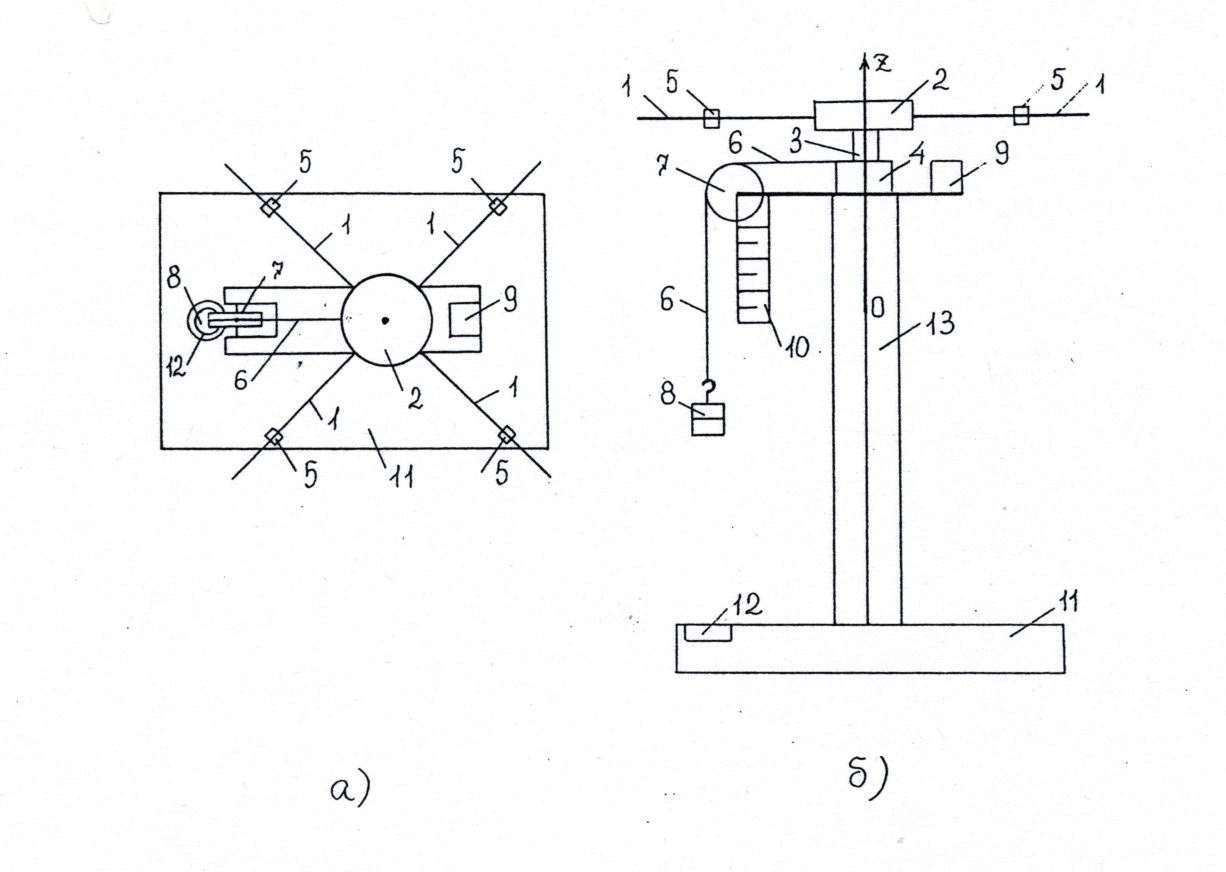
Рис. 2.1
Вращающейся частью установки (рис. 1,а) являются четыре одинаковых стержня 1, укрепленных на цилиндрическом диске 2 под прямым углом друг к другу (крестовина), и два шкива 3 и 4 различного диаметра  , жестко соединенные с диском 2.
, жестко соединенные с диском 2.
На стержнях находятся цилиндрические грузы 5 массой  , которые можно перемещать по стержням и с помощью винтов на них закреплять на выбранных расстояниях
, которые можно перемещать по стержням и с помощью винтов на них закреплять на выбранных расстояниях  на стержнях.
на стержнях.
Диск крестовины и шкивы насажены на общий стержень, закрепленный в подшипниках так, что вся эта система – маятник Обербека – может вращаться вокруг вертикальной оси  , перпендикулярной горизонтальной плоскости крестовины и проходящей через ось диска.
, перпендикулярной горизонтальной плоскости крестовины и проходящей через ось диска.
К шкивам прикрепляется нить 6. Нить перекидывается через блок 7, к свисающему свободному концу нити подвешивается груз 8 массой  .
.
Если, вращая маятник руками, намотать нить на шкив и поднять груз 8 на некоторую высоту  и отпустить маятник, то груз, опускаясь (падая), приводит всю систему в движение. При этом груз совершает поступательное движение, а маятник – вращательное.
и отпустить маятник, то груз, опускаясь (падая), приводит всю систему в движение. При этом груз совершает поступательное движение, а маятник – вращательное.
В установке предусмотрена возможность фиксации груза на выбранной высоте  с помощью электромагнита 9, расположенного в верхней части установки. Высота падения груза
с помощью электромагнита 9, расположенного в верхней части установки. Высота падения груза  измеряется по линейке 10, установленной в верхней части установки, на которой указано расстояние груза от столика установки 11.
измеряется по линейке 10, установленной в верхней части установки, на которой указано расстояние груза от столика установки 11.
Для измерения времени падения груза  используется цифровой секундомер. При нажатии кнопки секундомера «пуск» электромагнит автоматически отключается, и груз начинает опускаться, а секундомер начинает считать время. В место падения груза на столик 11 вмонтирован датчик 12, выключающий секундомер при ударе груза об это место столика установки.
используется цифровой секундомер. При нажатии кнопки секундомера «пуск» электромагнит автоматически отключается, и груз начинает опускаться, а секундомер начинает считать время. В место падения груза на столик 11 вмонтирован датчик 12, выключающий секундомер при ударе груза об это место столика установки.
Подвешивая грузы с разной массой и к разным шкивам, можно изменить момент сил, действующих на маятник, а передвигая цилиндрические грузы на стержнях, можно изменять момент инерции маятника.
Таким образом, установка позволяет измерить высоту падения (опускания) груза  и время падения
и время падения  , на основе которых при заданных значениях массы груза
, на основе которых при заданных значениях массы груза  и диаметра шкива
и диаметра шкива  можно определить кинематические, динамические и энергетические характеристики поступательного движения груза и вращательного движения маятника, принимая их равноускоренными.
можно определить кинематические, динамические и энергетические характеристики поступательного движения груза и вращательного движения маятника, принимая их равноускоренными.
Установка позволяет также проверить основной закон динамики вращательного движения
 (2.1)
(2.1)
т.е. прямо-пропорциональную зависимость углового ускорения маятника от момента сил  , действующих на тело:
, действующих на тело:
a ~ M (2.2)
при постоянном моменте инерции тела  , и обратно-пропорциональную зависимость углового ускорения
, и обратно-пропорциональную зависимость углового ускорения  от момента инерции
от момента инерции  тела:
тела:
 (2.3)
(2.3)
при постоянном моменте действующих сил  .
.
Задание1. Проверка зависимости углового ускорения
от момента действующих сил и определение момента инерции маятника и момента сил сопротивления
Теория метода
Проверка зависимости углового ускорения от момента действующих сил. На маятник действуют сила натяжения нити  и сила сопротивления
и сила сопротивления  , обусловленная трением в подшипниках и сопротивлением воздуха. (Сила тяжести маятника уравновешена силой реакции стойки 13, на которую укреплен маятник).
, обусловленная трением в подшипниках и сопротивлением воздуха. (Сила тяжести маятника уравновешена силой реакции стойки 13, на которую укреплен маятник).
Моменты сил  и
и  обозначим через
обозначим через  и
и  .
.
С учетом знаков моментов сил  и
и  согласно основному закону динамики вращательного движения тел (2.1)
согласно основному закону динамики вращательного движения тел (2.1)
 (2.4)
(2.4)
Момент инерции  маятника при неизменном расположении цилиндрических грузов 5 на стержнях и момент сил сопротивления
маятника при неизменном расположении цилиндрических грузов 5 на стержнях и момент сил сопротивления  , если пренебречь зависимостью силы сопротивления от скорости, постоянны. Поэтому проверка зависимости (2.2) сводится к проверке линейной зависимости углового ускорения
, если пренебречь зависимостью силы сопротивления от скорости, постоянны. Поэтому проверка зависимости (2.2) сводится к проверке линейной зависимости углового ускорения  от момента силы натяжения нити
от момента силы натяжения нити  (2.4).
(2.4).
Момент силы натяжения  можно изменять, подвешивая к свободному концу нити грузы 8 с разной массой
можно изменять, подвешивая к свободному концу нити грузы 8 с разной массой  и наматывая нить на разные шкивы.
и наматывая нить на разные шкивы.
Экспериментально определенные значения высоты падения груза  , времени падения
, времени падения  и заданные значения масс грузов
и заданные значения масс грузов  и диаметров шкивов
и диаметров шкивов  позволяют определить угловое ускорение маятника
позволяют определить угловое ускорение маятника  (см. п.п. 1.3,г в «Заданиях …») и момент силы натяжения
(см. п.п. 1.3,г в «Заданиях …») и момент силы натяжения  (см. п.п. 1.6 в «Заданиях …») при различных
(см. п.п. 1.6 в «Заданиях …») при различных  и
и  , и, построив график зависимости
, и, построив график зависимости  от
от  , убедиться в справедливости зависимости (2.4).
, убедиться в справедливости зависимости (2.4).
Определение момента инерции маятника J и момента сил сопротивления  . График зависимости углового ускорения от момента силы натяжения
. График зависимости углового ускорения от момента силы натяжения  позволяет определить момент инерции маятника J и момент сил сопротивления
позволяет определить момент инерции маятника J и момент сил сопротивления 
Сопоставив уравнение (2.4) с уравнением прямой в виде

заключаем, что угловой коэффициент  , равный тангенсу угла наклона прямой α(M), в нашем случае равен:
, равный тангенсу угла наклона прямой α(M), в нашем случае равен:

Отсюда 
Используя определение тангенса угла, получим:
 (2.5)
(2.5)
где Δ  – выбранный интервал момента силы натяжения,
– выбранный интервал момента силы натяжения,  - соответствующий Δ
- соответствующий Δ  интервал углового ускорения, определенный по графику зависимости
интервал углового ускорения, определенный по графику зависимости  от
от  .
.
Отрезок  , отсекаемый прямой на оси
, отсекаемый прямой на оси  , является моментом силы натяжения, при котором α = 0, т.е. моментом силы натяжения, при котором маятник начинает вращаться. Поэтому согласно уравнению (2.4)
, является моментом силы натяжения, при котором α = 0, т.е. моментом силы натяжения, при котором маятник начинает вращаться. Поэтому согласно уравнению (2.4)
 (2.6)
(2.6)
(Из (2.4) следует, что при 

 маятник должен вращаться с угловым
маятник должен вращаться с угловым
ускорением  т.е. в обратную сторону, но этого не будет, т.к.
т.е. в обратную сторону, но этого не будет, т.к.
сила сопротивления  и
и  возникают только при действии
возникают только при действии  , причем при
, причем при 

 момент сил сопротивления
момент сил сопротивления  =
=  ).
).
Таким образом, график зависимости α от  позволяет определить момент инерции маятника J при выбранном расстоянии грузов 5 до оси вращения (2.5) и момент сил сопротивления
позволяет определить момент инерции маятника J при выбранном расстоянии грузов 5 до оси вращения (2.5) и момент сил сопротивления  (2.6).
(2.6).