МЕХАНИЧЕСКИЕ СОСТОЯНИЯ ДЕФОРМИРУЕМЫХ ТЕЛ

Задачи экспериментального изучения механических свойств материалов

Основные задачи экспериментальных изучений механических характеристик материалов следующие:

1) Определение механических характеристик материала при теоретических исследованиях с целью их проверки и установления закономерностей.

2) Определение основных механических характеристик материала с целью оценки его конструктивных качеств.

3) Определение необходимых механических характеристик материала с целью оценки его технологического поведения при различных способах обработки.

4) Определение некоторых механических характеристик материала с целью оценки его однородности и стандартности при изготовлении.

5) Определение необходимых механических характеристик материала при создании новых строительных материалов.

Правильное конструирование и эффективное использование строительных конструкций и материалов не возможно без тщательного изучения механических свойств материалов. Необходимые для тех или иных целей механические характеристики определяются путем лабораторных испытаний.

2.2 Факторы определяющие характеристики материалов

Механические характеристики материалов определяются по следующими факторами:

  • веществом, его структурой и свойствами;
  • конструктивными особенностями элемента, т. е, размерами, формой, наличием концетраторов напряжений, состоянием поверхности обработки;
  • условиями при нагружении: температурой, скоростью, повторяемостью нагрузки и др.

Поведение материалов характеризуется существенным изменением формы и размеров, при этом к моменту разрушения развиваются значительные деформации, не исчезающие после снятия нагрузки такие материалы называют пластичными. Следовательно, под пластичностью понимают свойство твердых тел сохранять остаточные деформации.

При хрупком поведении разрушение наступает при весьма малых деформациях, и материалы с такими свойствами называют хрупкими.

Основные макромеханические характеристики пластичных и хрупких материалов — упругость, пластичность, вязкость и др. показывают относительное состояние материала.

МЕХАНИЧЕСКИЕ СОСТОЯНИЯ ДЕФОРМИРУЕМЫХ ТЕЛ

В упругом состоянии деформации обратимы, и вся энергия, затраченная на деформирование, при разгрузке возвращается .Для любого твердого тела процесс деформирования начинается с упругой деформации. Изотропное тело имеет две константы упругости:

- модуль упругостиЕ

- коэффициент Пуассонаµ

Для анизотропных тел число упругих констант в общем случае равно 21. Из основных констант упругости можно получить их производные—модуль сдвига G, модуль объемной деформации К и постоянную Ламе λ.

Вязкое сопротивление — в некотором смысле противоположно упругому — работа внешних сил, уравновешенных силами вязкого сопротивления, полностью рассеивается в виде тепла. Вязкое сопротивление определяется величиной касательной силы, необходимой для поддержания ламинарного скольжения слоев, или течения с определенной скоростью. Вязкость можно определить как сопротивление течению.

Представление о вязкоупругой деформации дает поведение моделей: -упругая деформация, подчиняющаяся закону Гука;

-вязкая деформация, подчиняющаяся закону Ньютона.

Наиболее распространенными в теории линейной вязко-упругости являются реологические модели Максвелла и Фойгта, дающие связь между напряжениями и деформациями и скоростями их изменения:

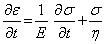— модель Максвелла,

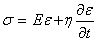— модель Фойгта,

тде — коэффициент вязкости.

Пластическое состояние—характеризуется наличием остаточных деформаций, фиксируемых после снятия внешних нагрузок. Объем тела при пластической деформации не изменяется; условие постоянства объема записывается в виде θ=Ɛх+Ɛу+Ɛz=0(эксперименты показывают, что изменение объема не превышает 0,5%).

В случае, когда все напряжения изменяются пропорционально одной из составляющих, в процессе пластической деформации направления главных деформаций совпадают с направлениями главных нормальных напряжений, направления максимальных сдвигов — с направлениями максимальных касательных напряжений. Одной из распространенных моделей поведения материала при упруго-пластических деформациях является модель пластичности, основанная на деформационной теории Генки—Ильюшина, описываемая уравнениями:

Здесь — средняя деформация,

— среднее напряжение,

Ψ— безразмерный коэффициент, называемый параметром пластичности (с точностью до множителя он совпадает с интенсивностью касательных напряжений). При Ψ=1 эта модель описывает поведение упругого материала.

Состояние разрушения — состояние, при котором за счет интенсивного развития трещин в материале тела начинается нарушение его сплошности и непрерывности. Физический процесс разрушения материала представляется в виде двух основных стадий — стадии рассеянных разрушений (зарождение и развитие микроскопических трещин) и стадии развития магистральной трещины. Очаги зарождения микротрещин распределены по всему объему материала, находящегося в однородном напряженном состоянии, достаточно равномерно. Относительная длительность первой и второй стадии разрушения зависит от свойств материала, характера напряженного состояния и условий нагружения.