ПРИМЕР ОПРЕДЕЛЕНИЯ ГЕОМЕТРИЧЕСКИХ ХАРАКТЕРИСТИК СЛОЖНОГО ПОПЕРЕЧНОГО СЕЧЕНИЯ

Исходные данные:

Двутавр №16 (ГОСТ 8239-72)

Равнобокий уголок 80 x 80x 6 (ГОСТ 9509-72)

Прямоугольник 200 x 20

РЕШЕНИЕ

1)Расположим составное сечение (рис.6) в первой четверти координатной плоскости 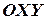(чтобы в дальнейшем не ошибиться со знаками вычисляемых геометрических характеристик).

2) Пронумеруем фигуры:

прямоугольник - (фигура 1), двутавр - (фигура 2), равнобокий уголок - (фигура 3).

Проведем для каждой фигуры собственные центральные оси ( рис.6, рис.11).

Для прямоугольника и двутавра эти оси будут и главными осями, так как у каждой из этих фигур есть оси симметрии.

Для каждой фигуры найдем все необходимые геометрические характеристики и координаты центра тяжести относительно первоначальных осей .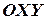

а) Прямоугольник (фигура1)

=200мм=20см,

=20мм=2см,

, (т.к. оси являются главными центральными).

б) Двутавр № 16 (фигура 2)

(т.к. оси являются главными центральными).

Замечание: при выборе для двутавра и швеллера необходимо учитывать, что их табличное расположение может отличаться от рассматриваемого. В частности если имеем:

а) вертикальное расположение швеллера(двутавра), то:

б) горизонтальное расположение швеллера (двутавра),то:

в)Равнобокий уголок 80x80x6 (фигура 3)

(т.к. оси являются главными центральными для равнобокого уголка).

Определим центробежный момент . Для этого воспользуемся первым (или вторым) соотношением из (14). Знак угла определяется направлением поворота от центральной оси к главной.

, если поворот от оси к оси происходит по часовой стрелке;

, если поворот от оси к оси происходит против часовой стрелки;

Подставляя в первое соотношение из (14), получим:

Таким образом, центробежный момент относительно центральных осей равен .

Замечание:знак центробежного момента относительно осей (см.рис.10) определяется в зависимости от расположения уголка относительно этих осей.

Для уголка в нашем примере (см на рис.10а)), большая часть сечения (заштрихованная) расположена в 1-oй четверти где и в 3-ей четверти, где .

Таким образом, по определению ( ) для всего сечения центробежный момент .

г) Определим координаты центров тяжести , у каждой фигуры относительно первоначальных осей :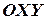

3) Вычислим координаты центра тяжести всей фигуры относительно первоначальных осей 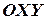, т.е. координаты :

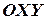По координатам находим точку относительно и через нее проводим центральные оси , параллельно первоначальным осям (рис.11).

4) Вычислим моменты инерции каждой простой фигуры относительно первоначальных осей 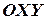по формулам параллельного переноса (10) и просуммируем моменты инерции согласно (11).Таким образом:

Таким образом,

Так,

Просуммируем,

5) Вычислим моменты инерции всего сечения относительно центральных осей и по формулам (12):

6) Определим положение главных центральных осей сечения . Главная центральная ось сечения расположена под углом к центральной оси согласно (13):

(17)

Таким образом, главные центральные оси повернуты относительно центральных осей на угол (см. рис.11) против хода часовой стрелки (так как угол положителен).

7) Вычислить главные моменты инерции сложного сечения по (14):

(18)

Проверка арифметических вычислений в (17) и (18).

а) Из последнего соотношения (14):

б) Согласно соотношениям (16):

Таким образом, имеет место равенство:

Итак,

8). Определим моменты инерции относительно центральных осей , расположенных под углом ( ) к главным центральным осям .

Согласно соотношениям (15):

9)Произведем проверку последних вычислений:

10)Вычислим радиусы инерции сечения относительно главных осей.

- откладываем на оси от точки

На этих осях строим эллипс инерции (рис.11)

Заключение

1) Положение главных центральных осей , показано на рис.11. Главные моменты инерции сечения равны

2) Положение эллипса инерции сечения говорит о том, что при изгибе балки в направлении оси ее жесткость и прочность будут наибольшими, а при изгибе в направлении оси - наименьшими.

Примечание

Данная задача может быть легко алгоритмизирована и записана в виде программы для ЭВМ. Этот пример был проcчитан с помощью пакета Mathematica 5 (см. Приложение 2

КОНТРОЛЬНЫЕ ВОПРОСЫ ПО ТЕМЕ