Необхідна умова диференційовності функції у точці

Основні поняття

Означення. Якщо кожній точці 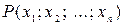множини D
n-вимірного простору поставлено у відповідність за деяким
законом одне і тільки одне дійсне число 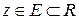, то кажуть, що в області задано функцію n незалежних змінних . При цьому D називають областю визначення функції, Е — областю значень функції.

Зокрема, при n = 2 говорять, що задана функція двох змінних , якщо кожній парі на площині поставлено у відповідність тільки одне число z. Для прикладних питань економіки має значення розгляд функції двох або трьох незалежних змінних.

Приклад. Витратами на виробництво даного виробу при даній техніці виробництва є функція матеріальних витрат x і витрат на оплату робочої сили y: . Це є функція витрат виробництва.

Як і функцію однієї змінної, функції двох змінних можна зобразити:

— аналітично (у вигляді формули), наприклад: ,

— таблично (у вигляді таблиці).

— графічно.

Для графічного зображення функції двох змінних використовуємо систему координат Оxyz у тривимірному просторі (рис. 1).

Рис. 1

Кожній парі чисел x та y відповідає точка площини Оxy. У точці проводимо пряму, перпендикулярну до площини Оxy, та позначаємо на ній відповідне значення функції z; дістаємо в просторі точку Q з координатами . Точки Q, які відповідають різним значенням незалежних змінних, утворюють певну поверхню у просторі. Така поверхня є графічним зображенням функції .

Існує й інший спосіб геометричного зображення функції двох змінних — зображення за допомогою ліній рівня.

Означення. Лінією рівня називається множина всіх точок площини, в яких функція набуває однакових значень. Рівняння ліній рівня записують у вигляді .

Частинні похідні функції двох змінних

Нехай функція визначена в деякому околі точки . Надамо незалежним змінним x та y приросту відповідно та так, щоб точка не виходила за межі вказаного околу. Тоді й точки , також належатимуть розглядуваному околу (рис. 2).

Рис. 2

Означення. Різницю називають повним приростом функції і позначають . Різницю називають частинним приростом за х, а різницю — частинним приростом за y функції .

, .

Означення. Нехай функція визначена в точці і в її деякому околі. Якщо існує границя , то вона називається частинною похідною за х (за у) функції у точці і позначається , або , або . Таким чином, , . Із означення частинних похідних матимемо, що вони шукаються за тими правилами, що й похідні функції однієї змінної. Треба лише пам’ятати, що при знаходженні у вважається сталою, а при знаходженні змінна х вважається сталою.