Способы задания движения точки

Моменты сил относительно точки и оси

Момент силы относительно точки

– вектор, численно равный произведению модуля силы на плечо и направленный перпендикулярно плоскости, содержащей силу и точку, в такую сторону, чтобы смотря ему навстречу, видеть силу стремящейся повернуться против хода час.стрелки. Плечо "h"– кратчайшее расстояние от точки до линии действия силы.

Момент силы равен векторному произведению вектора R на 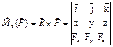вектор F. Модуль векторного произведения: 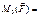R×F×sina= F×h. Для плоской сист. сил обычно находят не вектор момента, а только его модуль: ±F×h, >0 – против час.стр.; <0 – по час.стр. Свойства момента силы: 1) момент силы не изменяется при переносе точки приложения силы вдоль ее линии действия; 2) момент силы относит. точки =0 только тогда, когда сила =0 или когда линия действия силы проходит через точку (т.е. плечо =0). Если x,y,z – координаты точки приложения силы, F_x, F_y, F_z – проекции силы на оси координат и точка 0 – начало координат, то

=(yF_z – zF_y)i +(zF_x – xF_z)j+(xF_y – yF_x)k, откуда проекции момента силы на оси коорд.: М₀_x(F)=yF_z – zF_y; М₀_y(F)=zF_x – xF_z; М₀_z(F)=xF_y – yF_x_.

Момент силы отн-но оси.

Моментом силы отн-но оси наз-ся алгебраический момент проекции силы на пл-ть, ^ оси относительно точки пересечения оси с пл-тью.

М_z(F)=±F^’ h=±2S_D_OA’B’

Момент силы относительно оси =0, если сила ½½ оси или линия действия силы пересекает ось. Момент силы относительно оси =0, если сила и ось в одной плоскости.

М_z(F)=½М₀( F)½cosa

Момент силы отн-но оси – это есть проекция вектора момента силы отн-но любой точки оси на эту ось.

S_D_OA’B’ =S_DOAB cosa.

Способы задания движения точки.

Задать движение точки означает задать ее положение в каждый момент времени. Положение это должно определяться, как уже отмечалось, в какой-либо системе координат. Однако для этого не обязательно всегда задавать сами координаты; можно использовать величины, так или иначе с ними связанные. Ниже описаны три основных способа задания движения точки.

1.Естественный способ. Этим способом пользуются, если известна траектория движения точки. Траекторией называется совокупность точек пространства, через которые проходит движущаяся материальная частица. Это линия, которую она вычерчивает в пространстве. При естественном способе необходимо задать :

а) траекторию движения (относительно какой-либо системы координат);

б) произвольную точку на ней нуль, от которого отсчитывают расстояние S до движущейся частицы вдоль траектории;

в) положительное направление отсчета S (при смещении точки М в противоположном направлении S отрицательно);

г) начало отсчета времени t;

д) функцию S(t), которая называется законом движения точки.

2. Координатный способ. Это наиболее универсальный и исчерпывающий способ описания движения. Он предполагает задание:

а) системы координат (не обязательно декартовой) q1, q2, q3;

б) начало отсчета времени t;

в) закона движения точки, т.е. функций q1(t), q2(t), q3(t).

Говоря о координатах точки, мы всегда будем иметь в виду (если не оговорено противное) ее декартовы координаты.

3. Векторный способ. Положение точки в пространстве может быть определено также и радиус-вектором, проведенным из некоторого начала в данную точку. В этом случае для описания движения необходимо задать:

а) начало отсчета радиус-вектора r;

б) начало отсчета времени t;

в) закон движения точки r(t).

Поскольку задание одной векторной величины r эквивалентно заданию трех ее проекций x, y, z на оси координат, от векторного способа легко перейти к координатному. Если ввести единичные векторы i, j, k ( i = j = k = 1), направленные соответственно вдоль осей x, y и z (рис. 2), то, очевидно, закон движения может быть представлен в виде*)

r(t) = x(t)i +y(t)j+z(t)k.

Преимущество векторной формы записи перед координатной в компактности (вместо трех величин оперируют с одной) и часто в большей наглядности.

Способы задания движения точки.

s=f(t) –естественный способ задания движения, прямолинейное движение: х=f(t).

Координатный способ: x=f1(t), y=f2(t), z=f3(t). Уравнение траектории: f(x,y,z)=0.

Векторный способ: радиус-вектор = ,

модуль , направляющие косинусы: и т.д

6. Определение скорости точки при различных способах задания ее движенияВектор_скорости: ; .Проекции_скорости: , , . Модуль_скорости: , направляющие_косинусы: и т.д.

Естественный_способ: , , – орт касательной.

Движение в полярной системе координат: r=r(t) – полярный радиус, j=j(t) – угол. Проекции скорости на

радиальное направление , поперечное направление ,

модуль скорости .; x=rcosj, y=rsinj.

Определение ускорения точки при различных способах задания ее движения

Ускорение_точки. .

Проекции_уск.-я: и т.д.

Модуль_уск.-я: ,направляющ.косинусы:

, и т.д.

Проекции уск. на радиальное напр-ние ,

поперечное_напр-ние , модуль_уск-я . . 7. Скорости и ускорения различных точек вращающегося тела.

Вращательным движением называется движение, при котором все точки тела описывают окружности. Центры этих окружностей лежат на прямой, называемой осью вращения. В общем случае движение твердого тела можно представить как результат сложения поступательного и вращательного движений. При вращательном движении все точки тела описывают окружности, при этом радиус-векторы поворачиваются на угол за время . Для того, чтобы указать, в какую сторону совершается поворот, элементарные повороты изображают в виде вектора . По модулю равен величине угла поворота, а направление подчиняется правилу правого винта (рис. 1.6). Быстроту вращения характеризует угловая скорость .

Рис.1.6Угловой скоростью называется производная от угла поворота по времени.
Модуль угловой скорости равен .Вектор угловой скорости направлен вдоль оси вращения по правилу правого винта (рис. 1.6). При равномерном вращении угловая скорость связана с периодом обращения Т и частотой вращения следующим образом

Модуль угловой скорости выражается в радианах в секунду (рад/с). Быстрота изменения угловой скорости характеризуется угловым ускорением .

Угловым ускорением называется производная от угловой скорости по времени. Модуль углового ускорения равен При вращении тела вокруг неподвижной оси угловое ускорение также как и угловая скорость направлено вдоль оси вращения. При ускоренном движении эти вектора сонаправлены , при замедленном - противоположны Угловое ускорение измеряется в рад/с². При равномерном вращении

При равнопеременном вращении

где - начальная угловая скорость.
Знак"+" - при равноускоренном движении.
Знак "-" - при равнозамедленном движении.

8. Плоскопараллельное движение твердого тела

Движение, при котором каждая точка тела движется в плоскости параллельно некоторой неподвижной плоскости.

Плоское движение является сложным. Его всегда можно рассмотреть как совокупность поступательного и вращательного.

Далее ⇒