Раздел 3. МОДЕЛИ КРАВООБРАЩЕНИЯ

СОДЕРЖАНИЕ И СТРУКТУРА ТЕСТОВЫХ МАТЕРИАЛОВ

Тематическая структура

СОДЕРЖАНИЕ ТЕСТОВЫХ МАТЕРИАЛОВ Раздел 1. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА Раздел	Подраздел	Тема
Раздел 1. МЕХАНИЧЕСКИЕ СВОЙСТВА ТВЕРДЫХ ТЕЛ	КРИСТАЛЛИЧЕСКИЕ И АМОРФНЫЕ ТЕЛА
	БАРОМЕТРИЧЕСКАЯ ФОРМУЛА
	ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ
	МЕХАНИЧЕСКИЕ ВОЛНЫ
Раздел 2.ТЕРМОДИНАМИКА	ЭФФЕКТ ДОПЛЕРА
	ИДЕАЛЬНЫЙ ГАЗ
Раздел 3. МОДЕЛИ КРАВООБРАЩЕНИЯ
Раздел 4. МЕХАНИКА
Раздел 5. ЭЛЕКТРИЧЕСТВО
Раздел 6. МОЛЕКУЛЯРНАЯ ФИЗИКА
Раздел 7. ЗАДАЧИ

Задание {{ 1 }} ТЗ 1 Тема 1-1-0

Особенностью аморфных тел является их:

+ изотропность

£ анизотропность

£ упорядоченность структуры

£ упругость

£ пластичность

Задание {{ 2 }} ТЗ 2 Тема 1-1-0

Примером аморфного тела является:

£ турмалин

£ поваренная соль

£ исландский шпат

+ стекло

£ медь

Задание {{ 3 }} ТЗ 3 Тема 1-1-0

Особенностью кристаллических тел является:

£ упругость

£ изотропность

+ упорядоченность структуры

£ пластичность

£ ближний порядок

Задание {{ 4 }} ТЗ 4 Тема 1-1-0

Примером кристаллического тела является:

£ стекло

+ поваренная соль

£ янтарь

£ пластмасса

£ эбонит

Задание {{ 5 }} ТЗ 5 Тема 1-1-0

Явление полиморфизма вещества состоит в том, что оно:

£ может обладать как изотропностью, так и анизотропией

£ может находиться при некоторой температуре одновременно в нескольких агрегатных состояниях

+ может существовать в нескольких кристаллических модификациях, отличающихся физическими свойствами

£ может существовать в нескольких агрегатных состояниях, отличающихся температурами

£ может обладать структурами, характеризующимися как дальним, так и ближним порядком

Задание {{ 6 }} ТЗ 6 Тема 1-1-0

Полиморфным переходом называется переход:

£ из одного агрегатного состояния в другое

£ из изотропного состояния в анизотропное

£ из кристаллического состояния в аморфное

£ из аморфного состояния в кристаллическое

+ из одной кристаллической модификации в другую

Задание {{ 7 }} ТЗ 7 Тема 1-1-0

Структуры кристаллических решеток экспериментально изучаются с помощью:

+ дифракции рентгеновского излучения

£ интерферометра

£ поляриметра

£ люминесцентного микроскопа

£ фотоэлектроколориметра

Задание {{ 8 }} ТЗ 8 Тема 1-1-0

В объемноцентрированной кубической решетке частицы располагаются:

£ только в вершинах куба

+ в вершинах куба и в его центре

£ только в центре куба

£ в вершинах куба и в центрах граней

£ только в центрах граней

Задание {{ 9 }} ТЗ 9 Тема 1-1-0

В гранецентрированной кубической решетке частицы располагаются:

£ в вершинах куба и в его центре

£ только в вершинах куба

+ в вершинах куба и в центрах граней

£ только в центре куба

£ только в центрах граней

Задание {{ 10 }} ТЗ 10 Тема 1-1-0

В твердых телах частицы (молекулы, атомы, ионы):

£ вращаются вокруг собственной оси

+ совершают тепловые колебания около положений равновесия

£ движутся поступательно внутри твердого тела

£ одновременно участвуют в поступательном и вращательном движении

£ неподвижны

Задание {{ 15 }} ТЗ 15 Тема 1-1-0

Упругими называются деформации, которые:

£ при снятии напряжения остаются постоянными

£ не зависят от приложенного напряжения

+ при снятии напряжения практически полностью исчезают

£ прямо пропорциональны приложенной силе

£ обратно пропорциональны приложенной силе

Задание {{ 16 }} ТЗ 16 Тема 1-1-0

Пластическими называются деформации, при которых:

+ тело уже не восстанавливает свои первоначальные размеры и сохраняется остаточная деформация

£ форма и размеры тела не зависят от приложенного напряжения

£ напряжения при снятии деформирующей силы практически полностью исчезают

£ напряжения прямо пропорциональны приложенной силе

£ напряжения обратно пропорциональны приложенной силе

Задание {{ 19 }} ТЗ 19 Тема 1-2-0

Костная ткань в основном состоит из:

£ окиси кальция

£ коллагена

£ гидроксилопатита

+ гидроксилопатита и коллагена

£ фибрилл

Задание {{ 37 }} ТЗ 11 Тема 1-1-0

Отметьте правильный ответ

Относительным удлинениемилиотносительной деформацией ε называется:

+ отношение абсолютного удлинения Δl к первоначальной длине l образца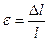

£ Отношение первоначальной длины l к абсолютному удлинению Δl образца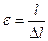

£ Произведение абсолютного удлинения Δl на первоначальную длину l образца

£ Величина

Задание {{ 38 }} ТЗ 12 тема 1-1-0

Механическим напряжением называется:

£ Отношение площади S сечения тела к модулю внешней силы F:

£ Отношение абсолютного удлинения Δl к первоначальной длине l образца

+ Отношение модуля внешней силы F к площади S сечения тела

£ Отношение первоначальной длины l к абсолютному удлинению Δl образца

£ Величина

Задание {{ 39 }} ТЗ 13 Тема 1-1-0

Диаграммой растяжения называется графическое изображение зависимости между:

£ Δl и l

£ Δl и F

£ ε и F

£ σ и F

+ ε и σ

Задание {{ 40 }} ТЗ 14 Тема 1-1-0

Обозначая через Е модуль Юнга, закон Гука можно записать как:

Задание {{ 42 }} ТЗ 17 Тема 1-1-0

Обозначая через G модуль сдвига, относительную деформацию сдвига можно записать в виде:

Задание {{ 43 }} ТЗ 18 Тема 1-1-0

Обозначая через В модуль всестороннего сжатия, а через p - давление сжатия, относительную деформацию сжатия можно записать в виде:

БАРОМЕТРИЧЕСКАЯ ФОРМУЛА

Задание {{ 20 }} ТЗ 20 Тема 1-2-0

Атмосфера Земли обязана своим существованием наличию:

+ только силы притяжения к Земле

£ только теплового движения молекул воздуха

£ только вязкости воздуха

£ одновременно силы притяжения к Земле и теплового движения молекул

£ одновременно силы притяжения к Земле и вязкости воздуха

Задание {{ 21 }} ТЗ 21 Тема 1-2-0

С высотой над поверхностью Земли давление атмосферы:

£ возрастает по квадратичному закону

£ убывает по линейному закону

£ возрастает по линейному закону

+ убывает по экспоненциальному закону

£ остается постоянным

Задание {{ 23 }} ТЗ 23 Тема 1-2-0

Приведите в соответствие символы в барометрической формуле и величины, которые они обозначают:

P	давление на некоторой высоте
Pо	давление у поверхности Земли
R	универсальная газовая постоянная
h	высота над поверхностью Земли
T	температура
g	ускорение свободного падения

Задание {{ 24 }} ТЗ 24 Тема 1-2-0

Барометрической формулой пользуются для определения:

£ температуры воздуха на некоторой высоте путем измерения давления

£ давления воздуха путем измерения его температуры

£ давления воздуха через молярную массу воздуха

£ температуры воздуха у поверхности Земли путем измерения давления

+ высоты над Землей путем измерения давления

Задание {{ 25 }} ТЗ 25 Тема 1-2-0

Барометрическая формула была получена с помощью:

+ первого закона термодинамики

£ основного уравнения кинетической теории газов

£ уравнения состояния идеального газа

£ закона Бойля-Мариотта

£ объединенного газового закона

Задание {{ 26 }} ТЗ 26 Тема 1-2-0

Барометрическая формула была получена в предположении:

£ постоянства давления на всех высотах

+ постоянства температуры на всех высотах

£ отсутствия взаимодействия между молекулами воздуха

£ наличия только кулоновского взаимодействия между молекулами воздуха

£ постоянства ускорения свободного падения на всех высотах

Задание {{ 46 }} ТЗ 27 Тема 1-3-0

Закон убывания плотности воздуха с высотой описывается выражением:

Задание {{ 260 }} ТЗ 22 Тема 1-2-0

С высотой над поверхностью Земли давление атмосферы математически описывается выражением:

ГАРМОНИЧЕСКИЕ КОЛЕБАНИЯ

Задание {{ 28 }} ТЗ 28 Тема 1-3-0

Гармоническими называются колебания:

£ которые возникают в системе при участии внешней силы

£ при которых их амплитуда под действием силы трения постепенно уменьшается

+ при которых колеблющаяся величина изменяется в зависимости от времени по закону синуса или косинуса

£ при которых механические возмущения распространяются в пространстве и переносят энергию

£ при которых их скорость остается постоянной

Задание {{ 29 }} ТЗ 29 Тема 1-3-0

Примером гармонических колебаний могут служить:

+ колебания математического маятника

£ колебания физического маятника

£ периодические подскакивания в реальных условиях мяча, упавшего на землю

£ круги, расходящиеся на поверхности воды от брошенного камня

£ колебания температуры окружающей среды

Задание {{ 33 }} ТЗ 33 Тема 1-2-0

Фаза колебаний представляет собой:

£ величину, численно равную времени, в течение которого совершается одно полное колебание

£ величину, численно равную наибольшему отклонению колеблющегося тела от положения равновесия

£ величину, численно равную числу колебаний за единицу времени

+ величину, характеризующую положение колеблющейся точки в данный момент времени

£ величину скорости распространения колебаний в данный момент времени

Задание {{ 34 }} ТЗ 34 Тема 1-3-0

Уравнение гармонических колебаний было получено в предположении:

+ малости отклонения маятника от положения равновесия

£ наличия вынуждающей силы, действующей на маятник

£ отсутствия начальной фазы колебания

£ равенства нулю кинетической энергии маятника в положении равновесия

£ наличия силы трения в точке подвеса маятника

Задание {{ 48 }} ТЗ 31 Тема 1-3-0

В выражении для смещения материальной точки X = А₀sin(ω₀t + ...) в случае гармонических колебаний пропущен символ:

Задание {{ 49 }} ТЗ 32 Тема 1-3-0

В выражении для смещения материальной точки X = А₀sin(ω₀t + φ₀ ) в случае гармонических колебаний символ φ₀ означает:

£ частоту колебаний

+ начальную фазу колебаний

£ период колебаний

£ амплитуду колебаний

£ скорость распространения колебаний

Задание {{ 50 }} ТЗ 35 Тема 1-3-0

Энергия гармонических колебаний описывается выражением:

Задание {{ 51 }} ТЗ 37 Тема 1-3-0

Приведите в соответствие колебательные системы и периоды их колебаний:

Математический маятник
Груз на пружине
Колебательный контур
Физический маятник

Задание {{ 250 }} ТЗ 30 Тема 1-3-0

Гармонические колебания описываются уравнением:

Задание {{ 251 }} ТЗ 219 Тема 1-5-0

Не может служить примером гармонических колебаний:

£ колебания математического маятника

+ электромагнитные колебания в колебательном контуре

£ затухающие колебания

£ колебания физического маятника

£ колебания груза на пружине

Задание {{ 249 }} ТЗ 36 Тема 1-3-0

Скорость колебательного процесса может быть найдена путем:

+ Нахождения произвольной смещения маятника по времени

£ Интегрирования уравнения колебаний

£ Деления амплитуды колебаний на их период

Задание {{ 252 }} ТЗ 220 Тема 1-5-0

Неверным является утверждение о том, что:

£ амплитуда гармонических колебаний не зависит от их частоты

£ амплитуда гармонических колебаний не зависит от их периода

+ частота колебаний не зависит от их периода

£ смещение колеблющейся точки зависит от фазы колебаний

£ смещение колеблющейся точки зависит от времени

Задание {{ 253 }} ТЗ 221 Тема 1-5-0

Не подчиняется гармоническому закону следующее математическое выражение:

Задание {{ 254 }} ТЗ 222 Тема 1-5-0

Неверным является утверждение о том, что гармонические колебания:

+ совершаются по закону синуса

£ совершаются по закону косинуса

£ могут иллюстрироваться периодическими изменениями температуры

£ это явления, при которых система, будучи выведена из состояния равновесия, возвращается в него через равные промежутки времени

£ совершаются только при условии отсутствия затухания

Задание {{ 255 }} ТЗ 223 Тема 1-5-0

Скорость гармонических колебаний не может быть найдена:

£ из уравнения гармонических колебаний

+ путем применения операции дифференцирования

£ путем нахождения производной по времени от уравнения колебаний

£ делением амплитуды колебаний на их частоту

£ путем интегрирования выражения для ускорения колебаний

Задание {{ 256 }} ТЗ 224 Тема 1-5-0

Фаза гармонических колебаний не зависит от:

£ положения колеблющегося маятника в данный момент времени

£ частоты колебаний

+ периода колебаний

£ амплитуды колебаний

£ времени

Задание {{ 257 }} ТЗ 225 Тема 1-5-0

Интенсивность волны не зависит от:

+ энергии, переносимой механической волной

£ площади поверхности, пересекаемой механической волной

£ ориентации поверхности, пересекаемой механической волной

£ потока энергии, переносимой механической волной

£ упругости среды, в которой распространяется механическая волна

Задание {{ 258 }} ТЗ 226 Тема 1-5-0

Неверным является выражение для скорости распространения механической волны:

£ v

+ v

£ V/n=l

МЕХАНИЧЕСКИЕ ВОЛНЫ

Задание {{ 54 }} ТЗ 39 Тема 1-3-0

В выражении для смещения материальной точки в случае гармонических колебаний, символ S означает:

£ амплитуду колебаний

£ фазу волны

£ расстояние между соседними гребнями волн

£ произвольную координату

+ смещение точки, участвующей в волновом процессе

Задание {{ 55 }} ТЗ 40 Тема 1-3-0

В уравнении волны символ x представляет собой:

£ смещение точки, участвующей в волновом процессе

+ произвольную координату

£ амплитуду колебаний

£ фазу волны

£ расстояние между соседними гребнями волн

Задание {{ 56 }} ТЗ 41 Тема 1-2-0

Длиной волны называется:

£ расстояние между двумя соседними точками на оси OX, колеблющимися в одинаковых фазах

+ расстояние между двумя соседними точками на оси OY, колеблющимися в одинаковых фазах

£ расстояние между двумя соседними точками на оси OX, колеблющимися в противоположных фазах

£ расстояние, пробегаемое волной за единицу времени

£ наибольшее отклонение точек волны от положения равновесия

Задание {{ 57 }} ТЗ 42 Тема 1-4-0

Неподвижные точки, существующие в стоячей волне, называются:

£ пучностями

£ фронтом

+ узлами

£ фазой

£ начальной координатой

Задание {{ 58 }} ТЗ 43-Тема 1-3-0

Множество точек, имеющих одновременно одинаковую фазу, называют:

£ границей волны

£ потоком волны

+ фронтом волны

£ поверхностью волны

£ фазой волны

Задание {{ 59 }} ТЗ 44 Тема 1-3-0

Энергия, переносимая упругой волной:

+ складывается из потенциальной энергии деформации и кинетической энергии колеблющихся частиц

£ определяется только потенциальной энергии деформации упругой среды

£ определяется только кинетической энергии колеблющихся частиц

£ определяется только скоростью ее распространения

£ определяется только упругими свойствами среды, в которой она распространяется

Задание {{ 60 }} ТЗ 45 Тема 1-4-0

Как в поперечных, так и в продольных волнах:

£ Энергия переносится только в поперечных волнах

+ перенос вещества осуществляется только в направлении распространения волны

£ переноса вещества в направлении распространения волны не происходит

£ перенос вещества в направлении распространения волны имеет место только в упругих средах

£ не происходит переноса энергии

Задание {{ 61 }} ТЗ 46 Тема 1-4-0

Вектором Умова называют:

+ величину, равную потоку энергии волн, проходящему через единичную площадь, перпендикулярную этому направлению

£ вектор, перпендикулярный направлению распространения волны

£ величину, равную плотности энергии волны

£ величину кинетической энергии, переносимой волной

£ величину, показывающую скорость затухания волны

Задание {{ 62 }} ТЗ 48 Тема 1-4-0

Вектор Умова определяется выражением:

Задание {{ 63 }} ТЗ 47 Тема 1-4-0

Вектор Умова определяется выражением .В этой формуле величина Ф представляет собой:

£ интенсивность волны

£ амплитуду волны

+ поток энергии волн

£ плотность энергии волн

£ энергию волн

Задание {{ 64 }} ТЗ 47 Тема 1-4-0

Поток энергии волн Ф может быть записана в виде:

Задание {{ 65 }} ТЗ 49 Тема 1-4-0

Для потока энергии волн величина w_p представляет собой:

+ объемную плотность энергии колебательного движения

£ скорость распространения волны

£ круговую частоту волны

£ фазу волны

£ амплитуду волны

Задание {{ 66 }} ТЗ 51 Тема 1-4-0

Величина w_pв формуле для потока энергии волн измеряется в:

£ Вт

£ Дж/м²

£ Дж

£ Дж/м

+ Вт/м²

Задание {{ 68 }} ТЗ 52 Тема 1-4-0

В стоячей волне:

£ переносится только потенциальная энергия

£ переносится только кинетическая энергия

£ переносится как потенциальная, так и кинетическая энергия

£ энергия волны рассеивается в упругой среде

+ отсутствует перенос энергии

Задание {{ 69 }} ТЗ 53 Тема 1-4-0

Волновым числом называют выражение:

Задание {{ 70 }} ТЗ 54 Тема 1-4-0

Волны, имеющие одинаковую разность фаз, называются:

+ когерентными

£ стоячими

£ продольными

£ поперечными

£ бегущими

Задание {{ 52 }} ТЗ 38 Тема 1-3-0

Механической волной называется:

£ механические колебания, описываемые по гармоническому закону

£ механическое возмущение, возникающее в твердом теле при его деформации

£ перенос энергии в упругой среде

+ механическое возмущение, распространяющееся в пространстве и несущее энергию

£ периодическое отклонение тела от положения равновесия

Задание {{ 53 }} ТЗ 38 Тема 1-3-0

Уравнение волны записывается в следующем виде:

Задание {{ 259 }} ТЗ 50 Тема 1-4-0

Скорость распространения волны определяется выражением:

Раздел 2.ТЕРМОДИНАМИКА

ЭФФЕКТ ДОПЛЕРА

Задание {{ 86 }} ТЗ 65 Тема 1-3-0

Эффект Доплера заключается в изменении:

£ скорости распространения волн, воспринимаемых наблюдателем, при относительном движения источника волн и наблюдателя

+ частоты волн, воспринимаемых наблюдателем, вследствие относительного движения источника волн и наблюдателя

£ громкости звука, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника

£ интенсивности волн, воспринимаемых наблюдателем, вследствие относительного движения источника звука и приемника

£ фазы сигнала, воспринимаемого наблюдателем, вследствие относительного движения источника звука и приемника

Задание {{ 87 }} ТЗ 66 Тема 1-3-0

Эффект Доплера наблюдается:

£ только для ультразвука

£ только для света

£ только для звука

£ только для электромагнитных волн

+ для любых волн

Задание {{ 88 }} ТЗ 67 Тема 1-3-0

Эффект Доплера описывается выражением:

Задание {{ 89 }} ТЗ 68 Тема 1-3-0

В формуле для эффекта Доплера символ ν₀ означает:

£ длину волны сигнала, испускаемого источником

£ скорость распространения сигнала в среде

+ частоту сигнала, испускаемого источником

£ скорость движения источника сигнала

£ амплитуду колебаний звуковой волны

Задание {{ 90 }} ТЗ 68 Тема 1-5-0

В гемодинамике УЗ эффект Доплера применяется для:

£ определения диаметра кровеносных сосудов

+ определения скорости кровотока

£ изучения распределения фармпрепаратов в организме человека

£ определения скорости оседания эритроцитов

£ визуализации внутренних органов человека

Задание {{ 91 }} ТЗ 69 Тема 1-5-0

В кардиологии УЗ эффект Доплера позволяет определить:

£ нарушения режима работы СА-узла

£ характер помех, возникающих при записи электрокардиограмм

£ изменение сечения аорты

£ визуализации желудочков сердца

+ клапанные нарушения сердца

ИДЕАЛЬНЫЙ ГАЗ

Задание {{ 92 }} ТЗ 70 Тема 1-5-0

Идеальным газом называют воображаемый газ, молекулы которого:

+ представляют собой упругие материальные точки, не связанные друг с другом межмолекулярными силами сцепления

£ имеют пренебрежимо малые размеры и находятся в неподвижном состоянии

£ имеют размеры, сопоставимые с их свободным пробегом и между которыми действуют кулоновские силы отталкивания

£ имеют пренебрежимо малые размеры и между которыми действуют только гравитационные силы

£ имеют пренебрежимо малые размеры и между которыми действуют только ядерные силы

Задание {{ 93 }} ТЗ 71 Тема 1-5-0

Установить соответствие между названием процесса и его характеристикой:

Изотермический	Процесс изменения давления газа в зависимости от объема, протекающий при неизменной температуре
Изобарический	Процесс изменения объема газа в зависимости от температуры, протекающий при неизменном давлении
Изохорический	Процесс изменения давления газа в зависимости от температуры, протекающий при неизменном объеме
Адиабатический	Процесс, протекающий при отсутствии теплообмена между системой и окружающей средой
Политропический	Обратимый термодинамический процесс изменения состояния идеального газа , удовлетворяющий уравнению
Тепловой процесс (теплопередача)	Процесс изменения внутренней энергии, обусловленный ее передачей в результате теплового движения молекул без совершения работы внешними силами

Задание {{ 94 }} ТЗ 72 Тема 1-5-0

Установить соответствие между названием процесса и его уравнением:

Изотермический
Изобарический
Изохорический
Адиабатический

Задание {{ 95 }} ТЗ 73 Тема 1-5-0

Установить соответствие между уравнением экспериментального газового закона и его названием:

Менделеева-Клапейрона
Гей-Люссака
Бойля-Мариотта
Шарля
Пуассона

Задание {{ 96 }} ТЗ 74 Тема 1-5-0

Установить соответствие между физическими величинами, характеризующими состояние идеального газа, и их размерностью:

Давление
Универсальная газовая постоянная
Температура
Объем

Задание {{ 97 }} ТЗ 75 Тема 1-5-0

Установить соответствие между элементами:

Величина давления газа	Прямо пропорционально средней кинетической энергии поступательного движения молекул, содержащихся в единице объема газа.
Средняя кинетическая энергия поступательного движения молекулы идеального газа	Пропорциональна абсолютной температуре и зависит только от нее
Внутренняя энергия любой массы газа	Пропорциональна числу степеней свободы молекулы, абсолютной температуре и массе газа
Универсальная газовая постоянная	Численно равна работе по расширению моля идеального газа при нагревании его на 1 К
Средняя квадратичная скорость молекул	Пропорциональна корню квадратному из абсолютной температуры и зависит только от нее

Задание {{ 169 }} ТЗ 140 Тема 1-5-0

Внутренняя энергия идеального газа зависит только от его:

£ объема и не зависит от температуры

£ давления и не зависит от температуры

+ температуры и не зависит от объема

£ объема и не зависит от давления

£ давления и не зависит от объема

Задание {{ 170 }} ТЗ 141 Тема 1-5-0

Внутренняя энергия идеального газа зависит только от его температуры и не зависит от объема. Это утверждение известно в термодинамике как закон:

£ Кулона

£ Джоуля

+ Больцмана

£ Клаузиуса

£ Карно

Задание {{ 171 }} ТЗ 142 Тема 1-5-0

Внутренняя энергия одного моля идеального одноатомного газа (гелий, неон и др.), молекулы которого совершают только поступательное движение, равна:

Задание {{ 172 }} ТЗ 137 Тема 1-5-0

В общем случае при переходе из некоторого начального состояния (1) в конечное состояние (2) работа газа выражается формулой:

Задание {{ 173 }} ТЗ 228 Тема 1-5-0

Работа газа численно равна площади под графиком процесса на диаграмме:

£ (V,T)

£ (A,T)

+ (p, V)

£ (p,T)

£ (R,T)

Задание {{ 174 }} ТЗ 139 Тема 1-5-0

В соответствии с первым законом термодинамики количество теплоты, полученное системой:

£ Идет на изменение ее давления и не зависит от изменения температуры

+ Идет на изменение ее внутренней энергии и совершение работы:

£ Зависит только от изменения ее объема и не зависит от изменения температуры

£ Идет на совершение работы и не зависит от изменения ее внутренней энергии

£ Идет на изменение ее внутренней энергии и не зависит от совершения работы

Задание {{ 175 }} ТЗ 140 Тема 1-5-0

В изохорном процессе:

£ Количество теплоты, подводимое к системе, полностью затрачивается на совершение работы

£ Первый закон термодинамики записывается в виде Q = U(T₂) – U(T₁) + p(V₂ – V₁) = ΔU + pΔV

£ Температура газа не изменяется, т.е. не изменяется и его внутренняя энергия: ΔU = 0

+ Газ работы не совершает, следовательно, Q = ΔU = U(T₂) – U(T₁)

£ Работа, совершаемая газом, выражается соотношением A = p(V₂ – V₁) = pΔV

Задание {{ 176 }} ТЗ 141 Тема 1-5-0

В изобарном процессе:

£ Температура газа не изменяется, т.е. не изменяется и его внутренняя энергия: ΔU = 0

£ Первый закон термодинамики записывается в виде Q = ΔU

£ Количество теплоты, подводимое к системе, полностью затрачивается на совершение работы

£ Газ работы не совершает, следовательно, Q = ΔU = U(T₂) – U(T₁)

+ Работа, совершаемая газом, выражается соотношением A = p(V₂ – V₁) = pΔV

Задание {{ 177 }} ТЗ 142 Тема 1-5-0

В изотермическом процессе:

£ Газ работы не совершает, следовательно, Q = ΔU = U(T₂) – U(T₁)

£ Q = 0, поэтому первый закон термодинамики принимает вид A = –ΔU, т. е. газ совершает работу за счет убыли его внутренней энергии

£ Первый закон термодинамики записывается в виде Q = ΔU

+ Температура газа не изменяется, также не изменяется и внутренняя энергия газа, т.е. ΔU = 0

£ Количество теплоты, подводимое к системе, полностью затрачивается на совершение работы

Задание {{ 178 }} ТЗ 143 Тема 1-5-0

В адиабатическом процессе:

£ Температура газа не изменяется, также не изменяется и внутренняя энергия газа, т.е. ΔU = 0

£ Газ работы не совершает, следовательно, Q = ΔU = U(T₂) – U(T₁)

£ Первый закон термодинамики записывается в виде Q = ΔU

£ Количество теплоты, подводимое к системе, полностью затрачивается на совершениеработы

+ Q = 0; поэтому первый закон термодинамики принимает вид A = –ΔU, т. е. газ совершает работу

за счет убыли его внутренней энергии

Задание {{ 179 }} ТЗ 144 Тема 1-5-0

Уравнение адиабатического процесса в координатах (p, V) имеет вид:

+ pV^γ = const

Задание {{ 180 }} ТЗ 229 Тема 1-5-0

В термодинамике соотношение известно как уравнение:

£ Пуассона

£ Больцмана

£ Клаузиуса

£ Карно

+ Менделеева-Клайперона

Задание {{ 181 }} ТЗ 145 Тема 1-5-0

Работа газа в адиабатическом процессе определяется выражением:

Задание {{ 182 }} ТЗ 146 Тема 1-5-0

Изменение энтропии в каком-либо квазистатическом процессе равно:

+ Приведенному теплу , полученному системой

£ Работе, совершаемой над системой

Задание {{ 183 }} ТЗ 147 Тема 1-5-0

Соотношение, выражающее связь между молярными теплоемкостями C_p и C_V, имеет вид:

Задание {{ 184 }} ТЗ 148 Тема 1-5-0

£ Джоуля

£ Больцмана

£ Клаузиуса

+ Майера

£ Карно

Задание {{ 185 }} ТЗ 148 Тема 1-5-0

Энтропия S системы и термодинамическая вероятность W связаны между собой соотношением:

Задание {{ 186 }} ТЗ 149 Тема 1-5-0

£ Джоулем

£ Клаузиусом

£ Майером

+ Больцманом

£ Карно

Задание {{ 187 }} ТЗ 150 Тема 1-5-0

В соответствии со вторым законом термодинамики:

£ Для всех термодинамических процессов справедливо соотношение:

£ Все термодинамические процессы являются обратимыми

£ Все термодинамические процессы являются необратимыми

+ Невозможен процесс, единственным результатом которого была бы передача энергии путем теплообмена от тела с низкой температурой к телу с более высокой температурой

£ Количество теплоты, полученное системой при обратимом процессе, идет на совершение работы и не зависит от изменения ее внутренней энергии

Задание {{ 188 }} ТЗ 151 Тема 1-5-0

Формулировка 2-го закона термодинамики была впервые дана:

£ Джоулем

+ Клаузиусом

£ Больцманом

£ Карно

Раздел 3. МОДЕЛИ КРАВООБРАЩЕНИЯ

Задание {{ 98 }} ТЗ 76 Тема 1-5-0

Гидродинамическая модель кровеносной системы была разработана:

£ Пуазейлем

£ Эйнтховеном

+ Франком

£ Дебекки

£ Павловым

Задание {{ 99 }} ТЗ 77 Тема 1-5-0

Гидродинамическая модель кровеносной системы Франка устанавливает связь между:

£ систолическим давлением и диаметром сосудов

£ систолическим давлением, скоростью кровотока и диаметром сосудов

+ ударным объемом крови, гидравлическим сопротивлением периферической части системы кровообращения и изменением давления в артериях

£ ударным объемом крови, гидравлическим сопротивлением системы кровообращения и скоростью пульсовой волны

£ артериальным и венозным давлением

Задание {{ 100 }} ТЗ 78 Тема 1-5-0

Артериальная часть системы кровообращения моделируется:

£ жесткой трубкой

+ упругим резервуаром

£ двухкамерным резервуаром с соединительным клапаном

£ трехкамерным резервуаром с эластичной трубкой

£ жестким резервуаром с жесткой трубкой

Задание {{ 102 }} ТЗ 79 Тема 1-5-0

В выражении V=Vо+kp символ k означает:

£ Диаметр сосуда

+ Эластичность резервуара

£ Скорость кровотока

£ Ударный объем крови

£ Плотность крови

Задание {{ 162 }} ТЗ 134 Тема 2-5-0

Объемная скорость кровотока определяется выражением:

Задание {{ 163 }} ТЗ 135 Тема 1-5-0

Задание {{ 164 }} ТЗ 136 Тема 1-5-0

£ ударный объем крови за период систолы

£ разность артериального и венозного давлений в кровеносной системе

£ объемную скорость кровотока

+ гидравлическое сопротивление периферической части системы кровообращения

£ плотность крови

Задание {{ 165 }} ТЗ 137 Тема 1-5-0

Скорость пульсовой волны определяется формулой:

£ Бернулли

+ Моенса-Кортевега

£ Менделеева-Клапейрона

£ Пуазейля

£ Стокса

Задание {{ 166 }} ТЗ 138 Тема 1-5-0

Математически формула Моенса- Кортевега для скорости пульсовой волны записывается в виде:

Задание {{ 167 }} ТЗ 138 Тема 1-5-0

В формуле Моенса-Кортевега для скорости пульсовой волны пропущен символ:

Задание {{ 168 }} ТЗ 139 Тема 1-5-0

В формуле Моенса-Кортевега для скорости пульсовой волны символ означает:

£ толщину стенок сосуда

£ диаметр сосуда

£ модуль упругости вещества сосуда

£ плотность крови

+ плотность вещества сосуда

Задание {{ 104 }} ТЗ 81 Тема 1-5-0

Отметьте правильный ответ

В выражении Q=Q_с пропущен символ:

£ C

+ p

£ l

£ X₀

£ ρ

Задание {{ 106 }} ТЗ 83 Тема 1-5-0

Отметьте правильный ответ

Скорость пульсовой волны определяется формулой:

£ Бернулли

£ Моенса-Кортевега

£ Менделеева-Клапейрона

£ Стокса

+ Пуазейля

Задание {{ 107 }} ТЗ 84 Тема 1-5-0

Отметьте правильный ответ

Скорость пульсовой волны математически записывается в виде:

Задание {{ 108 }} ТЗ 85 Тема 1-5-0

Отметьте правильный ответ

£ m

£ h

+ f

£ k

£ z

Задание {{ 156 }} ТЗ 129 Тема 1-5-0

Установить соответствие между названием процесса и его диаграммой:

Изотермический
Изобарический
Изохорический

Задание {{ 261 }} ТЗ 79 Тема 1-5-0

Зависимость объема крови в резервуаре от давления определяется соотношением:

Раздел 4. МЕХАНИКА

Задание {{ 112 }} ТЗ 89 Тема 1-5-0

Начальная фаза колебаний материальной точки равна:

Задание {{ 113 }} ТЗ 90 Тема 1-5-0

Фаза колебаний в момент времени t=0,5 с равна:

Задание {{ 114 }} ТЗ 91 Тема 1-5-0

Смещение материальной точки в момент времени t=2с равно:

£ 0,5

+ 0,25

£ 0

£ 1

Задание {{ 115 }} ТЗ 92 Тема 1-5-0

Максимальная скорость колебаний материальной точки равна:

Далее ⇒