Методика построения простой группировки
Содержание
Введение. 4
1. Методика построения простой группировки. 5
2. Индекс постоянного состава, переменного и структурных сдвигов, взаимосвязь индексов. 11
3. Методы расчета ВВП.. 15
4. Система частных показателей эффективности. 18
Задача. 22
Заключение. 24
Список литературы.. 25
Введение
Гуманитарные и естественные науки в процессе исследования широко применяют методы статистики для сбора, обработки и анализа данных. Для разработки предмета статистики применяются специальные приемы и методы, совокупность которых образует методологию статистики.
Одной из основных задач статистики является освещение социально-экономического положения РФ. Наличие полной информации о происходящих процессах и явлениях.
Предметом статистики является количественное измерение становления многоукладной экономики, с целью получения информации о качественных показателях различных форм хозяйствования с тем, чтобы проводить сопоставительный анализ их деятельности.
Основные задачи статистики:
- изучение уровня и структуры взаимосвязей динамики массовых экономических явлений и процессов;
- обобщение и прогнозирование тенденции развития экономики;
- выявление резервов повышения эффективности общественного производства;
- своевременное обеспечение информацией законодательную и исполнительную власть.
Цель курсовой работы – закрепить и углубить знания, приобретенные в процессе изучения основных разделов дисциплины статистики.
Задачи включают в себя рассмотрение следующих вопросов:
1. Методика построения простой группировки .
2. Индекс постоянного состава, переменного и структурных сдвигов, взаимосвязь индексов.
3. Методы расчета ВВП.
4. Система частных показателей эффективности.
Также будет решена задача.
Методика построения простой группировки
Изучаемые статистикой массовые явления и процессы протекают в качественно однородных совокупностях. Однако качественная однородность единиц, составляющих совокупность, не является чем-то абсолютным, навсегда и на все случаи заданным. Единицы, качественно однородные в одном отношении, оказываются разнородными в другом. Это позволяет делить статистическую совокупность на частные подсовокупности - группы.
Группировка - это разбиение совокупности на группы, однородные по какому-либо признаку. С точки зрения отдельных единиц сово совокупности группировка суть объединение отдельных единиц совокупности в группы, однородные по каким-либо признакам.
Классификация основывается на самых существенных признаках, которые меняются очень незначительно (например, классификация отраслей народного хозяйства, классификация основных фондов и т. д.). Таким образом, классификация - это узаконенная, общепринятая, нормативная группировка. Классификации стандартны, устойчивы, т. е. остаются неизменными в течение длительного периода времени, и, как правило, разрабатываются органами государственной и международной статистики.
Метод группировки основывается на двух категориях - группировочном признаке и интервале.
Типологическая группировка решает задачу выявления и характеристики социально-экономических типов (частных подсовокупностей).
Структурная дает возможность описать составные части совокупности или строение типов, а также проанализировать структурные сдвиги.
Аналитическая (факторная) группировка позволяет оценивать связи между взаимодействующими признаками. Признаки принято делить на факторные и результативные. Факторными называются признаки, оказывающие влияние на изменение результативных. Результативными называются признаки, изменяющиеся под влиянием факторных. Взаимосвязь проявляется в том, что с возрастанием значения факторного признака систематически возрастает или убывает значение признака результативного.
Различают простые и многомерные группировки.
Группировка, выполненная по одному признаку, называется простой. Многомерная группировка производится по двум и более признакам.
Построение статистических группировок проходит следующие этапы:
Ÿ выбор группировочного признака;
Ÿ определение необходимого числа групп, на которые необходимо разбить изучаемую совокупность;
Ÿ установление границ интервалов группировки;
Ÿ установление для каждой группировки показателей или их системы, которыми должны характеризоваться выделенные группы.
Выбор группировочного признака является одним из существенных и сложных вопросов теории статистической группировки и статистического исследования в целом. Группировочным называется признак, по которому осуществляется разбиение единиц совокупности на отдельные группы. От правильного выбора группировочного признака зависят выводы статистического исследования. В качестве основания группировки необходимо использовать признаки, наиболее полно отражающие сущность изучаемых социально-экономических явлений и процессов в условиях поставленных целей и задач.
В основание группировки могут быть положены как количественные, так и атрибутивные признаки.
Построение группировки по атрибутивному признаку требует правильного определения его градаций, на основе которых устанавливается принадлежность изучаемых явлений и процессов к определенному виду. При этом выделенные группы отличаются друг от друга не по величине признака, а по качественной характеристике признака. Число групп, на которые разбивается изучаемая совокупность, как правило, определяется числом градаций атрибутивного признака. Так, например, группировка женщин по семейному положению предполагает образование только двух групп – «замужем» и «не замужем». Группировка предприятий по формам собственности учитывает муниципальную, федеральную и собственность субъектов Федерации.
Число групп зависит от задач исследования и вида показателя, положенного в основание группировки, объема совокупности – числа единиц исследуемого объекта, степени вариации группировочного признака.
Учет объема изучаемой совокупности предполагает установление такого количества групп, чтобы достаточно четко и определенно выявился характер распределения и особенности изучаемого явления. При небольшом объеме совокупности не следует образовывать большое количества групп, так как группы будут включать недостаточное число единиц. Поэтому показатели, рассчитанные для таких групп, не будут представительными и типичными и не позволят получить адекватную характеристику исследуемого социально-экономического явления.
Часто группировка по количественному признаку имеет задачу отразить распределение единиц совокупности по этому признаку. В этом случае количество групп зависит в первую очередь от степени колеблемости группировочного признака: чем больше колеблемость признака, тем больше можно образовать групп. В этом случае целесообразно рассматривать размах вариации, который определяется как разность между максимальным и минимальным значениями признака. Чем больше размах варьирования признака, положенного в основание группировки, тем, как правило, больше может быть образовано групп. Ограничением здесь является наполняемость групп элементами изучаемой совокупности.
Чем больше образовано групп, тем точнее будет воспроизведен характер исследуемого объекта. Однако слишком большое число групп затрудняет выявление закономерностей при исследовании социально-экономических явлений и процессов. Поэтому в каждом конкретном случае при определении числа групп следует исходить не только из степени вариации признака, но и из особенностей объекта, цели и задач исследования.
Определение числа групп можно осуществить и математическим путем с использованием формулы Стерджесса
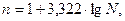
где п – число групп; N – число единиц совокупности; lgN -десятичный логарифм от N.
Согласно этой формуле выбор числа групп зависит от объема совокупности.
Недостаток формулы состоит в том, что ее применение дает хорошие результаты, только если совокупность состоит из большого числа единиц. При определении числа групп данным методом существует большая вероятность получения «пустых» или малочисленных групп. «Пустыми» называются группы, которые не содержат ни одной единицы совокупности.
После того как определено число групп, следует решить задачу определения интервалов группировки.
Интервал группировки определяет границы значений варьирующего признака, лежащих в пределах определенной группы. Каждый интервал имеет свою длину (ширину), верхнюю и нижнюю границы или хотя бы одну из них.
Нижней границей интервала называется наименьшее значение признака в интервале. Верхней границей интервала называется наибольшее значение признака в интервале. Нижней границей первого интервала берется, как правило, наименьшее значение признака в совокупности единиц наблюдения. Верхняя граница последнего интервала не может быть меньше наибольшего значения признака в совокупности единиц наблюдения.
Величиной (шириной) интервала называется разность между верхней и нижней границами.
Интервалы группировки в зависимости от их ширины бывают равные и неравные. Последние делятся на прогрессивно возрастающие, прогрессивно убывающие, произвольные и специализированные.
Если вариация признака проявляется в сравнительно узких границах и распределение носит равномерный характер, то строят группировку с равными интервалами. Ширина равного интервала ( h ) определяется по формуле

где  ,
,  - максимальное и минимальное значения признака в совокупности; п – число групп.
- максимальное и минимальное значения признака в совокупности; п – число групп.
Полученную по формуле величину округляют, и она будет являться шагом интервала.
Если размах вариации признака в совокупности велик и значения признака варьируют неравномерно, то надо использовать группировку с неравными интервалами. Неравные интервалы могут быть получены несколькими способами. В случае, если построенная группировка с равными интервалами содержит группы, не отражающие определенные типы изучаемого явления или процесса или не содержащие ни одной единицы совокупности, то возникает необходимость увеличении - объединения двух или нескольких малочисленных или «пустых» последовательных равных интервалов.
Другим способом построения неравных интервалов является применение прогрессивно возрастающих и прогрессивно убывающих интервалов, в основе построения которых лежит принцип арифметической или геометрической прогрессии. Величина интервалов, изменяющихся в арифметической прогрессии, определяется по формуле
 ,
,
где а – константа: для прогрессивно возрастающих интервалов имеет знак « + » и знак « - » для прогрессивно убывающих;  величина i-го интервала;
величина i-го интервала;
а в геометрической прогрессии:
 ,
,
где q - константа: >1 - для прогрессивно возрастающих и <1 - для прогрессивно убывающих интервалов.
Применение неравных интервалов обусловлено спецификой и особенностями изучаемого социально-экономического явления или процесса, когда в первых группах небольшая разница в показателях имеет большое значение, а в последних группах эта разница существенного значения не имеет. Например, при построении группировки страховых компаний по численности работающих, которая варьируется от 30 до 1010 чел., нецелесообразно рассматривать равные интервалы, так как при этом учитываются как малые, так и крупнейшие страховые компании. Поэтому следует образовывать неравные интервалы: 30–200, 200–540, 540–1050, т. е. величина каждого последующего и интервала больше предыдущего на 170 чел. и увеличивается в арифметической прогрессии.
Решение вопроса о выборе равных или неравных интервалов зависит от числа единиц совокупности, попавших в каждую выделенную группу, т.е. от степени заполнения интервалов.
Интервалы группировок могут быть закрытыми и открытыми. Закрытыми называются интервалы, в которых указаны верхняя и нижняя границы. Открытыми называются интервалы, у которых указана только одна граница: верхняя – у первого, нижняя – у последнего. Например, группы консалтинговых компаний по числу работающих в них сотрудников: до 100, 100–200, 200–300, 300 чел. и более.
При изучении социально-экономических явлений на макроуровне часто применяют группировки, интервалы которых не будут ни прогрессивно возрастающими, ни прогрессивно убывающими. Такие интервалы называются произвольными и, как правило, используются при группировке предприятий, например, по уровню рентабельности.