Тема 1. Работа с массивами
1.1 Простейшие операции над матрицами
Пример 1. - Умножение массива А1:В2 на число 5:
1) В ячейку В2 ввел формулу =3*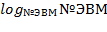 
;
2) В ячейку А2 – формулу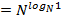 
;
3) Выделил на рабочем листе область D1:E2 и ввел формулу =А1:В2*5 и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =A1:B2*5 | =A1:B2*5 | |||
| =СТЕПЕНЬ(78;LOG(1;78)) | =3*LOG(10;10) | =A1:B2*5 | =A1:B2*5 |
Пример 2. – Сумма (разность) массивов.
1) В ячейку В2 ввел формулу =2* ;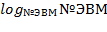
2) В ячейку А2 ввел формулу = 
;
3) Выделил ячейки G1:H2 ввел формулу =A1:B2+D1:E2 и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =A1:B2+D1:E2 | =A1:B2+D1:E2 | ||||||
| =СТЕПЕНЬ(78;LOG(3;78)) | = 2*LOG(10;10) | =A1:B2+D1:E2 | =A1:B2+D1:E2 |
Пример 3. – Поэлементное произведение (деление) массивов.
1) Выделил ячейки G1:H2 ввел формулу =A1:B2*D1:E2 и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =A1:B2*D1:E2 | =A1:B2*D1:E2 | ||||||
| =СТЕПЕНЬ(78;LOG(3;78)) | = 2*LOG(10;10) | =A1:B2*D1:E2 | =A1:B2*D1:E2 |
1.2. Встроенные функции для работы с матрицами
Пример 5. Решим систему линейных уравнений с двумя неизвестными:
Чтобы решить данную систему линейных уравнений AX=B, где А – матрица коэффициентов системы, X – вектор-столбец неизвестных, В – вектор-столбец из свободных членов. а X = 
, где 
обратная матрица А, поэтому для решения этой системы уравнений проведем следующие операции:
1) Выделим ячейки F1:F2 и введем следующую формулу =МУМНОЖ(МОБР(A1:B2);D1:D2) и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =МУМНОЖ(МОБР(A1:B2);D1:D2) | |||||
| =МУМНОЖ(МОБР(A1:B2);D1:D2) |
| 2,166666667 | |||||
| -1,333333333 |
Пример 6. Решить систему линейных уравнений 
, где
А= 
, B= 
Для решения этой матрицы проведем следующие операции:
1) Введем в диапазон ячеек А1:В2 элементы матрицы А;
2) Введем в диапазон ячеек D1:D2 – элементы столбца свободных членов В;
2) Выделим диапазон F1:F2 куда введем следующую формулу =МУМНОЖ(МОБР(МУМНОЖ(A1:B2;A1:B2));D1:D2) и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =СТЕПЕНЬ(78;LOG(7;78)) | =МУМНОЖ(МОБР(МУМНОЖ(A1:B2;A1:B2));D1:D2) | ||||
| =LOG(10;10) | =МУМНОЖ(МОБР(МУМНОЖ(A1:B2;A1:B2));D1:D2) |
| 0,020710059 | |||||
| 0,042899408 |
Пример 7. Вычисление квадратичной формулы z= 
, где А – квадратичная матрица, введенная в диапазон А1:В2; Х – вектор, введенный в диапазон D1:D2, а символ (т) обозначает операцию транспонирования (все данные из примера 5). Для вычисления данной формулы введем в ячейку F1 формулу -=МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);A1:B2);D1:D2) – получаем:
| =МУМНОЖ(МУМНОЖ(ТРАНСП(D1:D2);A1:B2);D1:D2) | |||||
Пример 8. Вычисление значения квадратичной формы Z= 
, где
А= , Y=
Для решения этой задачи надо ввести в диапазон ячеек А1:В2 элементы матрицы А, в диапазон D1:D2 элементы столбца Y, в ячейку F1 нужно ввести формулу =МУМНОЖ(ТРАНСП(D1:D2);МУМНОЖ(ТРАНСП(A1:B2);D1:D2)):
| =СТЕПЕНЬ(78;LOG(7;78)) | =МУМНОЖ(ТРАНСП(D1:D2);МУМНОЖ(ТРАНСП(A1:B2);D1:D2)) | ||||
| =LOG(10;10) |
Задание 1. Решить системы линейных уравнений AX=B, 
и вычислить значение квадратичной формы Z= 
, где
А= 
, В= 
, Y= 
Решение формы AX=B:
1) В диапазон A1:D4 ввел значения матрицы А;
2) В диапазон F1:F4 ввел значения столбца В;
3) В ячейку Н1 ввел формулу =МУМНОЖ(МОБР(A1:D4);F1:F4) и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =МУМНОЖ(МОБР(A1:D4);F1:F4) | |||||||
| -0,735189016 | |||||||
Решение формы 
Х=В:
В ячейку Н1 ввел формулу =МУМНОЖ(МОБР(МУМНОЖ(МУМНОЖ(A1:D4;A1:D4);A1:D4));F1:F4) и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =МУМНОЖ(МОБР(МУМНОЖ(МУМНОЖ(A1:D4;A1:D4);A1:D4));F1:F4) | |||||||
| 0,013795645 | |||||||
Решение формы Z= 
:
В ячейку J1 ввел формулу =МУМНОЖ(МУМНОЖ(ТРАНСП(H1:H4);ТРАНСП(A1:D4));МУМНОЖ(МУМНОЖ(A1:D4;A1:D4);H1:H4)) и закончил ввод нажатием следующих цифр – <Ctrl>+<Shift>+<Enter> - и получил следующий результат:
| =МУМНОЖ(МУМНОЖ(ТРАНСП(H1:H4);ТРАНСП(A1:D4));МУМНОЖ(МУМНОЖ(A1:D4;A1:D4);H1:H4)) | |||||||||
1.3 Пошаговое решение системы линейных уравнений методом Гаусса.
1) В столбец A1:D4 и E1:E4 введены матрицы коэффициентов и столбец членов соответственно;
2) Скопировал содержимое ячеек А1:Е! в ячейки А6:Е6, А1:Е11, А16:Е16;
3) В диапазоне ячеек А7:Е7 ввел формулу {=A2:E2-$A$1:$E$1*(A2/$A$1)};
4) Выделил диапазон А7:Е7 и протащил маркер так, чтобы заполнить диапазон А7:Е9;
5) Скопировал значения ячеек из диапазона А7:Е7 в диапазоны А12:Е12 и А17:Е17;
6) В ячейки А13:Е13 ввел формулу =A8:E8-$A$7:$E$7*(B8/$B$7);
7) Выделил диапазон А13:Е13 и протащил маркер так, чтобы заполнить диапазон А13:Е14;
8) Скопировал значения ячеек из диапазона А13:Е13 в диапазоны А18:Е18;
9) В диапазон ячеек А19:Е19 ввел формулу =A14:E14-$A$13:$E$13*(C14/$C$13);
10) В диапазоны G4:K4, G3:K3, G2:K2,G1:K1 следующие формулы соответственно:
=A19:E19/D19;
=(A18:E18-G4:K4*D18)/C18;
=(A17:E17-G4:K4*D17-G3:K3*C17)/B17;
=(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 – в результате получил:
| =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 | =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 | =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 | =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 | =(A16:E16-G4:K4*D16-G3:K3*C16-G2:K2*B16)/A16 | ||||||
| =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 | =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 | =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 | =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 | =(A17:E17-G4:K4*D17-G3:K3*C17)/B17 | ||||||
| =(A18:E18-G4:K4*D18)/C18 | =(A18:E18-G4:K4*D18)/C18 | =(A18:E18-G4:K4*D18)/C18 | =(A18:E18-G4:K4*D18)/C18 | =(A18:E18-G4:K4*D18)/C18 | ||||||
| =A19:E19/D19 | =A19:E19/D19 | =A19:E19/D19 | =A19:E19/D19 | =A19:E19/D19 | ||||||
| =A2:E2-$A$1:$E$1*(A2/$A$1) | =A2:E2-$A$1:$E$1*(A2/$A$1) | =A2:E2-$A$1:$E$1*(A2/$A$1) | =A2:E2-$A$1:$E$1*(A2/$A$1) | =A2:E2-$A$1:$E$1*(A2/$A$1) | ||||||
| =A3:E3-$A$1:$E$1*(A3/$A$1) | =A3:E3-$A$1:$E$1*(A3/$A$1) | =A3:E3-$A$1:$E$1*(A3/$A$1) | =A3:E3-$A$1:$E$1*(A3/$A$1) | =A3:E3-$A$1:$E$1*(A3/$A$1) | ||||||
| =A4:E4-$A$1:$E$1*(A4/$A$1) | =A4:E4-$A$1:$E$1*(A4/$A$1) | =A4:E4-$A$1:$E$1*(A4/$A$1) | =A4:E4-$A$1:$E$1*(A4/$A$1) | =A4:E4-$A$1:$E$1*(A4/$A$1) | ||||||
| 0,5 | -7,5 | -8 | 1,5 | |||||||
| =A8:E8-$A$7:$E$7*(B8/$B$7) | =A8:E8-$A$7:$E$7*(B8/$B$7) | =A8:E8-$A$7:$E$7*(B8/$B$7) | =A8:E8-$A$7:$E$7*(B8/$B$7) | =A8:E8-$A$7:$E$7*(B8/$B$7) | ||||||
| =A9:E9-$A$7:$E$7*(B9/$B$7) | =A9:E9-$A$7:$E$7*(B9/$B$7) | =A9:E9-$A$7:$E$7*(B9/$B$7) | =A9:E9-$A$7:$E$7*(B9/$B$7) | =A9:E9-$A$7:$E$7*(B9/$B$7) | ||||||
| 0,5 | -7,5 | -8 | 1,5 | |||||||
| -84 | -84 | |||||||||
| =A14:E14-$A$13:$E$13*(C14/$C$13) | =A14:E14-$A$13:$E$13*(C14/$C$13) | =A14:E14-$A$13:$E$13*(C14/$C$13) | =A14:E14-$A$13:$E$13*(C14/$C$13) | =A14:E14-$A$13:$E$13*(C14/$C$13) |
| 0,185714 | ||||||||||
| 0,778571 | ||||||||||
| -0,63571 | ||||||||||
| 0,457143 | ||||||||||
| 0,5 | -7,5 | -8 | 1,5 | |||||||
| -4,5 | -16,5 | -12 | 1,5 | |||||||
| -1,5 | -9,5 | -3 | 3,5 | |||||||
| 0,5 | -7,5 | -8 | 1,5 | |||||||
| -84 | -84 | |||||||||
| -32 | -27 | |||||||||
| 0,5 | -7,5 | -8 | 1,5 | |||||||
| -84 | -84 | |||||||||
| 2,285714 |
Тема2. Уравнение регрессии
2.1. общий подход к построению уравнения регрессии на примере линейной модели
Пример 9. Решение задачи нелинейной оптимизации с помощью средства поиска решений на примере линейного уравнения регрессии:
1) В ячейку В2 поместил формулу =7*LOG(10;10);
2) В ячейку А2 поместил формулу =СТЕПЕНЬ(78;LOG(1;78));
3) В ячейку F3 ввел формулу =СУММКВРАЗН(B2:B7;E2+D3*A2:A7);
4) Провел операцию Данные – Поиск решения и получил результат:
| x | y | m | b | ||
| =СТЕПЕНЬ(78;LOG(1;78)) | =7*LOG(10;10) | ||||
| 1,88571412875188 | 5,39999996034584 | =СУММКВРАЗН(B2:B7;E3+D3*A2:A7) | |||
| x | y | m | b | ||
| 1,885714 | 5,4 | 1,771428571 | |||
2.2. Функции рабочего листа для уравнения линейной регрессии
Пример 10. Определение параметров m и b с помощью функции НАКЛОН и ОТРЕЗОК:
1) Для нахождения m надо ввести в ячейку D2 формулу =НАКЛОН(B2:B7;A2:A7);
2) Для нахождения b надо ввести в ячейку E2 формулу =ОТРЕЗОК(B2:B7;A2:A7$);
3) Получил следующий результат:
| x | y | m | b | ||
| =СТЕПЕНЬ(78;LOG(1;78)) | =7*LOG(10;10) | =НАКЛОН(B2:B7;A2:A7) | =ОТРЕЗОК(B2:B7;A2:A7) | ||
| 1,88571412875188 | 5,39999996034584 | =СУММКВРАЗН(B2:B7;E3+D3*A2:A7) | |||
| x | y | m | b | ||
| 1,885714286 | 5,4 | ||||
| 1,885714129 | 5,39999996 | 1,771428571 | |||
Пример 11. Нахождение m и b с помощью точечного графика:
1) Выделил диапазон А2:В7, затем вставил точечную диаграмму (Вставка – Диаграммы – Точечная);
2) На появившуюся диаграмму щелкнул правой кнопкой мыши, в появившемся диалоговом окне выбрал команду Добавить линию тренда;
3) В диалоговом окне Линия тренда выбрал параметр – Линейная; установил флажки на пунктах Показать уравнение на диаграмме и Поместить на диаграмму величину достоверности аппроксимации;
4) Нашел теоретические значения у введя в ячейку С2 формулу =$D$2*A2+$E$2 и растянув на диапазон С2:С7:
| x | y | Теор. Значение у | m | b | |
| =СТЕПЕНЬ(78;LOG(1;78)) | =7*LOG(10;10) | =$D$2*A2+$E$2 | =НАКЛОН(B2:B7;A2:A7) | =ОТРЕЗОК(B2:B7;A2:A7) | |
| =$D$2*A3+$E$2 | 1,88571412875188 | 5,39999996034584 | =СУММКВРАЗН(B2:B7;E3+D3*A2:A7) | ||
| =$D$2*A4+$E$2 | |||||
| =$D$2*A5+$E$2 | |||||
| =$D$2*A6+$E$2 | |||||
| =$D$2*A7+$E$2 |
| x | y | Теор. Значение у | m | b | |
| 7,285714286 | 1,885714286 | 5,4 | |||
| 9,171428571 | 1,885714129 | 5,39999996 | 1,771428571 | ||
| 11,05714286 | |||||
| 12,94285714 | |||||
| 14,82857143 | |||||
| 16,71428571 |
Задание 3
1. Построение линейную модель по следующим данным:
| =НАКЛОН(A2:H2;A1:H1) | =ОТРЕЗОК(A2:H2;A1:H1) | |||||||||
| =13*LOG(10;10) | =СТЕПЕНЬ(78;LOG(55;78)) |
| 6,011904762 | 7,07142857 | |||||||||
2. Построение экспоненцианальной модели:
| =НАКЛОН(A2:H2;A1:H1) | =ОТРЕЗОК(A2:H2;A1:H1) | Теоретическое значение | ||||||||||||||||
| =13*LOG(10;10) | =СТЕПЕНЬ(78;LOG(55;78)) | =$J$1*A1+$K$1 | =$J$1*B1+$K$1 | =$J$1*C1+$K$1 | =$J$1*D1+$K$1 | =$J$1*E1+$K$1 | =$J$1*F1+$K$1 | =$J$1*G1+$K$1 | =$J$1*H1+$K$1 |
| 6,011904762 | 7,071429 | Теоретическое значение | ||||||||||||||||
| 13,08333333 | 19,09524 | 25,10714 | 31,11905 | 37,13095 | 43,14286 | 49,15476 | 55,16667 |
Тема 3. Решение нелинейных уравнений а Excel
3.1. Нахождение корней уравнения
Пример 12. Пример нахождения всех корней уравнения
1) Протабулировал полином на отрезке[1;-1] шагом 0,2 в столбце А;
2) В ячейку В2 ввел следующую формулу =A3^3-0,01*LOG(78;78)*A3^2-0,7044*A3+0,139104;
3) По получившимся результатам построил график;
4) В ячейки С2:С4 ввел приближенные значения в ячейку D2 ввел формулу =C2^3-0,01*LOG(78;78)*C2^2-0,7044*C2+0,139104 протащил на ячейки D3, D4;
5) Выполнил подбор параметра (Данные – Работа с данными – Анализ «что-если» - Подбор параметра):
| x | y | Приближение | Значение функции | |
| -1 | =A2^3-0,01*LOG(78;78)*A2^2-0,7044*A2+0,139104 | -0,919994327978423 | =C2^3-0,01*LOG(78;78)*C2^2-0,7044*C2+0,139104 | |
| -0,8 | =A3^3-0,01*LOG(78;78)*A3^2-0,7044*A3+0,139104 | 0,210000684055703 | =C3^3-0,01*LOG(78;78)*C3^2-0,7044*C3+0,139104 | |
| -0,6 | =A4^3-0,01*LOG(78;78)*A4^2-0,7044*A4+0,139104 | 0,719975360423083 | =C4^3-0,01*LOG(78;78)*C4^2-0,7044*C4+0,139104 | |
| -0,4 | =A5^3-0,01*LOG(78;78)*A5^2-0,7044*A5+0,139104 | |||
| -0,2 | =A6^3-0,01*LOG(78;78)*A6^2-0,7044*A6+0,139104 | |||
| =A7^3-0,01*LOG(78;78)*A7^2-0,7044*A7+0,139104 | ||||
| 0,2 | =A8^3-0,01*LOG(78;78)*A8^2-0,7044*A8+0,139104 | |||
| 0,4 | =A9^3-0,01*LOG(78;78)*A9^2-0,7044*A9+0,139104 | |||
| 0,6 | =A10^3-0,01*LOG(78;78)*A10^2-0,7044*A10+0,139104 | |||
| 0,8 | =A11^3-0,01*LOG(78;78)*A11^2-0,7044*A11+0,139104 | |||
| =A12^3-0,01*LOG(78;78)*A12^2-0,7044*A12+0,139104 |
| x | y | Приближение | Значение функции | |
| -1 | -0,166496 | -0,919994328 | 1,05113E-05 | |
| -0,8 | 0,184224 | 0,210000684 | -3,9422E-07 | |
| -0,6 | 0,342144 | 0,71997536 | -2,0607E-05 | |
| -0,4 | 0,355264 | |||
| -0,2 | 0,271584 | |||
| 0,139104 | ||||
| 0,2 | 0,005824 | |||
| 0,4 | -0,080256 | |||
| 0,6 | -0,071136 | |||
| 0,8 | 0,081184 | |||
| 0,424704 |
Задание 4.
Решение:
1) Протабулировал полином на отрезке[1;-1] шагом 0,2 в столбце А;
2) В ячейку В2 ввел следующую формулу =A2^3-2,92*A2^2+1,4355*A2+0,791136+10/1000;
3) По получившимся результатам построил график;
4) Получившийся график имеет одно пересечение с осью Ох = -0,4 и в ячейку С2 ввел это значение;
5) В ячейку D2ввел формулу =C2^3-2,92*C2^2+1,4355*C2+0,791136+10/1000;
6) Выполнил подбор параметра (Данные – Работа с данными – Анализ «что-если» - Подбор параметра):
| x | y | Приближение | Значение функции |
| -1 | =A2^3-2,92*A2^2+1,4355*A2+0,791136+10/1000 | -0,4 | =C2^3-2,92*C2^2+1,4355*C2+0,791136+10/1000 |
| -0,8 | =A3^3-2,92*A3^2+1,4355*A3+0,791136+10/1000 | ||
| -0,6 | =A4^3-2,92*A4^2+1,4355*A4+0,791136+10/1000 | ||
| -0,4 | =A5^3-2,92*A5^2+1,4355*A5+0,791136+10/1000 | ||
| -0,2 | =A6^3-2,92*A6^2+1,4355*A6+0,791136+10/1000 | ||
| =A7^3-2,92*A7^2+1,4355*A7+0,791136+10/1000 | |||
| 0,2 | =A8^3-2,92*A8^2+1,4355*A8+0,791136+10/1000 | ||
| 0,4 | =A9^3-2,92*A9^2+1,4355*A9+0,791136+10/1000 | ||
| 0,6 | =A10^3-2,92*A10^2+1,4355*A10+0,791136+10/1000 | ||
| 0,8 | =A11^3-2,92*A11^2+1,4355*A11+0,791136+10/1000 | ||
| =A12^3-2,92*A12^2+1,4355*A12+0,791136+10/1000 |
| x | y | Приближение | Значение функции |
| -1 | -4,55436 | -0,4 | -0,304264 |
| -0,8 | -2,72806 | ||
| -0,6 | -1,32736 | ||
| -0,4 | -0,30426 | ||
| -0,2 | 0,389236 | ||
| 0,801136 | |||
| 0,2 | 0,979436 | ||
| 0,4 | 0,972136 | ||
| 0,6 | 0,827236 | ||
| 0,8 | 0,592736 | ||
| 0,316636 |
3.2. Нахождение корней уравнения методом деления отрезка пополам
Пример 13. Нахождение корня уравнения 
с точностью до 0,001 методом деления отрезка пополам.
1) В ячейку В1 Ввел погрешность нахождения корня 0,001;
2) За первоначальный отрезок локализации принял отрезок [0;2];
3) В ячейки C3, D3, E3, A4, B4, F4 ввел необходимые формулы;
4) Получил решение:
| Точность нахождения корня | 0,001 | ||||||
| a | b | c | Проверка знака | Значение функции в средней точке | |||
| =(A3+B3)/2 | =(A3^2-2)*(C3^2-2) | =C3^2-2 | |||||
| =ЕСЛИ(D3<=0;A3;C3) | =ЕСЛИ(D3<=0;C3;B3) | =(A4+B4)/2 | =(A4^2-2)*(C4^2-2) | =C4^2-2 | =ЕСЛИ(B3-A3<$B$1;"Корень найден и равен" &СТ(C3;"0?0000");"") | ||
| =ЕСЛИ(D4<=0;A4;C4) | =ЕСЛИ(D4<=0;C4;B4) | =(A5+B5)/2 | =(A5^2-2)*(C5^2-2) | =C5^2-2 | =ЕСЛИ(B4-A4<$B$1;"Корень найден и равен" &СТ(C4;"0?0000");"") | ||
| =ЕСЛИ(D5<=0;A5;C5) | =ЕСЛИ(D5<=0;C5;B5) | =(A6+B6)/2 | =(A6^2-2)*(C6^2-2) | =C6^2-2 | =ЕСЛИ(B5-A5<$B$1;"Корень найден и равен" &СТ(C5;"0?0000");"") | ||
| =ЕСЛИ(D6<=0;A6;C6) | =ЕСЛИ(D6<=0;C6;B6) | =(A7+B7)/2 | =(A7^2-2)*(C7^2-2) | =C7^2-2 | =ЕСЛИ(B6-A6<$B$1;"Корень найден и равен" &СТ(C6;"0?0000");"") | ||
| =ЕСЛИ(D7<=0;A7;C7) | =ЕСЛИ(D7<=0;C7;B7) | =(A8+B8)/2 | =(A8^2-2)*(C8^2-2) | =C8^2-2 | =ЕСЛИ(B7-A7<$B$1;"Корень найден и равен" &СТ(C7;"0?0000");"") | ||
| =ЕСЛИ(D8<=0;A8;C8) | =ЕСЛИ(D8<=0;C8;B8) | =(A9+B9)/2 | =(A9^2-2)*(C9^2-2) | =C9^2-2 | =ЕСЛИ(B8-A8<$B$1;"Корень найден и равен" &СТ(C8;"0?0000");"") | ||
| =ЕСЛИ(D9<=0;A9;C9) | =ЕСЛИ(D9<=0;C9;B9) | =(A10+B10)/2 | =(A10^2-2)*(C10^2-2) | =C10^2-2 | =ЕСЛИ(B9-A9<$B$1;"Корень найден и равен" &СТ(C9;"0?0000");"") | ||
| =ЕСЛИ(D10<=0;A10;C10) | =ЕСЛИ(D10<=0;C10;B10) | =(A11+B11)/2 | =(A11^2-2)*(C11^2-2) | =C11^2-2 | =ЕСЛИ(B10-A10<$B$1;"Корень найден и равен" &СТ(C10;"0?0000");"") | ||
| =ЕСЛИ(D11<=0;A11;C11) | =ЕСЛИ(D11<=0;C11;B11) | =(A12+B12)/2 | =(A12^2-2)*(C12^2-2) | =C12^2-2 | =ЕСЛИ(B11-A11<$B$1;"Корень найден и равен" &СТ(C11;"0?0000");"") | ||
| =ЕСЛИ(D12<=0;A12;C12) | =ЕСЛИ(D12<=0;C12;B12) | =(A13+B13)/2 | =(A13^2-2)*(C13^2-2) | =C13^2-2 | =ЕСЛИ(B12-A12<$B$1;"Корень найден и равен" &СТ(C12;"0?0000");"") | ||
| =ЕСЛИ(D13<=0;A13;C13) | =ЕСЛИ(D13<=0;C13;B13) | =(A14+B14)/2 | =(A14^2-2)*(C14^2-2) | =C14^2-2 | =ЕСЛИ(B13-A13<$B$1;"Корень найден и равен" &СТ(C13;"0?0000");"") | ||
| =ЕСЛИ(D14<=0;A14;C14) | =ЕСЛИ(D14<=0;C14;B14) | =(A15+B15)/2 | =(A15^2-2)*(C15^2-2) | =C15^2-2 | =ЕСЛИ(B14-A14<$B$1;"Корень найден и равен" &ТЕКСТ(C14; "0,0000");" ") |
| Точность нахождения корня | 0,001 | ||||||
| a | b | c | Проверка знака | Значение функции в средней точке | |||
| -1 | |||||||
| 1,5 | -0,25 | 0,25 | |||||
| 1,5 | 1,25 | 0,4375 | -0,4375 | ||||
| 1,25 | 1,5 | 1,375 | 0,047851563 | -0,109375 | |||
| 1,375 | 1,5 | 1,4375 | -0,007263184 | 0,06640625 | |||
| 1,375 | 1,4375 | 1,40625 | 0,002456665 | -0,022460938 | |||
| 1,40625 | 1,4375 | 1,421875 | -0,000488043 | 0,021728516 | |||
| 1,40625 | 1,421875 | 1,414063 | 9,59635E-06 | -0,000427246 | |||
| 1,4140625 | 1,421875 | 1,417969 | -4,54392E-06 | 0,010635376 | |||
| 1,4140625 | 1,4179688 | 1,416016 | -2,17906E-06 | 0,00510025 | |||
| 1,4140625 | 1,4160156 | 1,415039 | -9,97854E-07 | 0,002335548 | |||
| 1,4140625 | 1,4150391 | 1,414551 | -4,07555E-07 | 0,000953913 | |||
| 1,4140625 | 1,4145508 | 1,414307 | -1,12483E-07 | 0,000263274 | Корень найден и равен1,4146 |
Задание 5. Решить уравнение 
:
1) В ячейку В1 Ввел погрешность нахождения корня 0,001;
2) За первоначальный отрезок локализации принял отрезок [0;2];
3) В ячейки C3, D3, E3, A4, B4, F4 ввел необходимые формулы;
4) Получил решение:
| Точность нахождения корня | 0,001 | ||||||
| a | b | c | Проверка знака | Значение функции в средней точке | |||
| =(A3+B3)/2 | =(A3^4-10)*(C3^4-10) | =C3^4-10 | |||||
| =ЕСЛИ(D3<=0;A3;C3) | =ЕСЛИ(D3<=0;C3;B3) | =(A4+B4)/2 | =(A4^4-10)*(C4^4-10) | =C4^4-10 | =ЕСЛИ(B3-A3<$B$1;"Корень найден и равен" &СТ(C3;"0?0000");"") | ||
| =ЕСЛИ(D4<=0;A4;C4) | =ЕСЛИ(D4<=0;C4;B4) | =(A5+B5)/2 | =(A5^4-10)*(C5^4-10) | =C5^4-10 | =ЕСЛИ(B4-A4<$B$1;"Корень найден и равен" &СТ(C4;"0?0000");"") | ||
| =ЕСЛИ(D5<=0;A5;C5) | =ЕСЛИ(D5<=0;C5;B5) | =(A6+B6)/2 | =(A6^4-10)*(C6^4-10) | =C6^4-10 | =ЕСЛИ(B5-A5<$B$1;"Корень найден и равен" &СТ(C5;"0?0000");"") | ||
| =ЕСЛИ(D6<=0;A6;C6) | =ЕСЛИ(D6<=0;C6;B6) | =(A7+B7)/2 | =(A7^4-10)*(C7^4-10) | =C7^4-10 | =ЕСЛИ(B6-A6<$B$1;"Корень найден и равен" &СТ(C6;"0?0000");"") | ||
| =ЕСЛИ(D7<=0;A7;C7) | =ЕСЛИ(D7<=0;C7;B7) | =(A8+B8)/2 | =(A8^4-10)*(C8^4-10) | =C8^4-10 | =ЕСЛИ(B7-A7<$B$1;"Корень найден и равен" &СТ(C7;"0?0000");"") | ||
| =ЕСЛИ(D8<=0;A8;C8) | =ЕСЛИ(D8<=0;C8;B8) | =(A9+B9)/2 | =(A9^4-10)*(C9^4-10) | =C9^4-10 | =ЕСЛИ(B8-A8<$B$1;"Корень найден и равен" &СТ(C8;"0?0000");"") | ||
| =ЕСЛИ(D9<=0;A9;C9) | =ЕСЛИ(D9<=0;C9;B9) | =(A10+B10)/2 | =(A10^4-10)*(C10^4-10) | =C10^4-10 | =ЕСЛИ(B9-A9<$B$1;"Корень найден и равен" &СТ(C9;"0?0000");"") | ||
| =ЕСЛИ(D10<=0;A10;C10) | =ЕСЛИ(D10<=0;C10;B10) | =(A11+B11)/2 | =(A11^4-10)*(C11^4-10) | =C11^4-10 | =ЕСЛИ(B10-A10<$B$1;"Корень найден и равен" &СТ(C10;"0?0000");"") | ||
| =ЕСЛИ(D11<=0;A11;C11) | =ЕСЛИ(D11<=0;C11;B11) | =(A12+B12)/2 | =(A12^4-10)*(C12^4-10) | =C12^4-10 | =ЕСЛИ(B11-A11<$B$1;"Корень найден и равен" &СТ(C11;"0?0000");"") | ||
| =ЕСЛИ(D12<=0;A12;C12) | =ЕСЛИ(D12<=0;C12;B12) | =(A13+B13)/2 | =(A13^4-10)*(C13^4-10) | =C13^4-10 | =ЕСЛИ(B12-A12<$B$1;"Корень найден и равен" &СТ(C12;"0?0000");"") | ||
| =ЕСЛИ(D13<=0;A13;C13) | =ЕСЛИ(D13<=0;C13;B13) | =(A14+B14)/2 | =(A14^4-10)*(C14^4-10) | =C14^4-10 | =ЕСЛИ(B13-A13<$B$1;"Корень найден и равен" &СТ(C13;"0?0000");"") | ||
| =ЕСЛИ(D14<=0;A14;C14) | =ЕСЛИ(D14<=0;C14;B14) | =(A15+B15)/2 | =(A15^4-10)*(C15^4-10) | =C15^4-10 | =ЕСЛИ(B14-A14<$B$1;"Корень найден и равен" &ТЕКСТ(C14; "0,0000");" ") |
| Точность нахождения корня | 0,001 | ||||||
| a | b | c | Проверка знака | Значение функции в средней точке | |||
| -9 | |||||||
| 1,5 | 44,4375 | -4,9375 | |||||
| 1,5 | 1,75 | 3,06665 | -0,62109 | ||||
| 1,75 | 1,875 | -1,46554 | 2,359619 | ||||
| 1,75 | 1,875 | 1,8125 | -0,49206 | 0,792252 | |||
| 1,75 | 1,8125 | 1,78125 | -0,04161 | 0,066987 | |||
| 1,75 | 1,78125 | 1,765625 | 0,174912 | -0,28162 | |||
| 1,765625 | 1,78125 | 1,773438 | 0,030547 | -0,10847 | |||
| 1,773438 | 1,78125 | 1,777344 | 0,002281 | -0,02103 | |||
| 1,777344 | 1,78125 | 1,779297 | -0,00048 | 0,022906 | |||
| 1,777344 | 1,779297 | 1,77832 | -1,9E-05 | 0,00092 | |||
| 1,777344 | 1,77832 | 1,777832 | 0,000212 | -0,01006 | |||
| 1,777832 | 1,77832 | 1,778076 | 4,6E-05 | -0,00457 | Корень найден и равен1,7778 |
Список литературы:
· Информатика. Базовый курс. 2-е издание / Под ред. С.В. Симоновича. – СПб.: Питер,2006. – 640 с.: ил. ISBN 5-94723-752-0
· Информатика. Базовый курс С. В. Симонович и др. – СПб.: Питер. 2006 – 640 с. ISBN 5-8046-0134-2
· Могилев А. В. Информатика. Учебное пособие для студентов педагогических ВУЗ-ов./А.В. Могилев, Н.И. Пак, Е.К. Хённер; Под Ред. Е.К. Хённер – 3-е изд. перераб. 4 доп. – М.: Издательский центр «Академия», 2004.-848 с. ISBN 5-7695-1709-3
· Тихомиров А.Н., Прокди А.К., Колосков П.В.,Клеандрова И.А. и др..
MICROSOFT OFFICE 2007, Все программы пакета: WORD, EXCEL, ACCESS,POWERPOINT, PUBLISHER, OULOOK, ONENOTE, INFOPATH, GROOVE. Самоучитель –СПб.: Наука и Техника, 2008. – 608 с.: ил.+ цв. вклейки.